機械設計をする上で摩耗(Wear)は悩ましい問題の一つです。
摩擦摩耗試験などの基礎試験を行うと分かりますが、一般に摩耗量は温度に依存しますので、摩耗現象の解明には温度を計算できると便利なことも多いです。
本記事では摩擦面(摺動面, すべり面)の温度を計算する方法について解説します。
固体表面の接触
固体表面は機械加工など様々な方法で作られますが、微視的に見ると必ず凹凸(表面粗さ)が存在します。
2つの部品間で実際に接触し、荷重が伝達される部位はその凹凸の凸部付近になります。
このような部分を真実接触点(Real contact point)と言い、その真実接触点の面積を合計したものを真実接触面積(Real contact area)と言います。
反対にCADで描いたときのような幾何学的な形状により決まる投影面積を見かけの接触面積(Apparent contact area)と言います。
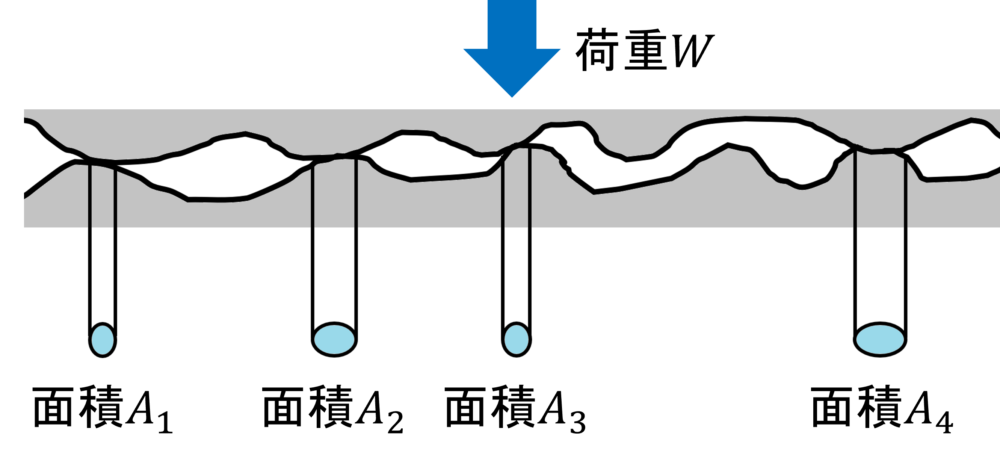
よって、真実接触点が見かけの接触面積内に\(n\)個ある場合、真実接触面積\(A \, (m^2)\)は下式で求められます。
粗さをもつ面同士を接触されると微小な複数の接触点が発生しますが、荷重を印加していくと最初は弾性変形が発生します。
そこから更に荷重\(W \, (N)\)を増やすと塑性流動圧力\(p_m \, (Pa)\)に達し、塑性変形領域へ移行します。そのときの真実接触面積\(A\)は下式より求められます。
なお、塑性流動圧力\(p_m\)は材料のビッカース硬さ\(H\)に相当し、実験によれば単純引張りの降伏応力\(\sigma_y\)と次の関係があります。
ビッカース硬度 Hv250の場合の塑性流動圧力\(p_m\)は
\(Hv250 \, kgf/mm^2 = 250 \times 9.8 \times 10^6 \simeq 2.45 \times 10^9 \, Pa\)
となるね。
摩擦面の温度
2つの部品間で摺動させると摩擦仕事が発生し、その大部分は熱に変換され、温度上昇が発生します。
真実接触面積は非常に小さいため、閃光温度(Flash temperature)と呼ばれる瞬間的な高温が発生します。
閃光温度\(\Delta T \, (deg\,C)\)は、摩擦係数を\(\mu\)、接触荷重を\(W\,(N)\)、摺動速度を\(v\,(m/s)\)、仕事の熱当量を\(J \,(J/cal)\)、熱伝導率を\(k_1 , k_2 \, (W/(m \cdot K))\)、接触面の半径を\(r \, (m)\)とすると下式で求められます。
(参考文献:E. Rabinowicz,Friction and Wear of Materials,1965)
なお、接触面の半径\(r\)は式(2)より、下式で求められます。
まとめ
本記事では真実接触点での温度の計算方法について解説しました。
その過程にて真実接触面積の計算方法も示しましたが、CADで描いたような幾何学的に綺麗な平面 又は 曲面同士の接触面積について求めたい場合もあります。
以下の記事にて解説しているので、併せて読んでみて頂ければと思います。
また、摩擦・摩耗・潤滑を扱う学問をトライボロジー(Tribology)と言いますが、体系的に学ぶには書籍が一番コスパが高いです。抱えている課題に真剣に向き合いたいと感じる方は書籍でも学習してみることをおすすめします。




