自動車などの耐振性が求められる製品では、必ず振動試験が行われます。
この振動試験にはサイン波振動試験、ランダム波振動試験、実時間波形試験、衝撃試験があります。
サイン波振動試験はサイン波の加速度を与える試験ですが、これは更に振動数(周波数)を固定するものと振動数を可変するものがあります。
本記事では周波数を決められた時間内で可変する振動数掃引について解説します。
振動数掃引とは
振動数とは1秒あたりに繰り返される波の回数のことを言い、単位はHz(ヘルツ)を使います。
振動数掃引とは、振動数をある時間内で徐々に変えていくことを言います。
(例えば10Hz ~ 1000Hzまでを連続的に5分で上げていく、など)
この振動数の変え方には以下の二つがあります。
- 直線掃引(リニアスイープ)
時間の経過に比例して一定の割合で振動数を変えていく方法です。
この方法は振動数が少ないときは時間内の振動回数は少ないですが、掃引し振動数が上がっていくと時間内の振動回数が増えていきますので、振動数ごとで不均一が発生してしまいます。 - 対数掃引(ログスイープ)
低い振動数のときはゆっくり振動数を変えていき、高い振動数の場合は速く振動数を変える方法です。
この方法は各振動数で振動回数は一定になります。
対数掃引の式
対数掃引(ログスイープ)は、fig. 1のように時間\(t\)を横軸(リニアスケール)、振動数\(f\)を縦軸(ログスケール)としたときに片対数グラフ上で直線となるようする方法です。
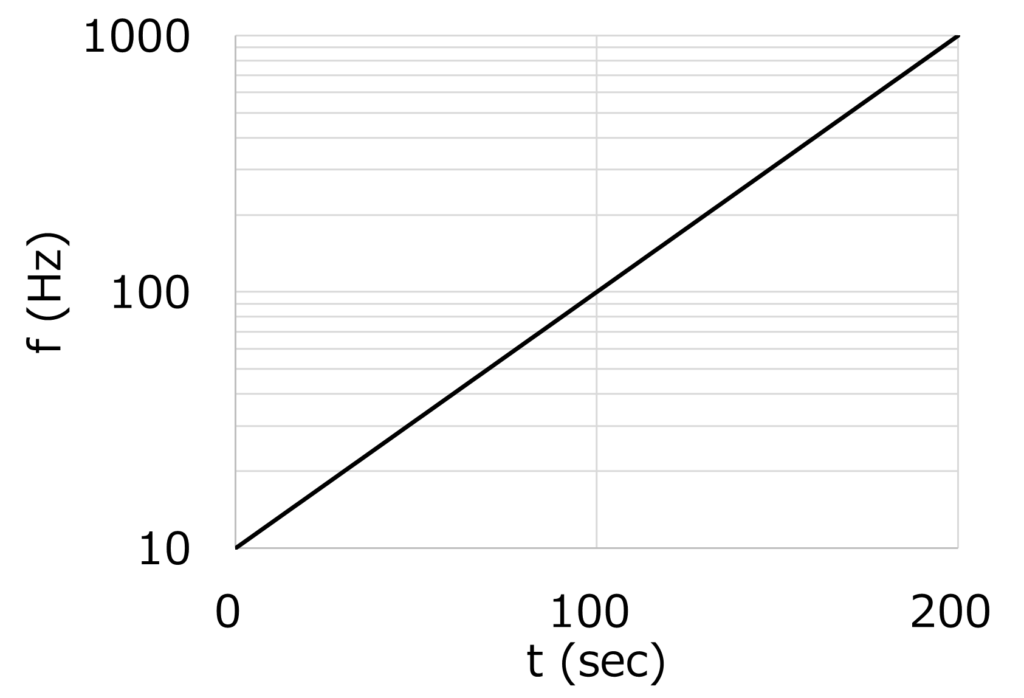
ここでは、Fig. 1を例に対数掃引の場合の振動数を求める式について考えていきます。
本例は\((0, \, 10)\)と\((200, \, 1000)\)を通る直線のグラフになっています。
①.まず、片対数グラフ上での傾き\(a\)を求めます。
②.次に 片対数グラフ上での切片\(b\)を求めます。
③.傾き\(a\)と切片\(b\)から片対数グラフ上での直線の式\(at + b\)を求めます。
④.対数と指数の性質から\(f\)を求める式に変形します。
式(4)をグラフ化したものがfig. 1になります。なお、fig. 1は片対数グラフですが、縦軸もリニアスケールにしたグラフを参考に示します。
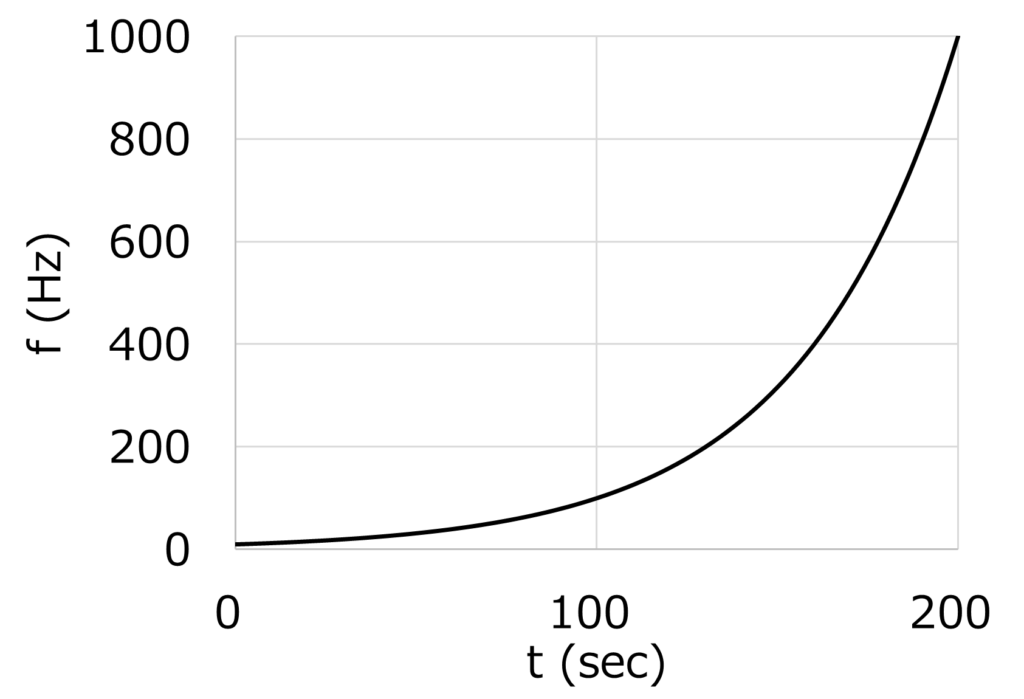
振動数が高い領域は時間が少なくなっており、振動数ごとの実際の振動回数の不均一さが直線掃引に比べて改善されていることが分かります。





