昨今ではロボットや自動車の進歩により、各機構を動かすアクチュエータとしてDCモータがますます使われるようになってきました。
DCモータを組み込んだ装置(製品)のプラントモデルや制御モデルを作る際は、数理式を立ててモデル化したい場面が多いかと思います。
本記事ではDCモータの基礎から理解するために回転原理から解説し、実際にMATLAB/Simulinkでモデル化し、作成したモデルの動作検証方法までを解説します。
DCモータの基礎知識
数理式に入る前に基礎知識として、DCモータの回転原理から見ていきたいと思います。
フレミングの左手の法則
フレミング左手の法則(Fleming’s left hand rule)は中学二年生で習いましたが、一度おさらいしてみたいと思います。

フレミング左手の法則はジョン・フレミングが考案した暗記法で、磁界の中で導体に電流が流れたとき、その導体にかかる力の向きを示すものです。この力は、ローレンツ力(Lorentz force)とも呼ばれます。
ここで、磁界の強さを\(B\) (単位:\(T\))、導体の長さを\(L\) (単位:\(m\))、電流を\(I\) (単位:\(A\))と置くと、導体に働く力\(F\) (単位:\(N\))は下式で表されます。
DCモータの回転原理
フレミング左手の法則をおさらいしたところで、DCモータの回転原理について見ていきましょう。
下図では磁石により磁界\(B\)が発生し、コイル(導体)に電流\(I\)が流れることでコイルを回転させようとする力\(F\)が生まれます。これによりトルク\(T\) (単位:\(N \cdot m\))が発生し、下図の例ではモータは時計回りに回転します。
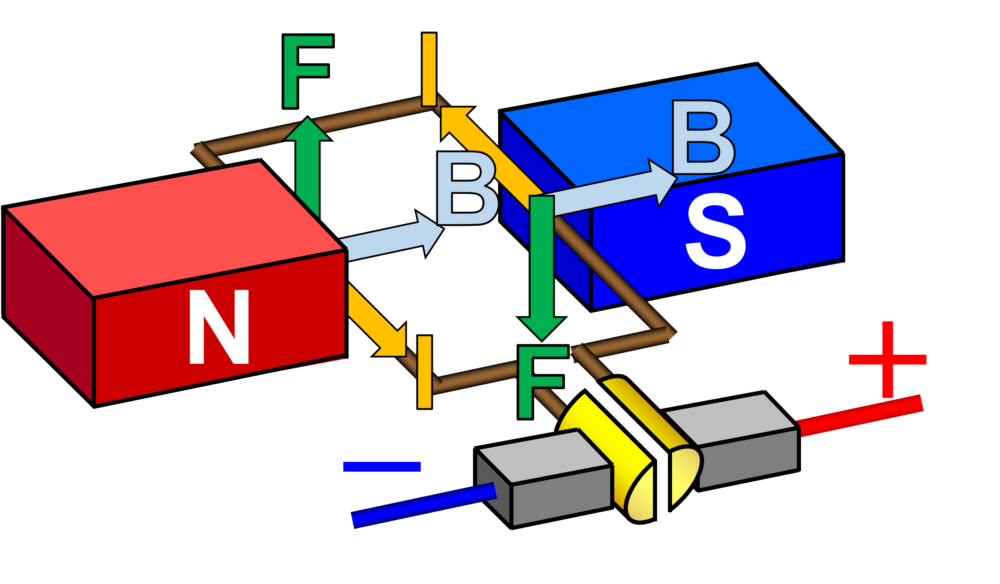
ここで、モータのコイルより発生するトルクを\(T_{gen}\)と置くと、電流\(i\)との関係は下式のように表されます。
このトルクと電流を結ぶ比例定数\(K_T\)はトルク定数と呼ばれます。
なお、単位は\(N \cdot m/A\)となります。
DCモータの発電作用
上記は外部から電圧を印加し、コイルに電流を流した場合を考えました。今度は同じ装置(モータ)に外部から動力を与えて回転させたらどうなるでしょうか。
答えは発電機として振る舞うが正解です。
モータの端子間に何も接続されていない状態(解放状態)にて回転速度\(\omega\) (単位:\(rad/s\))で回転させたとき、モータの端子間に現れる電圧\(E_{bef}\) (単位:\(V\))は下式で表されます。
この電圧は逆起電力とも呼ばれ、逆起電力と回転速度を結ぶ比例定数\(K_E\)は逆起電力定数と呼ばれます。
なお、単位は\(V/(rad/s)\)となります。
回転速度(回転数)の単位はSI単位系ではないけど\(rpm\)がよく用いられるね。\(rad/s\)に直すには\(\pi/30\) 倍すればよいよ!
【例】\(3000 \, (rpm) \times \frac{\pi}{30} \approx 314 \, (rad/s)\)
DCモータの数理式
上記の基礎知識をもとに、DCモータの数理式について考えていきましょう。
DCモータの等価回路
モータはコイルで構成されており、一種の電気回路となっています。
電気回路の世界では、電圧と電流の関係が等しくなる回路を等価回路と呼びますが、モータの電気的な応答を簡単化して考えるために本記事でも等価回路で考えてみます。
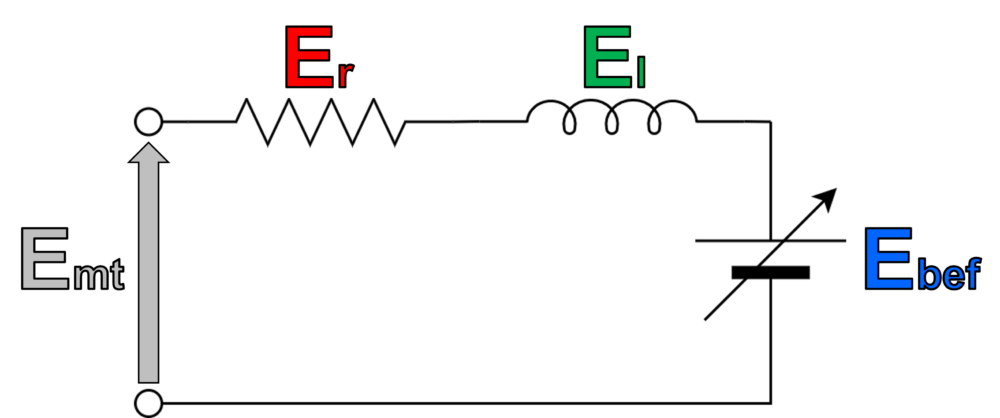
コイルの持つ抵抗による電圧降下を\(E_r\)、インダクタンスによる電圧降下を\(E_l\)、逆起電力を\(E_{bef}\)、モータの端子間電圧を\(E_{mt}\)と置くと、DCモータの等価回路は上図のようになります。
上図の回路について考えてみますが、電気回路を解析する際に重要な法則にキルヒホッフの法則いうものがあります。
- キルヒホッフの第1法則(Kirchhoff’s Current Law)
回路中の任意の分岐点において、流入する電流と流出する電流の総和は等しい。 - キルヒホッフの第2法則(Kirchhoff’s Voltage Law)
回路の任意の一回りの閉じた経路において、起電力の総和と電圧降下の総和は等しい。
キルヒホッフの第2法則を用いると、各電圧の関係は下式で表されます。
ここで、回路に流れる電流を\(i\)、コイルの抵抗を\(R\) (単位:\(\Omega\))と置くと、オームの法則より式(4)は下式で表されます。
コイルは抵抗成分の他にインダクタンス成分を持ちます。これは、電流が早く変化した際に抵抗が大きくなる性質のことです。
よく子供に「クルマは急には止まれないから、道路を横断するときは左右をよく見てね!」と言いますよね。これは、クルマの質量は大きいので大きな慣性力を持つためです。
電気の世界にも慣性のようなものがあり、それがインダクタンスになります。
コイルのインダクタンスを\(L\) (単位:\(H\))、時間を\(t\) (単位:\(s\))と置くと、式(5)は以下のような常微分方程式で表すことができます。
さらに、式(6)に式(3)を代入すると以下のようになります。
電気回路について自信がない方は、以下の書籍を見ると分かりやすいです。
電気は目に見えないため分かりにくいところもありますが電流を水流に例えてイメージしやすくしたり、絵をふんだんに使って解説されており、ほぼ中学レベルの知識で読むことができます。
入門書ですが、教科書と違って実務知識も掲載されており、周りと差をつけたい方はおすすめです。
DCモータの運動方程式
高校から大学初年度にかけて物理の授業でニュートンの運動方程式を習います。これは印加される力が既知であれば物体の位置や速度が解ける、つまり “運動が解ける方程式” でした。
質量を\(m\) (単位:\(kg\))、速度を\(v\) (単位:\(m/s\))、力を\(F\) (単位:\(N\))と置くと、ニュートンの運動方程式は下式で表されます。
ところで、式(8)は並進運動系の運動方程式です。しかし、モータは回転運動をしています。
慣性モーメントを\(J\) (単位:\(kg \cdot m^2\))、回転速度(角速度)を\(\omega\) (単位:\(rad/s\))、トルクを\(T\) (単位:\(N \cdot m\))と置くと、回転運動系の運動方程式は下式で表されます。
よって、モータの運動方程式は、回転するコイル部分(回転子:Rotor)の慣性モーメントを\(J_{rt}\)、そのトルクを\(T_{rt}\)と置くと、以下のように表されます。
モータの回転速度が上昇するときは、慣性力として\(T_{rt}\)分だけ負荷となるよ。
DCモータの損失
モータは電気エネルギーを運動エネルギーに変換する装置ですが、効率100%という訳には勿論いきません。
本記事ではモータを設計する立場ではなく、モータを使う立場として簡易的なモデル化を目指します。もし、モータの損失に関してご興味のある方は、JSOL殿の記事が参考になるかと思います。
はじめに・第1話:損失の分類
https://www.jmag-international.com/jp/loss_analysis/01/
さて、モータの損失としては回転速度に依存する成分が多くを占めます。この成分による損失トルク\(T_d\)は粘性抵抗係数\(D\) (単位:\(N \cdot m/(rad/s)\))を比例定数とし、下式のように表されます。
DCモータのトルクの関係式
ここで、回転子を回すトルク\(T_{rt}\)を求めます。
外部負荷による負荷トルクを\(T_{mt}\)と置くと、下式のようになります。
よって、式(12)に式(2)、(10)、(11)を代入すると以下のようになります。
DCモータの数理式 まとめ
以上より、DCモータの数理式は下式のようになります。
Simulinkによるモデル化
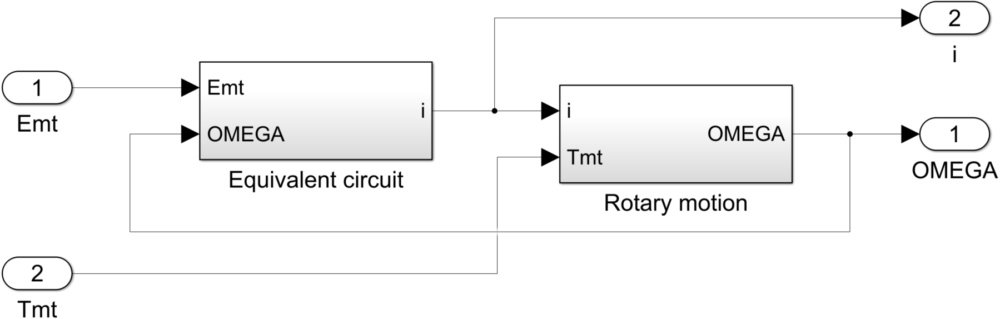
本記事では、以下のような入出力をもつモデルを作成します。

mファイルの作成
本記事では例題として、マブチモータ製の小型モータ(RE-260RA-2295)をモデル化したいと思います。
最初に各パラメータを算出しますが、トルク定数、逆起電力定数、抵抗と粘性抵抗係数はカタログより同定します。また、インダクタンスと慣性モーメントは沼津高専 伏見氏らの論文を参考にさせて頂きました。
| 項目 | 値 | 単位 |
|---|---|---|
| トルク定数 \(K_T\) | \(2.54 \times 10^{-3}\) | \(N \cdot m/A\) |
| 逆起電力定数 \(K_E\) | \(2.88 \times 10^{-3}\) | \(V/(rad/s)\) |
| 抵抗 \(R\) | \(1.11\) | \(\Omega\) |
| インダクタンス \(L\) | \(1.4 \times 10^{-4}\) | \(H\) |
| 慣性モーメント \(J_{mt}\) | \(1.4 \times 10^{-5}\) | \(kg \cdot m^2\) |
| 粘性抵抗係数 \(D\) | \(4 \times 10^{-7}\) | \(N \cdot m/(rad/s)\) |
次に、Table 1のパラメータ、印加電圧と負荷トルクを設定するために、以下のようなスプリクト(mファイル)を作成します。
clear; clc;
Kt = 2.54 * 10^-3; % トルク定数 [N-m/A]
Ke = 2.88 * 10^-3; % 逆起電力定数 [V/(rad/s)]
R = 1.11; % 抵抗 [ohm]
L = 1.4 * 10^-4; % インダクタンス [H]
Jrt = 1.4 * 10^-5; % 慣性モーメント [kg-m^2]
D = 4 * 10^-7; % 粘性抵抗係数 [N-m/(rad/s)]
Emt = 1; % モータの端子間電圧 [V]
Tmt = 0; % 負荷トルク [N-m]
sim('MotorModel.slx');次のパートでSimulinkモデルを作成しますが、上記の例では ‘MotorModel.slx’ というファイル名にしました。
Simulinkでのブロックの配置
まずは上で導出した式(7)をSimulink用いてモデル化していきます。
各項を移項して整理すると以下のようになります。
ここでは、「Equivalent circuit」という名前のサブシステムを作成し、式(15)をSimulinkモデルにします。Simulinkモデル化したものを下図に示します。
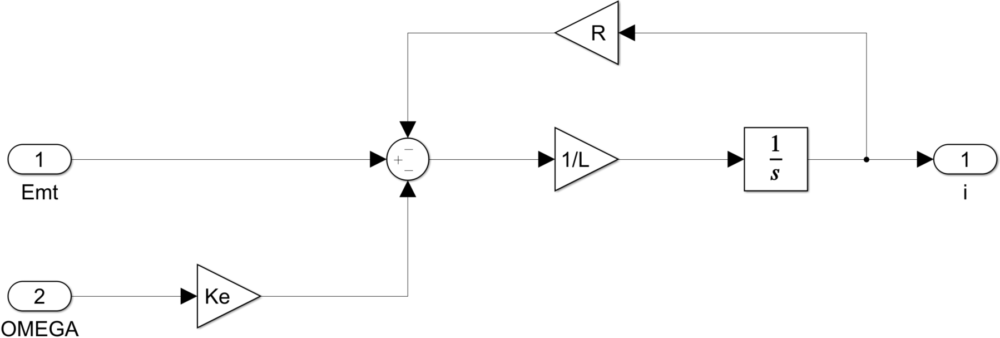
もし、初期(\(t=0\))の電流\(i_0\)がゼロでないときは、Integratorブロックをダブルクリックし設定します。
初期条件を設定する場合は、ブロックパラメータウィンドウの「初期条件のソース」を「外部」に変更するとブロック図上で設定できるため、モデルの可読性があがるよ!
同様に上で導出した式(13)をSimulink用いてモデル化していきます。
各項を移項して整理すると以下のようになります。
「Rotary motion」という名前のサブシステムを作成し、式(17)をSimulinkモデルにします。Simulinkモデル化したものを下図に示します。
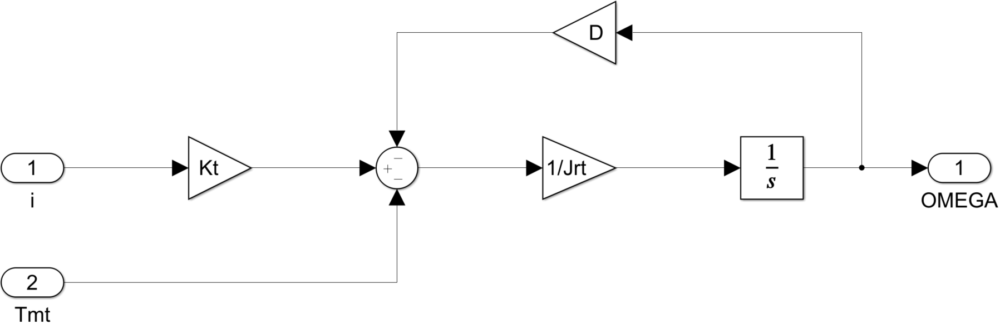
もし、初期(\(t=0\))の角速度\(\omega_0\)がゼロでないときは、Integratorブロックをダブルクリックし設定します。
ここでは、先ほど作成したサブシステム同士を接続(リンク)させるだけです。下図のように「DC motor」という名前のサブシステムを作成します。
MATLABについて勉強されたい方は以下の書籍を手元に置いておくと便利です。
MATLABのスクリプトの書き方、Simulinkの使い方など基本的なことは全て載っています。インターネットで調べるのもよいですが、紙ベースだと一覧性があり調べるのも楽です。
モデルの動作検証
モデルの作成が終わったら動作検証が必要です。以下のように、スクリプトで設定した端子間電圧と負荷トルクの値を代入し、Workspaceへ格納するモデルを作成します。

まずは、mファイルの設定は変えずに実行してみましょう。そして、Workspaceへ出力されたデータをExcelにて下図のようにグラフ化してみます。(Fig. 8のモデルは回転速度の単位をrpmにしていますが、rpsに直してグラフ化しています)
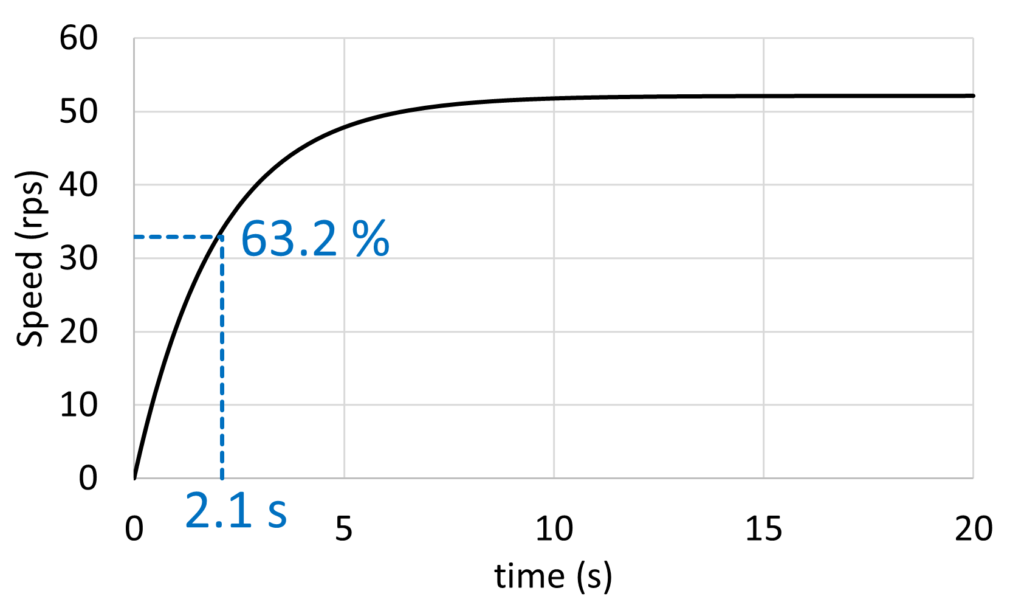
上図は負荷トルクはゼロ、電圧に1Vを加えたときのステップ応答のグラフになっています。
ここで、先ほどの沼津高専 伏見氏らの論文を見ていると2.1sで定常回転速度の63.2%にきていますので、応答速度(時定数)は正しく再現できていることが確認できまます。
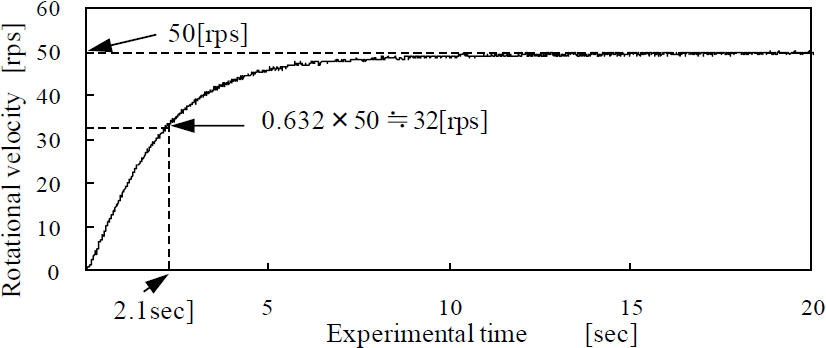
[引用:伏見氏ら, 安価に製作できる簡易型DCモータ制御学習教材の開発]
次に、トルク vs. 回転速度, 電流特性(TNI特性)を確認してみましょう。
mファイルの端子間電圧\(E_{mt}\)を3 Vへ変更し、負荷トルク\(T_{mt}\)はマブチモータ殿のカタログの測定点である無負荷点、最大効率点、停動点の3点を計算します。(面倒な方はRampブロックを使用しましょう)
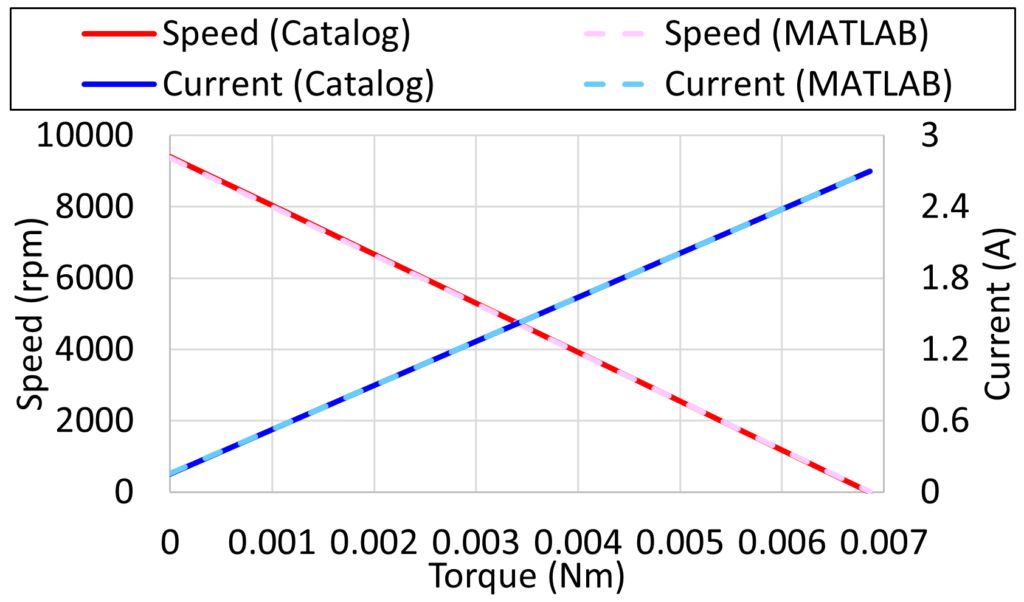
Excelにてデータをまとめると、上図のようにTNI特性も正しく再現できていることが確認できまます。
まとめ
今回はDCモータの回転原理から解説し、MATLAB/Simulinkでのモデル作成・動作検証の方法までを解説しました。
今回のモデルでは方程式を一つ一つモデル化しシリアルに接続してSimulinkで解く方法を紹介しましたが、次回は行列を用いてシンプルにモデル化する方法について解説します。
なお、本記事ではDCモータの詳しい構造や原理について紹介しませんでしたが、実際にモータを使いこなすには実物をよく理解していることが重要です。
DCモータの基本構造、基本原理、等価回路、計測や特性調整、制御システム、電磁界理論、放熱などに関して知りたい方は以下の書籍が参考になるかと思います。
また、DCモータに限らず、モータ全般的な知識について学びたい方は以下の書籍が参考になります。写真や図がふんだんに使われており見ていて楽しいですし、初学者にも大変分かりやすく書かれています。
また、モータについて詳しい方でも、モータのついて詳しくない方に上手く説明したい場面もあるかと思います。資料作成の際の参考資料としても手元に置いておきたい一冊です。





