本記事は「基礎から学ぶDCモータの1Dモデル化 ~MATLAB/Simulink~」の2回目です。
前回の記事ではフレミング左手の法則について復習し、DCモータの回転原理について解説してそれを数理式(数理モデル)に置き換えてMATLAB/Simlinkでモデル化する方法を紹介しました。
DCモータの数理式は線形の微分方程式ですので、行列を用いるとシンプルに記述することができます。また、行列を用いて各状態量のつり合いを取りながら解くことで数値計算の精度向上も期待できます。(力のつり合い計算への応用等で有用)
本記事では、DCモータの1Dモデルを現代制御理論の分野で用いる状態方程式に直すことで、MATLAB/Simlinkのモデルをシンプルに記述する方法について解説します。
本記事はこちらの記事の続きとなります。
制御理論の概要
DCモータを1Dモデル化する目的としては、以下のものが考えられるかと思います。
- ロボットなどでアクチュエータとして使われているDCモータを制御する制御モデルを構築したい。
- モデルベース開発(MBD)による開発効率向上のため、プラントモデルを構築したい。
どちらの場合においても、MATLABでモデル化をするときは制御理論(Control theory)が基礎になりますので押さえておく必要があります。
ここで制御とは、対象を希望通りに「制(せい)し、御(ぎょ)する」ことを言い、電流・電圧・変位・速度・加速度などの物理量を目標値(希望する値)に一致させる操作のことを言います。
- 制 勝手なふるまいを押さえる
- 御 思うように操る
なお、制御モデルとプラントモデルの違いについては、以下の記事をご覧ください。
制御理論の歴史
制御理論には大きく分けて古典制御理論(Classical control theory)と現代制御理論(Modern control theory)の2種類があります。
古典制御理論は18世紀後半に、蒸気機関の回転速度を一定にするためにジェームズ・ワットが実用化した遠心調速機が始まりとされています。
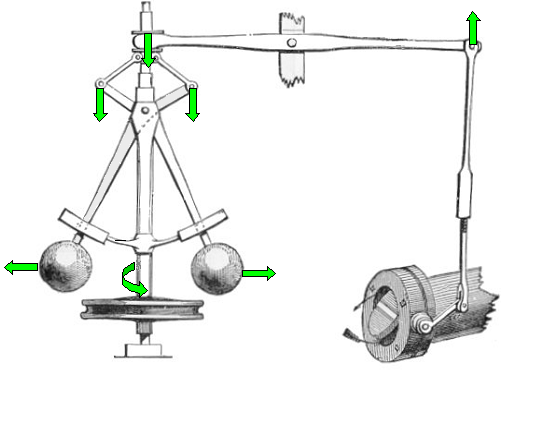
それから理論的研究が進んでいき、古典制御理論は1950年代ごろに確立していきました。
1950年代に入ると第二次世界大戦で戦勝国となったアメリカとソ連は宇宙開発競争でしのぎを削ります。
ロケットを制御するときに位置や姿勢の測定にはセンサーが用いられますが、センサーの値はノイズだらけです。その値をそのまま用いると、宇宙飛行のような長距離移動では誤差が蓄積していき、目的地にたどり着くことは到底できません。
しかし、1960年になるとそうしたノイズをキャンセルするカルマンフィルタ(Kalman filter)が発明されます。これにより、1969年7月20日にアポロ11号は人類初の月面着陸に成功します。

アポロ・ガイダンス・コンピュータ(AGC)
カルマンはたくさんの現代制御理論の重要な論文を発表し、現代制御理論の基本的な枠組みをほとんど1人で作り上げました。そのため、カルマンは「現代制御理論の父」と呼ばれています。
古典制御理論と現代制御理論
数理モデルの表現には伝達関数表現と状態空間表現があります。
伝達関数とは、入出力を表す関数におけるすべての変数の初期値がゼロであるとして、ラプラス変換したときの入力と出力の比のことを言います。
出力を\(y(t)\)のラプラス変換を\(Y(s)\)、入力\(u(t)\)のラプラス変換を\(U(s)\)とすると伝達関数\(G(s)\)は下式で表されます。
よって、伝達関数表現は下図のように入力変数\(U(s)\)から直接、出力変数\(Y(s)\)へ影響を与える式で表されます。
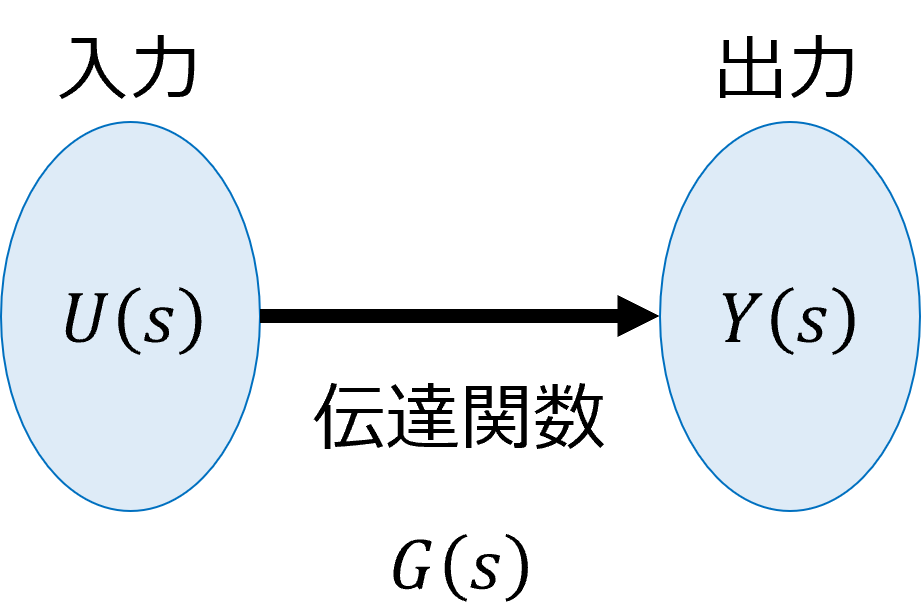
これに対し、状態空間表現は入力変数\(\boldsymbol{u}(t)\)から状態変数\(\boldsymbol{x}(t)\)までの影響を状態方程式で表し、その後、状態変数\(\boldsymbol{x}(t)\)と出力変数\(\boldsymbol{y}(t)\)とのつながりを出力方程式で表す方法となります。

古典制御理論では伝達関数表現を用い、現代制御理論では状態空間表現を用います。これにより古典制御理論では1入力1出力システム(SISOシステム)が基本となります。
現代制御理論では行列やベクトルを用いた式を使うことで、多入力多出力システム(MIMOシステム)を扱うことができます。
状態空間表現を用いたDCモータの1Dモデル化
では、前回の記事で導出した数理式をもとに、実際に状態方程式と出力方程式を求めたいと思います。
今回は例題として、電圧\(E_{mt}\)と負荷トルク\(T_{mt}\)を入力とし、電流\(i\)を出力とするモデルを作成したいと思います。
本記事では線形代数の慣例に従って、小文字で太字の量記号をベクトル、大文字の量記号を行列とするよ。
状態方程式の導出
モータの端子間電圧を\(E_{mt}\)、電流を\(i\)、コイルの抵抗を\(R\)、インダクタンスを\(L\)、逆起電力定数を\(K_E\)、トルク定数を\(K_T\)、慣性モーメントを\(J_{rt}\)、回転速度を\(\omega\)、粘性抵抗係数を\(D\)、負荷トルクを\(T_{mt}\)、時間を\(t\)と置くと、DCモータの数理式は以下の通りでした。
ここでは、Fig. 4で示したように下式のような状態方程式へ変換します。
入力変数\(\boldsymbol{u}\)(ベクトル)の成分を\(E_{mt}\)と\(T_{mt}\)とすると
また、現代制御理論にて状態変数と呼ばれる内部変数\(\boldsymbol{x}\)(ベクトル)の成分を\(i\)と\(\omega\)とすると
以上の変数の定義を頭に入れながら、式(2)、(3)を式変形すると
式(7)、(8)を行列の形で書くと
よって、状態方程式の行列\(A\)と\(B\)は以下のようになります。
出力方程式の導出
下図のような状態変数\(\boldsymbol{x}\)の成分である電流\(i\)を出力とする出力方程式を求めます。
よって、出力方程式のベクトル\(\boldsymbol{c}\)は以下のようになります。
mファイルの作成
前回の記事で作成したmファイルをベースに行列\(A\)、\(B\)とベクトル\(\boldsymbol{c}\)を追加します。
追加分は13~19行目になります。今回はカタログ(RE-260RA-2295)に記載のある\(3\,V\)印加時の最大効率点(\(1.31 \, mN \cdot m\))の電流を計算するために、10~11行目も変更しました。
clear; clc;
Kt = 2.54 * 10^-3; % トルク定数 [N-m/A]
Ke = 2.88 * 10^-3; % 逆起電力定数 [V/(rad/s)]
R = 1.11; % 抵抗 [ohm]
L = 1.4 * 10^-4; % インダクタンス [H]
Jrt = 1.4 * 10^-5; % 慣性モーメント [kg-m^2]
D = 4 * 10^-7; % 粘性抵抗係数 [N-m/(rad/s)]
Emt = 3; % モータの端子間電圧 [V]
Tmt = 1.31 * 10^-3; % 負荷トルク [N-m]
% 状態方程式
A = [-R/L -Ke/L ;
Kt/Jrt -D/Jrt];
B = [1/L 0 ;
0 -1/Jrt];
% 出力方程式
c = [1 0];
sim('MotorModel.slx');Simulinkでのブロックの配置
次はSimulinkにてブロックを配置していきます。式(4)は微分形になっていますので積分形に直した下式を用います。
(もし、初期値を入れる場合はIntegrator Blockの設定をします)
電流の値を出力するために、式(12)の出力関数を使用します。下図がMATLAB/Simulinkにてモデル化したものになります。
(Matrix Multiply Blockではベクトル同士の掛け算はできないので注意してください。)
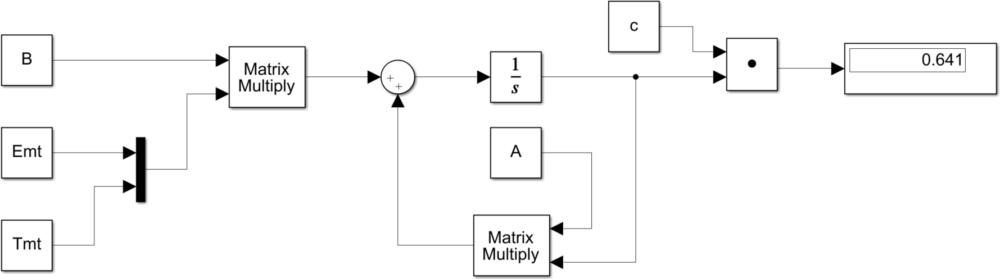
Fig. 5は実際に実行した結果を示しています。カタログ値は0.64Aですので正しく計算できていることがわかります。
過渡応答など、動作検証をもう少し真面目にやりたい人は下のリンクの記事を参考にしてみてね!
まとめ
今回は行列を用いることでモデルをシンプルに記述する方法について解説しました。
もし、MATLAB\Simulinkのブロックにて行列を計算するやり方に自信がない方はこちらの記事を参考にしてみてください。
また、現代制御理論に興味がある方はこちらの書籍が参考になるかと思います。
現代制御理論の教科書の多くは、理論や法則、設計手順などを一般化し、その証明に多くのページが割かれていますが、「わかりやすい 現代制御理論」では内容を絞ることで丁寧に解説されていますので、挫折が少なくなるようになっています。
また、演習問題として倒立振子も取り扱っており、理解を助けるようになっています。
現代制御理論を用いて実際にMATLAB/Simulinkでモデルを作成するとき、作成の過程でちょっとしたことかも知れませんがつまづく場合があります。
「MATLAB/Simulinkによる現代制御理論」は現代制御理論とMATLAB/Simulinkを連携させて解説がされた数少ない書籍です。基本操作も解説されており、MATLAB/Simulinkと現代制御理論の両方を学びはじめた方には特におすすめの一冊です。







