本頁ではステンレス鋼(SUS316L)の応力ひずみ線図(S-Sカーブ)について扱います。
圧入(Interference fit)などの一部の機械要素は塑性域の挙動が重要になりますので、構造解析(CAE)で計算する際に必要な情報になります。
材料の組成
SUS316Lのテストピースの組成は以下のようになります。
| 材料 | C | Si | Mn | Cr | Mo | Ni |
| SUS316L | 0.03 | 1.0 | 2.0 | 16.5 | 2.0 | 11.0 |
応力ひずみ線図
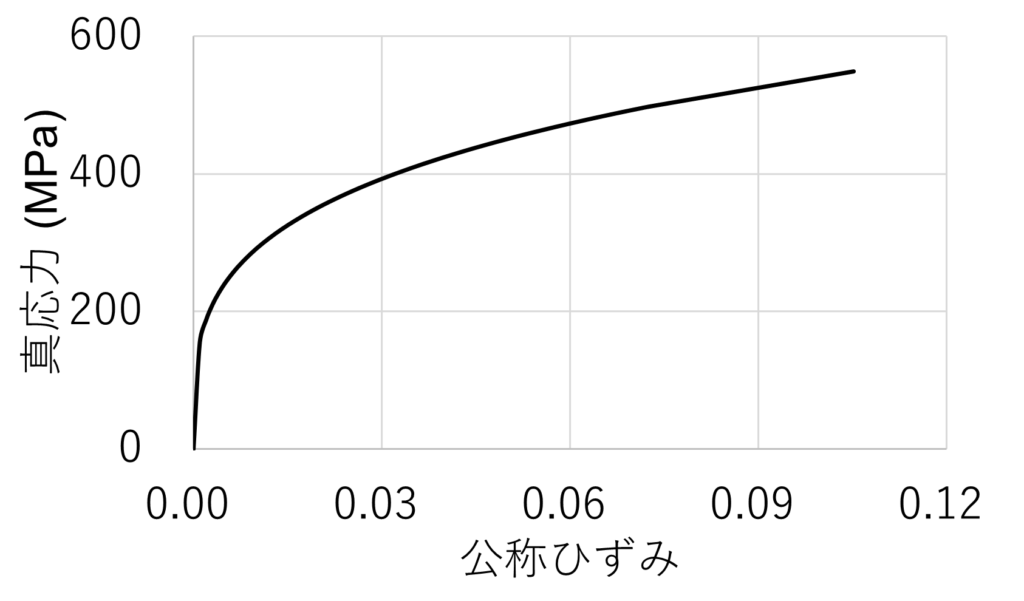
SUS316Lの応力ひずみ線図を以下に示します。
(出展:Stavros Syngellakis氏ら, Finite element simulation of spherical indentation experiments)
なお、真応力を\sigma_{t}、公称応力を\sigma_{e}、真ひずみを\varepsilon_{t}、公称ひずみを\varepsilon_{e}とおくと、下式のように変換できます。
\begin{eqnarray}
\sigma_t=\sigma_e(1+\varepsilon_e) \tag{1}\\
\\
\varepsilon_t=\ln(1+\varepsilon_e) \tag{2}
\end{eqnarray}
カヲル
構造解析ソフトによって真応力なのか公称応力なのか、真ひずみなのか公称ひずみなのか異なるので、そのソフトのオンラインヘルプなどで必ず確認してね。
最後にFig. 1のテーブルデータも示しておきます。
| 公称ひずみ (-) | 真応力 (MPa) |
|---|---|
| 0 | 0 |
| 0.001 | 155 |
| 0.002 | 187 |
| 0.003 | 209 |
| 0.004 | 227 |
| 0.005 | 241 |
| 0.006 | 253 |
| 0.007 | 264 |
| 0.008 | 274 |
| 0.009 | 283 |
| 0.010 | 291 |
| 0.011 | 299 |
| 0.012 | 306 |
| 0.013 | 313 |
| 0.014 | 320 |
| 0.015 | 326 |
| 0.016 | 332 |
| 0.017 | 337 |
| 0.018 | 343 |
| 0.019 | 348 |
| 0.020 | 353 |
| 0.021 | 357 |
| 0.022 | 362 |
| 0.023 | 366 |
| 0.024 | 371 |
| 0.025 | 375 |
| 0.026 | 379 |
| 0.027 | 383 |
| 0.028 | 387 |
| 0.029 | 390 |
| 0.030 | 394 |
| 0.031 | 398 |
| 0.033 | 401 |
| 0.034 | 405 |
| 0.035 | 408 |
| 0.036 | 411 |
| 0.037 | 414 |
| 0.038 | 418 |
| 0.039 | 421 |
| 0.040 | 424 |
| 0.041 | 427 |
| 0.042 | 429 |
| 0.043 | 432 |
| 0.044 | 435 |
| 0.045 | 438 |
| 0.046 | 441 |
| 0.047 | 443 |
| 0.048 | 446 |
| 0.049 | 448 |
| 0.050 | 451 |
| 0.051 | 454 |
| 0.052 | 456 |
| 0.053 | 458 |
| 0.054 | 461 |
| 0.055 | 463 |
| 0.057 | 466 |
| 0.058 | 468 |
| 0.059 | 470 |
| 0.060 | 472 |
| 0.061 | 475 |
| 0.062 | 477 |
| 0.063 | 479 |
| 0.064 | 481 |
| 0.065 | 483 |
| 0.066 | 485 |
| 0.067 | 487 |
| 0.068 | 489 |
| 0.069 | 492 |
| 0.070 | 494 |
| 0.071 | 496 |
| 0.073 | 497 |
| 0.105 | 549 |
| 0.134 | 590 |
さいごに
非線形の構造解析していると基礎から勉強しておきたいと考えることもかと思います。
非線形の構造解析に関する本も出版されていますので、参考にしてみては如何でしょうか。
本書は応力ひずみ線図の解説から非線形解析の種類など基本的なところから解説されています。
また、接触の問題に関しては、以下の記事にて解説しているので参考にしてみてください。
もし、メッシュサイズの設定や応力特異点が発生したときの考え方など、実務的なところの基礎について知りたいと考えている方は以下の本がおすすめです。












