こんにちは、カヲルです!
高校から大学初年度くらいで扱う積分は解けるものが多いですが、一般に解析的に解けるもののほうが少ないです。
しかし、大学高学年以降や社会人になり仕事で積分を解く際は与えられた数値データから積分値を計算したい場合もあります。
このような場合に数値積分を用います。
解析的に解けるとは四則演算や微分・積分などの公式を使って式変形により解を求めることができることを言うよ。
![]()
【応用記事】微分方程式の活用 温度予測 どうやるの?①~③
台形則
高校で習った通り、1変数の積分は面積を求める計算になります。
面積の近似値を求める方法としてある関数の値を直線(1次近似)で結んで各小区間ごとに台形を作り、この台形の面積を積分区間内で全て足し合わせる方法があります。
実際の数値積分のやり方(計算式)は下記になります。
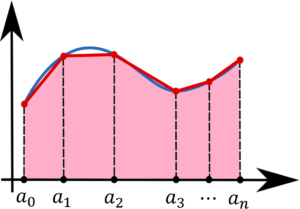

数値積分は刻み幅(台形の高さ)を小さくするほど正確な積分値となります。
コンピュータで数値積分を行う場合は精度の問題もあるので、刻み幅を異常に小さくすると繰り返し演算により計算誤差が増大する場合もあるよ。
![]()
刻み幅が等間隔の場合の台形則
上の例では刻み幅が不等間隔の場合について記載しましたが、等間隔の場合は台形則を使った積分はよりシンプルな式となります。
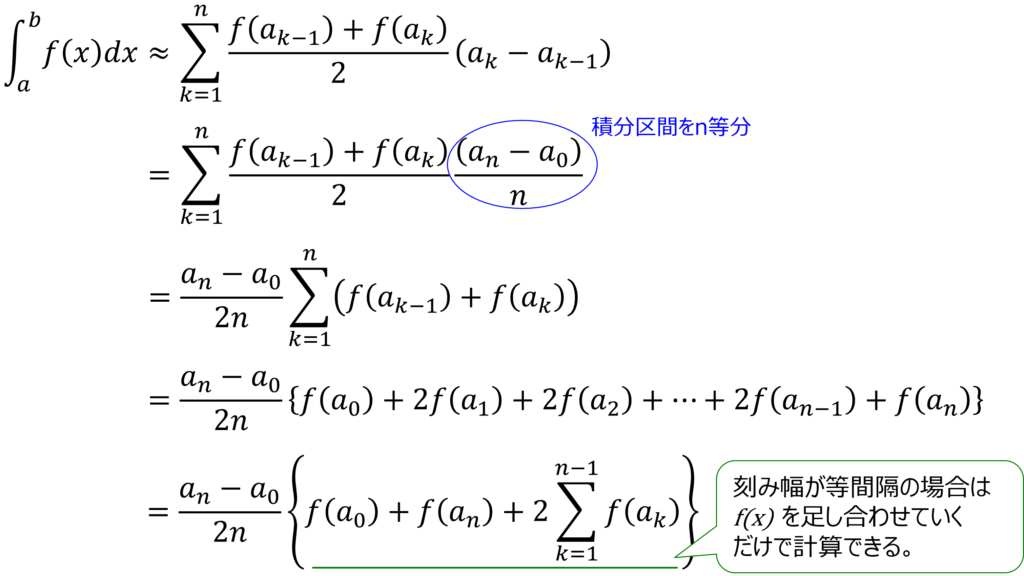
エクセルなどで表計算により数値積分する場合は刻み幅を等間隔すると手間なく解くことができるよ。
![]()
リンク
リンク



