多変数関数の微分のイメージを掴もう！

こんにちは、カヲルです！

今回は大学で習う多変数関数の微分に関して初学者に分かりやすく、イメージを掴んでもらうことを目的に書きたいと思います。

偏微分

高校で習う微分は特に意識しなかった人もいるかと思いますが、１変数関数に対しての微分でした。

この場合はxの微小変化に対するyの変化（接線の傾き）を求めるものでした。

しかし、多変数関数の微分をしたいと考えるときもあるかと思います。

１つの変数だけが微小変化した際の変化を考えるものを偏微分（partial differential）と言います。

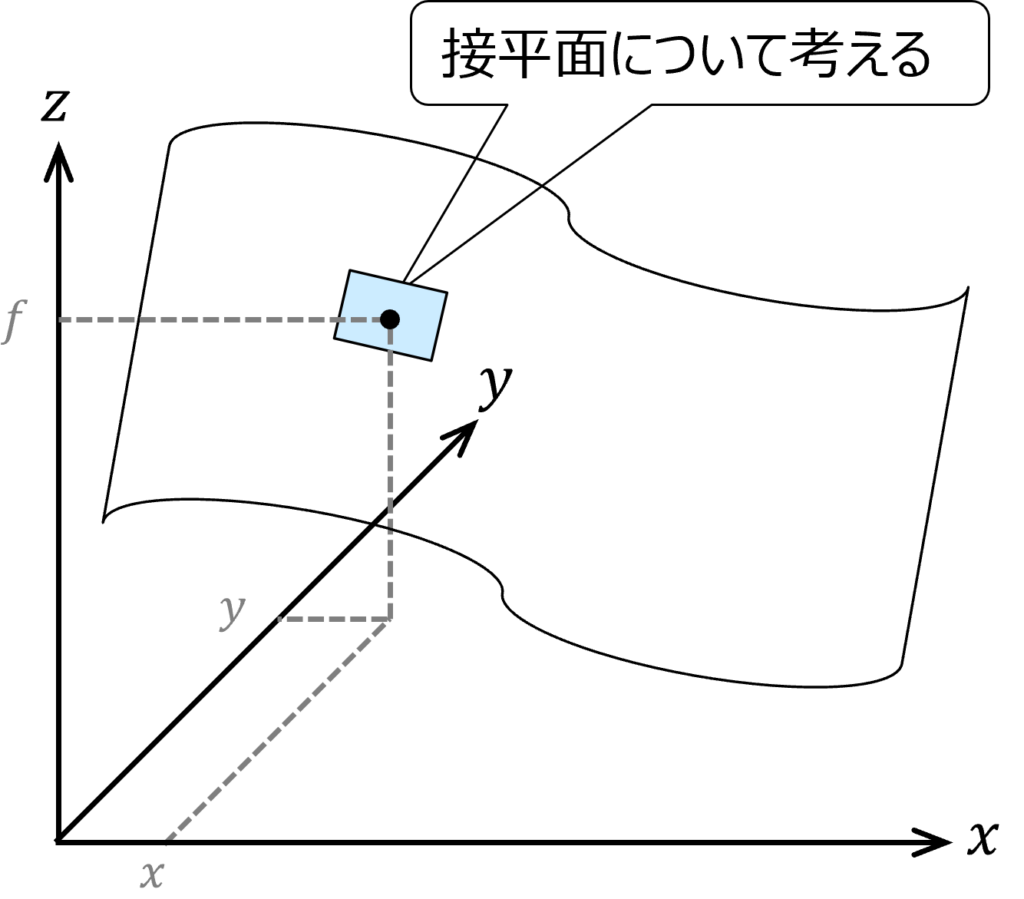
上図の様に関数fをxについて偏微分するとき、つまりx の微小変化に対するf  の変化は下式で表されます。

これはx以外を定数とみなし微分すれば計算できます。

同様にy の微小変化に対するf の変化は

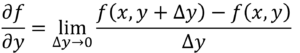
となり、y 以外を定数と見なし微分します。

全微分

偏微分は１つの変数が微小変化した際の変化のみを考えました。

しかし、複数の変数が同時に微小変化する場合もあり、その場合の微分を全微分（total differential）と言います。

全微分は偏微分が計算できれば簡単に計算できます。

f  (x, y)における全微分dfは

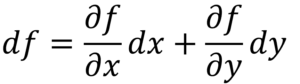
となります。