【真空ポンプの使い方】直列接続時の到達圧力の計算法

真空ポンプ（Vacuum pump）は高低温でも正常に作動するように、内部のクリアランスが設計されています。

しかし、そのクリアランスから空気がリークすることで絶対真空まで到達せず、到達圧力（最大負圧）が決められてしまいます。

使用する真空システムで、目標とする圧力まで到達しない場合、真空ポンプを直列接続することがあります。

本記事では、ポンプ２台を直列接続した場合の到達圧力の計算方法について解説します。

カヲル

真空ポンプの基本的な動作原理は下の記事を確認してね！

2022年9月24日【真空ポンプの使い方】排気時間の計算法

本記事では真空ポンプ２台を直列接続した場合の到達圧力（最大負圧）の計算方法について解説します。

Keywords｜容積移送式、真空ポンプ、バキュームポンプ、直列接続、直列運転、内部リーク、到達圧力、到達真空度、最大負圧

真空ポンプのP-Q特性

前記の通り、真空ポンプは高低温などの外乱が働いた際にも正常に作動するように、内部にクリアランスを設けられています。

通常はそのクリアランス（隙間）を通って、常にポンプ内部で空気がリークしています。（内部リークの発生）

本記事では容積移送式ポンプ（容積形ポンプ）を前提に話を進めますが、ここで簡易的なモデル化を行うこと考えてみたいと思います。

容積移送式ポンプは一定の容積を機械的に移送し続けるポンプのため、理想的には流量源と見なすことができる。
内部リークはポンプ内部の圧力差によって生じているため、オリフィスとして近似することができる。

上記仮定をもとに等価回路（空圧回路）を描くとFig. 1のようになります。

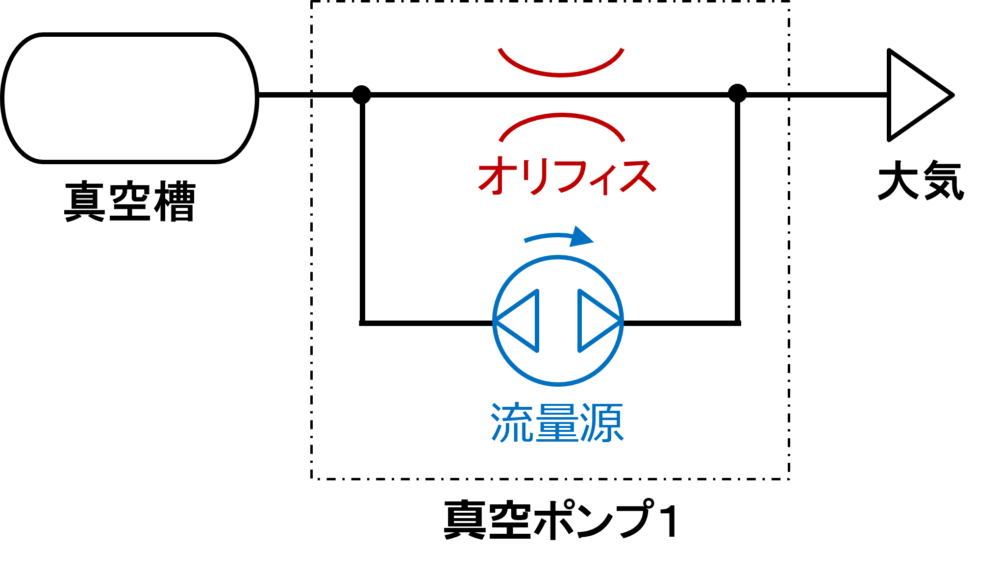
Fig. 1のモデルを前提として、横軸に真空ポンプの入口の圧力、縦軸に入口の体積流量をとったP-Q特性のグラフを描くとFig. 2のようになります。

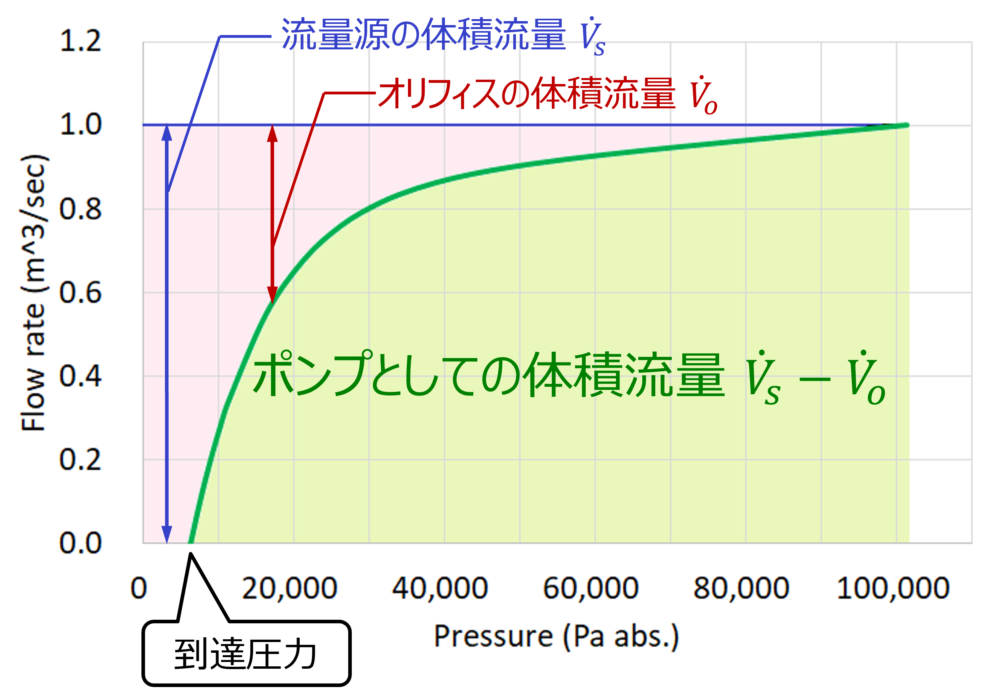
実際に真空ポンプとして流れる体積流量は、流量源の体積流量からオリフィスの体積流量（内部リーク）を引いた残りの部分、つまり、Fig. 2の緑線の流量となります。

よって、流量源の体積流量とオリフィスの体積流量が釣り合うところ（打ち消し合うところ）が真空ポンプの到達圧力となります。

同様に、ポンプ２台を直列接続した場合はFig. 3のようになります。

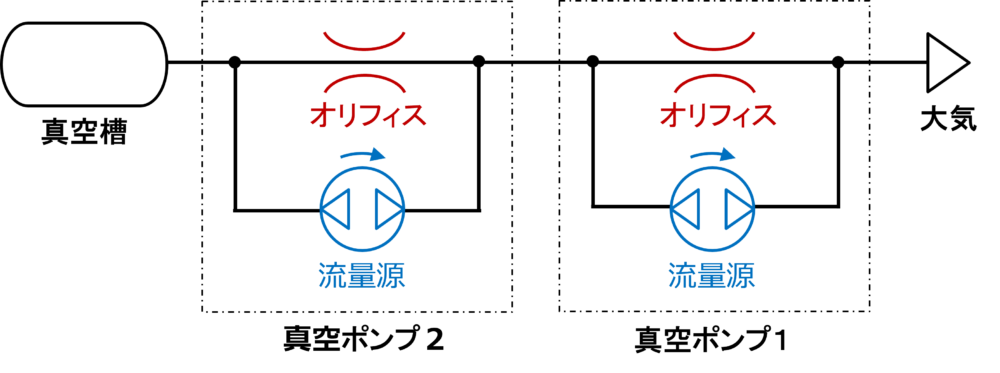
ポンプ２台を直列接続することにより、真空槽と大気の間にオリフィスが２つ入ることで到達圧力が低くなります。

リンク

２台直列接続時の到達圧力

では、実際に真空ポンプ２台を直列接続した場合の到達圧力を考えてみたいと思います。

Fig. 4で示すように大気圧を$P_0 \, (Pa \, abs.)$、1段目の真空ポンプの圧力が$P_1 \, (Pa \, abs.)$、2段目の真空ポンプの圧力が$P_2 \, (Pa \, abs.)$とします。

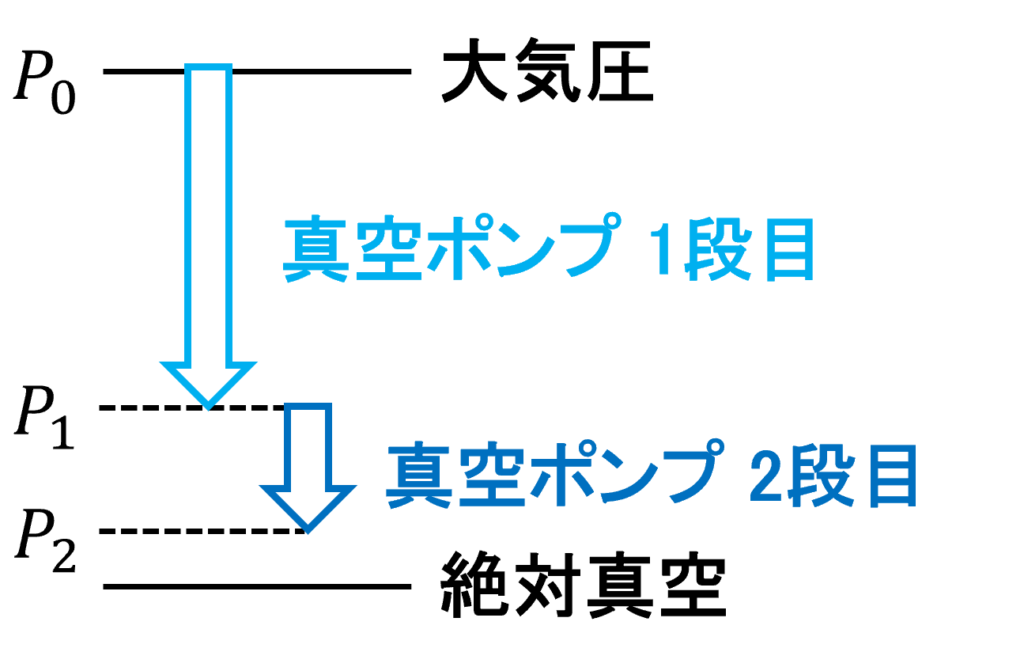
ここで補足となりますが、容積移送式ポンプにて１回転で理論的に吸い込むことのできる空気の体積（容積）を理論押しのけ容積$V_{GE} \, (m^3)$と言います。

カヲル

理論押しのけ容積の単位は、カタログ等では慣例的に$cc/rev$がよく使用されているけど、計算を行う際は$m^3$に直してね。

ポンプの回転速度を$N \, (sec^{-1})$として一定と考えた場合、真空ポンプ１と２の流量源の体積流量を$\dot{V}_{s1}, \ \dot{V}_{s2} \, (m^3/sec)$とすると、

$$\begin{eqnarray} \dot{V}_{s1} &=& V_{GE} \cdot N \tag{1}\\ \dot{V}_{s2} &=& V_{GE} \cdot N \tag{2} \end{eqnarray}$$

となります。また、オリフィスの断面積を$A \, (m^2)$、大気の密度を$\rho_0 \, (kg/m^3)$、真空ポンプ間の配管の空気密度を$\rho_1 \, (kg/m^3) $と置くと、真空ポンプ１と２のオリフィスの体積流量を$\dot{V}_{o1}, \ \dot{V}_{o2} \, (m^3/sec)$とすると、ベルヌーイの定理より、

$$\begin{eqnarray} \dot{V}_{o1} &=& A \cdot \sqrt{ \frac{2 \, (p_0 \ – \ p_1)}{\rho_0} } \tag{3}\\ \dot{V}_{o2} &=& A \cdot \sqrt{ \frac{2 \, (p_1 \ – \ p_2)}{\rho_1} } \tag{4} \end{eqnarray}$$

となります。到達圧力時は流量源とオリフィスの体積流量が釣り合うので、

$$\begin{eqnarray} \dot{V}_{s1} &=& \dot{V}_{o1} \tag{5} \\ \dot{V}_{s2} &=& \dot{V}_{o2} \tag{6} \end{eqnarray}$$

となります。空気の気体定数を$R \, (J/(kg \cdot K)$、温度を$T \, (K)$と置くと、理想気体の状態方程式と密度の定義より、

$$\begin{eqnarray} \rho_0 = \frac{p_0}{R \cdot T} \tag{7} \\ \rho_1 = \frac{p_1}{R \cdot T} \tag{8} \end{eqnarray}$$

となります。式（１）から（８）までの連立方程式より$p_2$を求めます。

式（５）に式（１）、（３）を代入、式（６）に式（２）、（４）を代入すると、

$$\begin{eqnarray} V_{GE} \cdot N &=& A \cdot \sqrt{ \frac{2 \, (p_0 \ – \ p_1)}{\rho_0} } \tag{9}\\ V_{GE} \cdot N &=& A \cdot \sqrt{ \frac{2 \, (p_1 \ – \ p_2)}{\rho_1} } \tag{10} \end{eqnarray}$$

となり、式（９）に式（１０）を代入しすると、

$$\begin{eqnarray} A \cdot \sqrt{ \frac{2 \, (p_0 \ – \ p_1)}{\rho_0} } &=& A \cdot \sqrt{ \frac{2 \, (p_1 \ – \ p_2)}{\rho_1} }\tag{11} \\ \\ \frac{p_0 \ – \ p_1}{\rho_0} &=& \frac{p_1 \ – \ p_2}{\rho_1} \tag{12} \end{eqnarray}$$

となり、式（１２）に式（７）、（８）を代入すると、

$$\begin{eqnarray} \frac{RT \, (p_0 \ – \ p_1)}{p_0} &=& \frac{RT \, (p_1 \ – \ p_2)}{p_1} \tag{13} \\ \\ 1 \, – \, \frac{p_1}{p_0} &=& 1 \, – \, \frac{p_2}{p_1} \tag{14} \end{eqnarray}$$

となり、式（１４）を$p_2$について解くと下式のようになります。

$$ p_2 = \frac{{p_1}^2}{p_0} \tag{15}$$