【真空ポンプの使い方】排気時間の計算法

真空ポンプ（Vacuum pump）は半導体、電子部品、自動車、医療、食品など多岐にわたる産業分野で活用されています。

本記事は真空ポンプに真空槽（真空チャンバー）が接続されている場合に、真空槽内の圧力が所定の圧力まで下がるのにかかる所要時間（排気時間）を計算する方法を解説します。

カヲル

真空ポンプは身近なところで活用されているよ。

気になる人は日本真空工業会のHPも見てみてね！

https://jvia.gr.jp/vacuum/museum.html

本記事では真空槽（真空チャンバー）が接続された真空ポンプの排気時間の計算方法について解説します。

Keywords｜容積移送式、運動量輸送式、真空ポンプ、バキュームポンプ、真空槽、真空タンク、排気時間、到達時間、排気速度、排気曲線、微分方程式

真空ポンプの種類

真空槽の中の気体を排気して、真空を作り出すための装置として真空ポンプが使われます。

真空ポンプには多くの種類があり、動作原理や作動圧力範囲はそれぞれ異なります。

動作原理としては大きく分けて、容積移送式ポンプと運動用輸送式ポンプがあります。

容積移送式ポンプ

容積移送式ポンプ（容積形ポンプ）とは、一定の容積を機械的に隔離して移送するポンプを言います。

ここで具体的なイメージを持つために、ビーカーの中の水を注射器で移動させる場合を考えてみましょう。

まず、注射器の先端を水の中に入れ、ピストンを引っ張ると水が吸入されます。

つぎに、注射器を移動し、ピストンを押すとビーカーの外に水が排出されます。

これは単純に注射器を使って水を移動させただけですが、機械的な視点で見ると注射器内の容積分だけビーカーから容積が切り離され、その後、容積が移送（移動）されたことになります。

このメカニズムを用いたものが容積移送式ポンプと呼ばれるものです。

実際のポンプでは逆止弁を設けるなどしてポンプの入口と出口を二系統に分け、ピストンの往復操作だけで水や空気などの流体を移動させることができるようにしています。

運動量輸送式ポンプ

運動量輸送式ポンプとは、気体又は液体の分子に方向性のある運動（運動量）を与え、ポンプの入口から出口へ向かって連続的に流体を輸送するポンプを言います。

身近な例では扇風機や洗濯機などがあります。

本記事では容積移送式ポンプのほうを扱い、運動量輸送式ポンプは扱いません。

リンク

真空ポンプの排気曲線

では、真空ポンプの排気曲線を計算する式を求めてみましょう。

排気曲線とは

真空槽に真空ポンプを接続し、ポンプを動作させると時間の経過とともに真空槽内の気体の圧力が低下していきます。このときの圧力と時間の関係をグラフ化したものを排気曲線と言います。

まず、外部リークのない完全に密閉された真空槽に真空ポンプが接続され、合計容積$V \, (m^3)$の中に圧力$p_1 \, (Pa \ abs.)$の気体が満たされていることを考えます。

この状態から、Fig. 1のようにポンプの作用により、体積$\Delta V \, (m^3)$だけ気体が取り出されます。

内部の気体を排出した後の真空ポンプが真空槽と再び接続され、真空槽に残った$V \, – \, \Delta V $の気体が合計体積$V$の中に広がり、圧力が低下します。

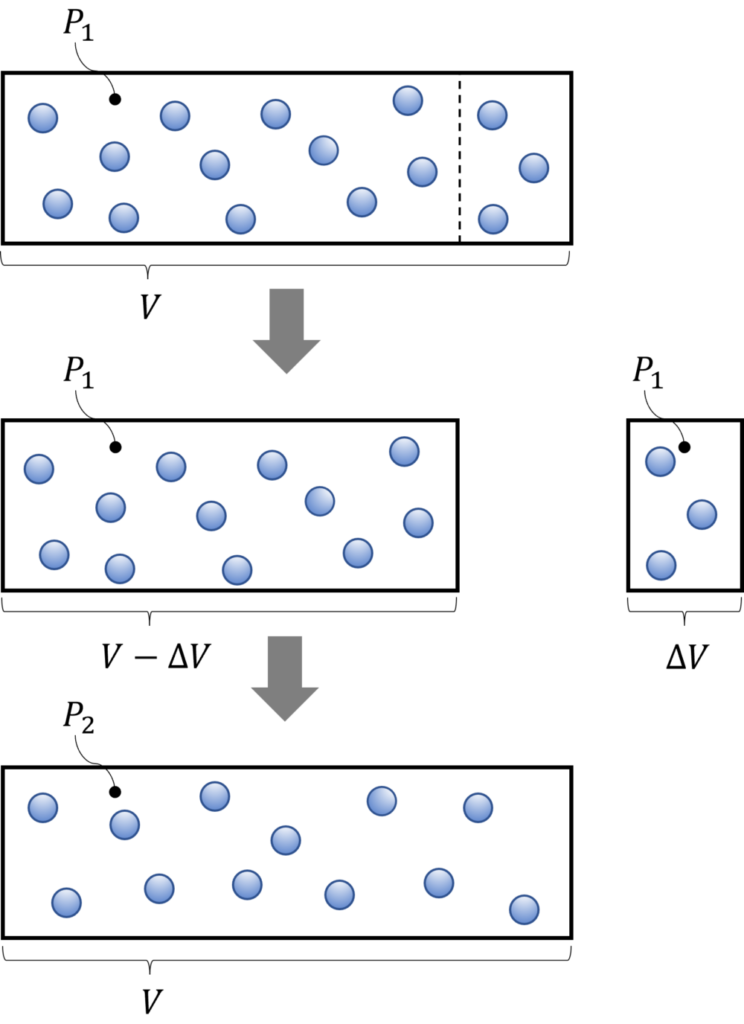
このとき、気体の温度が一定（等温変化）だと仮定すれば、圧力$p_2 \, (Pa \ abs.)$はボイルの法則より、

$$\begin{eqnarray} p_1 \, (V – \Delta V) &=& p_2 \, V \tag{1} \\ p_2 &=& p_1 \, \frac{V – \Delta V}{V} \tag{2} \end{eqnarray}$$

となり、圧力変化$\Delta p$は、

$$\begin{eqnarray} \Delta p &=& p_2 \, – \, p_1 \tag{3} \\ &=& p_1 \, \frac{V – \Delta V}{V} \, – \, p_1 \, \frac{V}{V} \tag{4} \\ &=& \, – \, p_1 \, \frac{\Delta V}{V} \tag{5} \\ \end{eqnarray}$$

となります。ポンプ動作は繰り返し行われますが、$p_1$はその時々の圧力であるため、$p$と置き換えと、

$$\Delta p = \, – \, p \, \frac{\Delta V}{V} \tag{6}$$

となり、ポンプ動作の繰り返しの周期を$\Delta t \, (sec)$とし、両辺を$\Delta t$で割ると、

$$ \frac{\Delta p}{\Delta t} = \, – \, \frac{p}{V} \, \frac{\Delta V}{\Delta t} \tag{7} $$

となります。ここで$\Delta V \, / \, \Delta t$は排気速度（体積流量）を示しているので、$S_e$と置き換え、さらにポンプ動作は連続的に行われていると仮定し、極限をとると、

$$ \frac{dp}{dt} = \, – \, \frac{p}{V} \, S_e \tag{8} $$

となり、変数分離すると、

$$ \frac{1}{p} \, dp = \, – \, \frac{S_e}{V} \, dt \tag{9} $$

となります。両辺を積分すると、$C_1$を任意定数（積分定数）として、

$$\begin{eqnarray} \int \frac{1}{p} \, dp &=& \, – \, \frac{S_e}{V} \, \int dt \tag{10} \\ \ln p &=& \, – \, \frac{S_e}{V} \, t \, + \, C_1 \tag{11} \end{eqnarray}$$

となります。（$\ln$は底を$e$とする自然対数です。）

両辺に指数をとると、

$$\begin{eqnarray} e^{\ln p} &=& e^{- \, \frac{S_e}{V} \, t \, + \, C_1} \tag{12} \\ p &=& e^{- \, \frac{S_e}{V} \, t} \cdot e^{C_1} \tag{13} \end{eqnarray}$$

$e^{C_1}$を任意定数$C_2$と置き替えると、

$$p = C_2 \cdot e^{- \, \frac{S_e}{V} \, t} \tag{14}$$

となります。初期$(t = 0)$の真空槽の圧力を$p_0$とすると、下式のようになります。

$$p = p_0 \cdot e^{- \, \frac{S_e}{V} \, t} \tag{15}$$

例題として、$p_0 = 101,325 \, Pa \, abs.$、$S_e = 2 \times 10^{-3} \, m^3/sec$、$V = 0.01 \, m^3$のときのグラフを描いてみます。

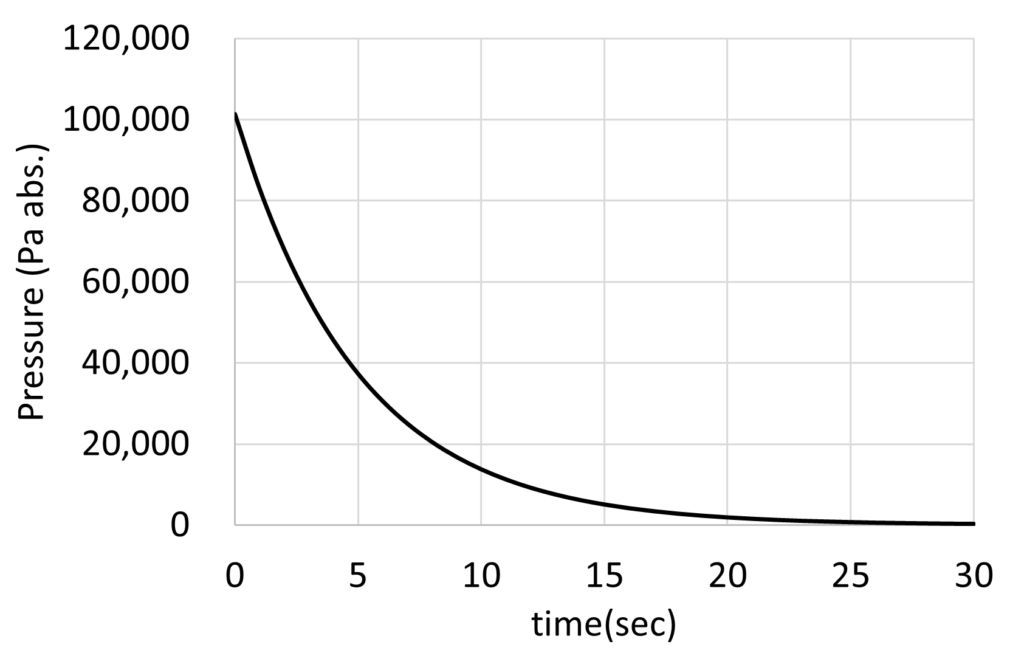
Fig. 2が排気曲線と呼ばれるものになります。さらに、このグラフの縦軸を対数にするとFig. 3にようになります。

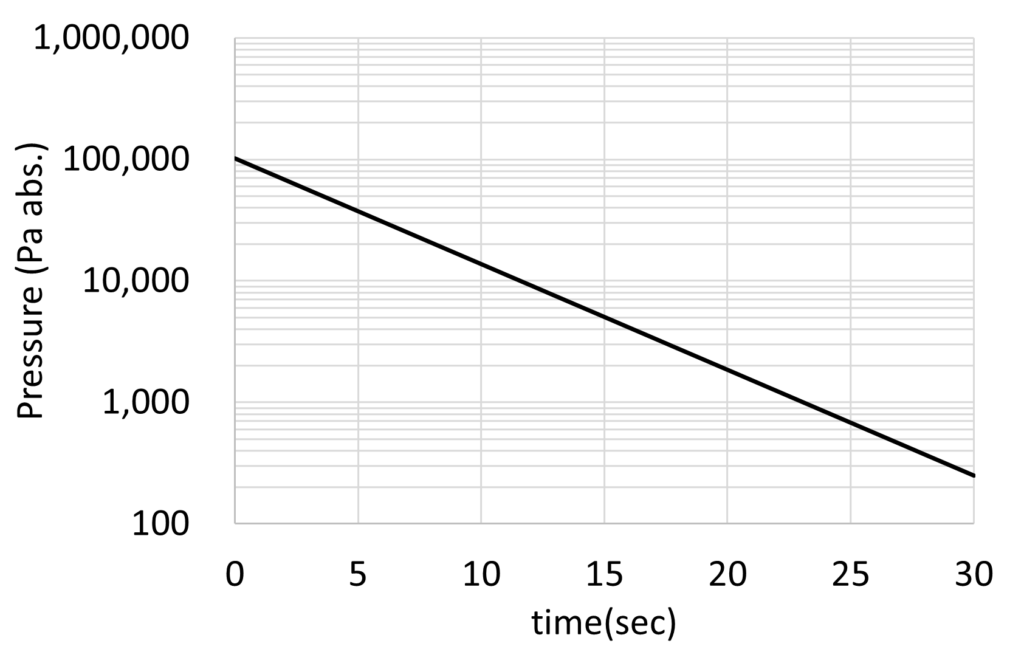
Fig.3の直線の傾きは「圧力低下の速さ」を表します。そして、その逆数の$V/S_e$は「圧力低下の遅さ」を表し、真空システムの排気の時定数$\tau \, (sec)$と呼ばれます。

カヲル

理想の真空ポンプ（上記）は0 Pa abs.まで到達するはずだけど、実際の真空ポンプではポンプ内部に隙間があり、リークが発生するので0 Pa abs.まで到達しないから注意してね。

リンク

真空ポンプの排気時間

式（１５）を式変形し、圧力$p_0$から圧力$p_1$まで下がるのにかかる時間$t$は、

$$\begin{eqnarray} \frac{p_1}{p_0} &=& e^{- \, \frac{S_e}{V} \, t} \tag{16} \\ \ln \left( \frac{p_1}{p_0} \right) &=& \ln e^{- \, \frac{S_e}{V} \, t} \tag{17} \\ t &=& – \, \frac{V}{S_e} \, \ln \left( \frac{p_1}{p_0} \right) \tag{18} \\ t &=& \frac{V}{S_e} \, \ln \left( \frac{p_0}{p_1} \right) \tag{19} \\ \end{eqnarray}$$

となります。自然対数から底を10とする常用対数を使った式に変換すると、下式のようになります。

$$t = 2.303 \times \frac{V}{S_e} \, \log_{10} \left( \frac{p_0}{p_1} \right) \tag{20} $$

常用対数に変換した式を載せていますが、コンピュータで計算する場合は式（１９）にて計算しましょう。

カヲル

この計算は、配管の長さや太さ、配管抵抗や漏れなどを考慮してないので、実際には安全率を見込んで設定してね。

関連記事（内部リークの考え方）