モータの解析手法として、電気等価回路法、有限要素法、磁気回路法(パーミアンス法)があります。これらの特徴はそれぞれ以下のようになります。
- 電気等価回路法
モータを抵抗、インダクタンスと起電力でモデル化し、定常状態から過渡状態まで少ない計算負荷で求めることができ、駆動回路や制御系と組み合わせた解析が容易。
しかし、等価回路定数はあらかじめ実験などで求める必要がある。 - 有限要素法
モータを要素分割し、各要素で電磁界方程式を近似計算するもので、代表的なツールにJSOL社のJMAGなどがある。
形状や寸法を考慮した詳細な解析が可能な一方で計算負荷が非常に大きく、駆動回路や制御系と組み合わせた動解析は難しい。 - 磁気回路法(パーミアンス法)
磁気回路における起磁力と磁束を電気回路における電圧と電流の関係と同様に扱うことで、モータ内部の磁気現象を解析する手法。
計算負荷も比較的軽く、メカニズム(からくり)を理解しながら設計を行うことができるため、近年注目されているモデルベース開発(MBD:Model Based Development)とも相性がよい。
本記事ではモータ解析の第一歩として、まずは簡単な磁気回路の計算方法について解説するね!
磁気回路の要素と法則
透磁率\(\mu\)が小さい場合は磁束分布を考えることになりますが、透磁率\(\mu\)が大きい材料では磁束は材料の中を通り外部に漏れにくくなります。
このことから、磁束の通り道を電流の通り道と同様に考えたほうが扱いやすく、この磁束の通り道を磁気回路または磁路(Magnetic circuit)と呼びます。
起磁力
磁気回路\(c\)に沿って一周する磁界\(\boldsymbol{H}\)を線積分すると
\(F_m=\oint_c \boldsymbol{H} \cdot d \boldsymbol{l}=\oint_c H dl=Ni \quad [AT]\)
となります。ここで\(N\)はコイルの巻数、\(i\)は電流になります。(アンペアの周回積分の法則)
上記を電気回路における起電力(Electromotive force)に対応させて、起磁力(Magnetomotive force)といい、\(F_m\)で表します。

磁束
磁気回路の断面積を\(S\)、磁束密度を\(\boldsymbol{B}\)とおくと、この断面を通る磁束\(\phi\)は
\(\phi=\oint_s \boldsymbol{B} \cdot d \boldsymbol{S}=\oint_s B_n dS \quad [Wb]\)
となります。これは電気回路において導体の断面積\(S\)を流れる電流\(i\)に対応します。
磁気抵抗
電気回路において電気抵抗\(R\)は、\(R = \frac{v}{i}\)で定義されます。(オームの法則)
磁気回路ではこれに対応させて
\(\displaystyle R_m = \frac{F_m}{\phi} \quad [\frac{1}{H}]\)
となる量を定義し、これを磁気抵抗(リラクタンス, Reluctance)といい、\(R_m\)で表します。
ここで、任意の2点間の長さを\(l\)とし、透磁率\(\mu\)と断面積\(S\)がいたるところで一定であるとすると磁気抵抗\(R_m\)は
\(\displaystyle R_m= \frac{l}{\mu S}\quad [\frac{1}{H}]\)
となります。
また、磁気抵抗の逆数はパーミアンス(Permeance)といい、\(P\)で表します。
電気回路と磁気回路のアナロジー(対照表)
上記で示した起磁力、磁束と磁気抵抗の関係を整理し、電気回路と比較すると下表のアナロジーがあります。
| 電気回路 | 磁気回路 |
|---|---|
| 電圧 \(v \quad [V]\) | 起磁力 \(F_m = Ni \quad [A]\) |
| 電流 \(i \quad [A]\) | 磁束 \(\phi \quad [Wb]\) |
| 導体断面積 \(S \quad [m^2]\) | 磁路断面積 \(S \quad [m^2]\) |
| 導体長 \(l \quad [m]\) | 磁路長 \(l \quad [m]\) |
| 導電率 \(\rho \quad [S/m]\) | 透磁率 \(\mu \quad [H/m]\) |
| 電気抵抗 \(\displaystyle R = \frac{l}{\rho S} \quad [\Omega]\) | 磁気抵抗 \(\displaystyle R_m = \frac{l}{\mu S} \quad [\frac{1}{H}]\) |
| コンダクタンス \(\displaystyle G = \frac{\rho S}{l} \quad [S]\) | パーミアンス \(\displaystyle P = \frac{\mu S}{l} \quad [H]\) |
磁気回路の法則(キルヒホッフの法則)
上記の対照表で示す通り、電気回路と磁気回路にはアナロジーがあることから、電気回路におけるキルヒホッフの法則を適用して磁気回路の計算を行うことができます。
節点方程式 \( \displaystyle \sum_{i}\phi_i = 0 \)
閉路方程式 \( \displaystyle \sum_{i}{F_{m \, i}} = \sum_{j}{R_j \, \phi_j} \)
これらの性質を用いると、複雑な磁気回路も容易に計算することができます。
磁気回路の計算
ここで、いくつかのパターンの磁気回路の計算例を示します。
最も基本的な磁気回路(トロイダルコア)
Fig. 1に示すトロイダルコアにて、外径を\(D \, [m]\)、内径を\(d \, [m]\)とおくと磁路長\(l \, [m]\)は
となります。よって、断面積を\(S \, [m^2]\)とおくと磁気抵抗\(R_m \, [1/H]\)は
となり、磁束\(\phi \, [Wb]\)は
となります。

磁気抵抗の直列接続(空隙付きトロイダルコア)
Fig. 2に示す空隙付きトロイダルコアにて、磁性体部分の磁路長を\(l_1 \, [m]\)、透磁率を\(\mu \, [H/m]\)、空隙長を\(l_2 \, [m]\)、空隙部分の透磁率を\(\mu_0 \, [H/m]\)とし、断面積はいづれも\(S \, [m^2]\)として、空隙部分も磁束は一様で外に広がっていないものとします。
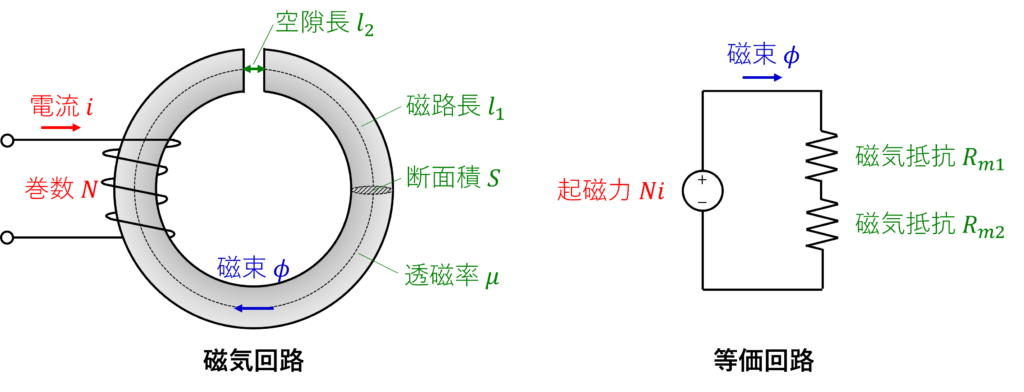
磁性体部分の磁気抵抗\(R_{m1} \, [1/H]\)と空隙部分の磁気抵抗\(R_{m2} \, [1/H]\)は直列接続の関係にあるため、電気回路と同様に合成磁気抵抗\(R_m \, [1/H]\)は
となります。ここで、\(l_1\)と\(l_2\)で数値のオーダーに大きな違いがなければ、\(\mu \gg \mu_0\)となる材料の組み合わせであれば以下に近似できます。
実際の製品設計では、\(l_1\)と\(l_2\)はどちらもmmオーダーであることが多いので、式(2-3)を適用できることが多いよ!

実際に数字を代入して計算してみると分かりやすいですね。
この空隙の計算は、モータのエアギャップ(ロータ~ステータ間の空隙)の計算で必要になるので、しっかり理解しておこう!
磁気抵抗の並列接続
次にFig. 3のような三脚鉄心について考えます。
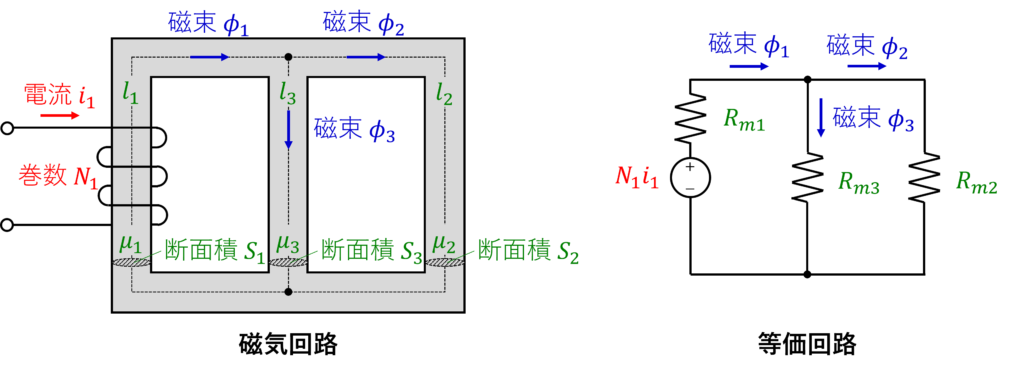
各脚の磁気抵抗\(R_{m1}\)、\(R_{m2}\)、\(R_{m3} \, [1/H]\)は
となります。ここで、回路方程式を立てると
となり、連立方程式を解いて各々の磁束\(\phi_1\)、\(\phi_2\)、\(\phi_3 \, [Wb]\)を求めると
となります。
複数の起磁力がある磁気回路
Fig.4のような三脚鉄心に複数の巻線が巻かれた場合を考えます。

Fig. 3の三脚鉄心と同様に回路方程式を立てると
となり、連立方程式を解いて各々の磁束\(\phi_1\)、\(\phi_2\)、\(\phi_3 \, [Wb]\)を求めると
となります。
この三脚鉄心の計算を応用すると、モータの磁気回路(ロータやステータ)の計算ができるようになるよ!
まとめ
本記事では、モータの解析に使用される磁気回路法(パーミアンス法)の基礎について解説しました。
磁気回路法にてモータを解析するにあたり、やはり電磁気学の知識は必要になってきます。
電磁気学を学習する際には、基礎的なことがしっかり書かれていて、且つ実際の製品設計にも応用できるように書かれているものがおすすめです。
参考として、製品設計の実務へも応用できる書籍を紹介します。


