こんにちは、カヲルです!
品質管理の分野においてある製品や部品の工程の能力を定量的に評価する指標として工程能力指数(process capability index)というものがあります。
今回は公差の基礎、統計学の基礎を学び、最後に工程能力を求める方法について書きたいと思います。
公差の基礎知識
工程能力の話に入る前にまずは公差(tolerance)とは何かついて説明したいと思います。
部品の互換性
中世より前の世界では農具などの生活物資をそれぞれの職人が一人で製品の形まで完成させていました。各部品の組み立てはひとつひとつ手作業ですり合わせを行い、職人の技能や経験に頼って製造されていました。
やがて中世末期(15世紀ごろ)になると商人や地主などが工場を建ててそこに大量の労働者を集めて各製造工程を分担させ、効率的に生産を行うようになりました。この製造形態のことを工場制手工業(manufacture)と言いますが、このころもまだ職人の技能や経験に頼って組み立てが行われていました。
そして18世紀半ばに産業革命(industrial revolution)がおこると以前には考えられないほど大量に製造ができるようになりました。しかし、これまでの様に職人による組み立てを行うとその部分がネック工程となり、生産効率が著しく落ちてしまいます。
そこでこの課題を解決する手段として他の部品との組み立て部の寸法をある幅で管理しようという発想が生まれました。この概念を他者に分かるように明確に示したものが公差となります。
これにより部品の互換性が確保され、生産効率が向上しました。
品質とコスト
製品の組み立て以外にも設計者が期待した通りの機能(Function)を製品が発揮するためには各寸法に公差を入れて管理する必要があります。
しかし、材料のばらつき、気温や湿度の作業環境の変化、加工工具の摩耗、作業者の身体面、精神面のコンディションなどから製造上必ずばらつきが出ます。
管理する公差の幅を狭くすれば組み立て時の互換性や性能の機能が安定し、品質が良くなりますが製造コスト(Manufacturing cost)が上昇してしまいます。逆に公差の幅を広くするとその製品を破棄したり手直ししたりする必要が出てくるため損失が発生します。このコストのことを損失コスト(Loss cost)と言います。
損失コストと製造コストとの関係は下図のようなイメージとなります。

なお、公差の幅を狭くすることを「公差を厳しくする」、「公差をきつくする」や「公差を詰める」などと言い、逆に広くすることを「公差を緩める」、「公差を緩和する」や「公差をあまくする」などと言います。
公差はどのように決めるのか
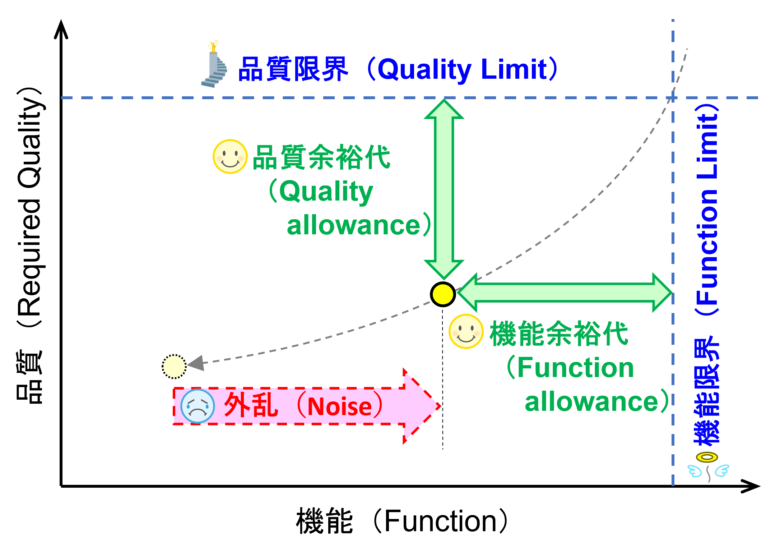
製品を設計するにあたり、例えば作動音は〇〇 dB(A)以下にしたいなど商品性の目標値を決めます。ここではその目標値を品質限界(Quality Limit)と定義します。
その品質限界を達成するために制御因子、公差、使用環境や制御不能なノイズ(誤差因子)などを抽出し、機能限界(Function Limit)を超えないロバストな設計をしていきます。機能限界は上記の例で言えば残留アンバランスなどが該当します。
このプロセスでは機能展開やメカニズムを解明し、CAE(Computer Aided Engineering)や実験などを繰り返しながら、最終的に図面に落としていきます。
ここで、図面の公差上下限でも機能限界を超えないように設計する必要があり、公差解析(Tolerance analysis)を実施して確認し公差を設定していきます。
統計学の基礎知識
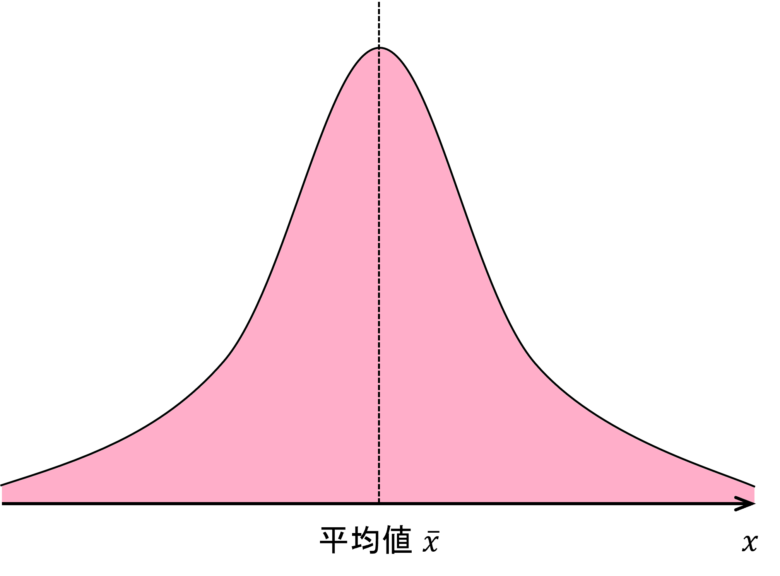
一般に寸法や特性値などは正規分布(Gaussian distribution)に従うことが多いことが知られています。正規分布とは下図の様に平均値(Mean value, Average value)に集中するような分布を言います。
工程能力指数を求める際には正規分布に従っていることが前提条件となります。
平均値(Mean value, Average value)を理解しよう
平均は算術平均(相加平均)、幾何平均(相乗平均)、調和平均や対数平均などがありますが、ここでは算術平均のことを言います。
n個のデータの値がx1, x2, x3, …, xnであるとすると算術平均![]() の定義は下式となります。
の定義は下式となります。
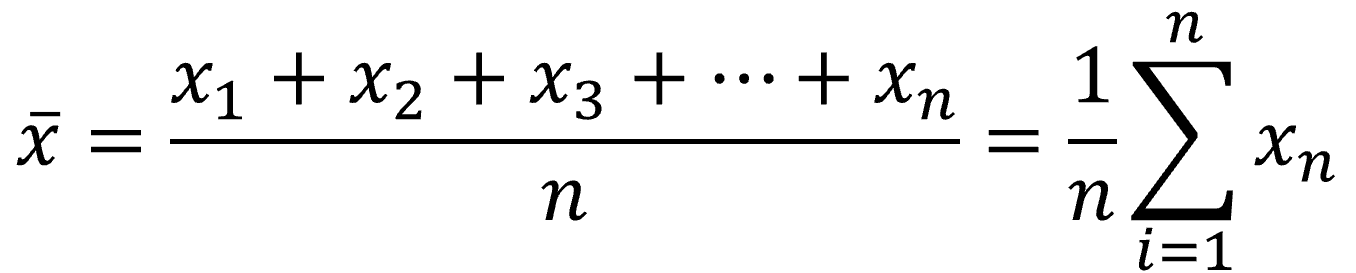
なお、![]() はエックスバーと読みます。
はエックスバーと読みます。
分散(Variance)を理解しよう
データ分析を行うあたり、データがどれだけ散らばっているか(=ばらつき)を示す指標として分散![]() というものがあります。
というものがあります。
分散が大きくなると前記グラフの正規分布の山の幅が広くなり、逆に分散が小さくなると正規分布の山が鋭くなります。また、全ての値が同じ場合はゼロとなります。
分散の定義は下式となります。
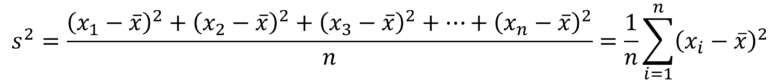
ここでデータに対する基準値(ここでは平均値)との差のことを偏差(Deviation)と言い、上式の![]() の部分が該当します。
の部分が該当します。
この偏差を合計したものがばらつきを示す指標となりそうですが、偏差はプラスとマイナスと値をとるため、単純に合計すると打ち消しあい、ばらつきがゼロになってしまいます。そこで全てを正の値とするため、数学(解析学)上の扱いが容易な二乗をとって偏差を合計します。
この合計値はデータの個数が増えると値が増えるため、データが多いほうがばらつきが大となってしまいます。そこでデータの個数nで割り、平均をとることでスケーリングします。これが分散となります。
標準偏差(Standard deviation)を理解しよう
前記で分散について説明しましたが二乗を用いることで数字が大きくなり、単位も元のデータの二乗となるため、使い勝手悪くあまり用いられません。
やはり、データのばらつきを示す指標としては元データと同じスケールにしたいと思うと思います。そこで偏差![]() の平方根(ルート)をとったものが標準偏差σとなります。
の平方根(ルート)をとったものが標準偏差σとなります。
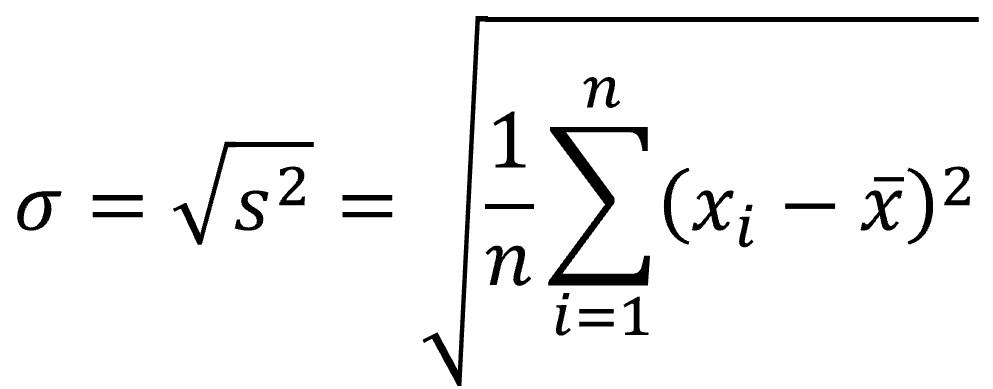
実際に工程能力指数をExcelを使って求めよう!
工程能力指標を求める際には、先ず平均値と標準偏差を求めます。
もし、社内規定などでデータの個数が30以上や100以上と定めれている場合はそれに合わせて測定を実施します。
水増し係数を求めよう
前項までの平均や標準偏差の式は前提条件があり、それは母集団(Population)全体のデータが分かっている場合に適用されることです。
実際には全数を測定することは難しく、標本(Sample)から標準偏差を計算する必要がありますが、標本から計算した標準偏差は母集団から計算した標準偏差より小さくなります。
そこでその補正をするための係数を水増し係数(Bias correction factor)と言い、データの個数nの場合は下式で求めます。
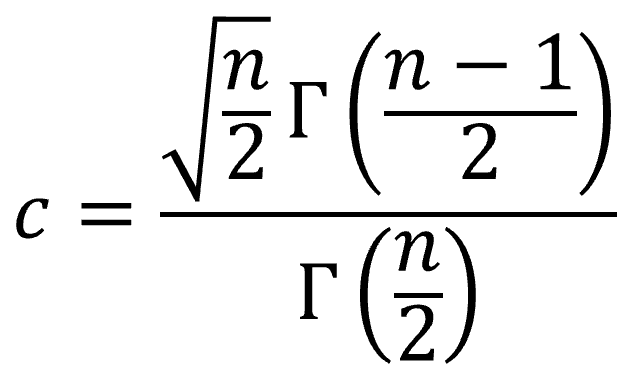
巻末にサンプルとしてExcelファイルを付けますが、平方根はExcelのSQRT関数を使うと求めることが出来ます。
また、Γ(n)はガンマ関数と言い、階乗の概念を複素数全体に拡張した関数となります。階乗との関係は「n! = Γ(n + 1)」となります。
ガンマ関数はExcelのGAMMA関数で求めることが出来ます。
標準偏差を求めよう
標準偏差はExcelのSTDEV.P関数を使うと求めることができます。
母集団の標準偏差(推定値)はSTDEV.P関数で求めた標準偏差に水増し係数を掛けたものとなります。
工程能力指数を求めよう
工程能力指数には図面の公差幅に対してばらつき幅を評価するCpと図面公差の中心値とデータの平均値との偏りを考慮して評価するCpkの2種類があります。
公差上限をUSL(Upper Specification Limit)、公差下限をLSL(Lower Specification Limit)、水増し係数をc、標準偏差をσとおくとCpとCpkは下式より求めることが出来ます。
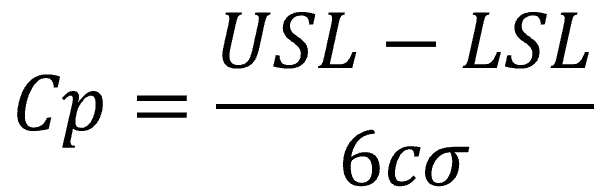
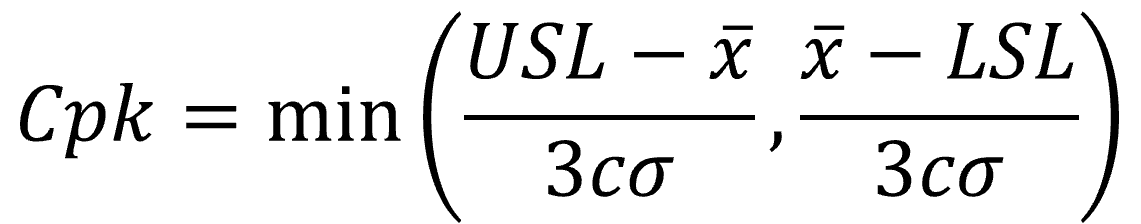
Cpkは2つの計算結果のどちらか小さいほうを採用するためExcelのMIN関数を使用して求めます。
まとめ
工程能力指数の計算は統計学を基にしていますが、数学の中で確率・統計は人気がある科目ではなく、最初はとっつきにくい方も多いかと思います。
算出にあたりバックグランドは数学や品質工学に譲りますが、先ずは手持ちデータからCpやCpkを計算し慣れてみては如何でしょうか。
工程能力指数の計算サンプルはこちらよりダウンロードできます。



