超・基礎から解説！ナビエ・ストークス方程式の導出【流体力学】

物理現象を記述した方程式を支配方程式（または基礎方程式）と言います。

流体力学（Fluid mechanics）分野での支配方程式は連続の式、ナビエ・ストークス方程式、エネルギー方程式があります。

これらは質量保存則、運動量保存則、エネルギー保存則を式で表したものになります。

空気などの流体の流れをコンピュータ上で計算する際にはSTAR-CCM+などの流体解析ソフト（3D CAE）を使うことが多いですが、計算結果の妥当性を検証する際や計算結果のレビュー（DR）をする際に、基礎知識としてこれらの方程式を理解しておく必要があります。

また、MATLABなどを用いてイチから1Dモデルを作成する際にもこれらは理解しておく必要があります。

本記事では、運動量保存則（ニュートンの運動の第二法則）を記述する式であるナビエ・ストークス方程式について解説します。

ナビエ・ストークス方程式とは

ニュートンの運動方程式

高校から大学にかけてニュートン力学を習いますが、普段生活する上での身の回りの現象は全てこのニュートン力学で説明することができます。

質量を$m \, (kg)$、位置を$\boldsymbol{r} \, (m)$、時間を$t \, (s)$、力を$\boldsymbol{F} \, (N)$と置くと、ニュートンの運動方程式は以下のように書くことができます。

$$ m \frac{d^2\boldsymbol{r}}{dt^2} = \boldsymbol{F} \tag{1}\\ $$

ニュートン

物理の方程式は原因を右辺、結果を左辺に書くのが慣例になっているよ！

運動方程式は物体に働く力$\boldsymbol{F}$が分かれば、物体の運動（位置$\boldsymbol{r}$）が完璧に分かる方程式だよ。

心太

高校まではベクトルを$\vec{F}$というように矢印をつけて表しますが、大学では$\boldsymbol{F}$というように太字で表しますね。

なお、ニュートンの運動方程式は質点（しつてん）の運動を求める式になっています。

カヲル

質点とは物体の重心にその全質量が集まっていると見なし、その点の位置・運動によって物体の位置・運動を代表させる力学的概念のことだよ。

ナビエ・ストークス方程式の解説

ニュートンの運動方程式は質点の運動を取り扱っていましたが、ナビエ・ストークス方程式（Navier-Stokes equations）は流体の運動を取り扱う流体力学における支配方程式です。

ナビエ・ストークス方程式はニュートンの運動方程式をベースに流体用にカスタマイズした式となっています。

流体力学で取り扱う力は主に以下の３つがあります。

圧力による力 $\boldsymbol{F_p}$
粘性力（流体のネバネバさからくる抵抗力） $\boldsymbol{F_v}$
重力などの外力 $\boldsymbol{F_g}$

流体力学ではこれらの合力から流体の運動を考えます。

カヲル

ニュートンの運動方程式と同様にナビエ・ストークス方程式でも力は右辺に書くよ。

次に右辺で示される流体の運動について考えてみよう！

ボールなどの質点の運動を考える場合は速度を$\boldsymbol{v}$と置くと加速度は$\frac{d}{dt}\boldsymbol{v} \, \left( =\frac{d^2}{dt^2}\boldsymbol{r} \right) $で表されました。

空気や水などの流体の流れる速度を流速と言いますが、流速を$\boldsymbol{v}$と置くと$\frac{D}{Dt}\boldsymbol{v}$と表されます。（$\frac{D}{Dt}$は物質微分と呼ばれますが、こちらに関してはのちの項で詳しく解説します。）

以上より、流体の運動方程式は以下の形で表されます。

$$ m \frac{D\boldsymbol{v}}{Dt} = \boldsymbol{F_p} + \boldsymbol{F_v} + \boldsymbol{F_g} \tag{2}\\ $$

なお、流体力学では質量を体積で割ったものである「密度」を用いると取り扱いやすくなります。

流体の密度を$\rho$、単位質量当たりの$\boldsymbol{F_p}, \, \boldsymbol{F_v}, \, \boldsymbol{F_g}$をそれぞれ$\boldsymbol{f_p}, \, \boldsymbol{f_v}, \, \boldsymbol{f_g}$と置くと、式（２）は以下のようになります。

$$ \rho \frac{D\boldsymbol{v}}{Dt} = \rho \boldsymbol{f_p} + \rho \boldsymbol{f_v} + \rho \boldsymbol{f_g} \tag{3}\\ $$

一般的には、式（３）の各項に具体的な式をいれたものをナビエ・ストークス方程式と呼びます。

カヲル

式（３）右辺の$\rho \boldsymbol{f}$は、単位体積あたりの力を示しているよ。

流体の加速度

多変数関数の微分

１変数関数の微分【高校数学のおさらい】

高校で習った微分は下式のように$x$を変数とする関数$f(x)$を微分するものでした。

$$ \frac{df(x)}{dx} \equiv \lim_{\Delta x \to 0} \frac{f(x + \Delta x) \, -\, f(x)}{\Delta x} \tag{4} $$

これは変数が$x$ただ1つなので、「1変数関数の微分」と呼ばれ、関数$f(x)$が描くグラフ上の曲線の点$\left( x, \, f(x) \right)$における接線の傾きに相当します。

２変数関数の微分 – 偏微分

大学以降では変数が2つ以上ある「多変数関数の微分」も扱います。

カヲル

本記事では変数が増えても計算の仕方は変わらないため、2変数関数の微分について解説するよ！

まず、$z = f(x, \, y)$という2変数関数について考えます。

$x$と$y$はそれぞれ値を少し動かすとグラフ上での傾きは変化しますが、ここで紹介する偏微分（Partial derivative）は$x$または$y$のみ動かした際の傾きを求めるものです。

$x$を微小変化させた際の$z$の変化

$$ \frac{\partial z}{\partial x} \equiv \lim_{\Delta x \to 0} \frac{f(x + \Delta x, \, y) \, -\, f(x, \, y)}{\Delta x} \tag{5} \\ $$

$y$を微小変化させた際の$z$の変化

$$ \frac{\partial z}{\partial y} \equiv \lim_{\Delta y \to 0} \frac{f(x, \, y+ \Delta y) \, -\, f(x, \, y)}{\Delta y} \tag{6} $$

上記の$\frac{\partial z}{\partial x}$や$\frac{\partial z}{\partial y}$が偏微分になります。

計算方法

$\frac{\partial z}{\partial x}$は$y$が固定されているので、$y$を定数として$x$について微分。
$\frac{\partial z}{\partial y}$は$x$が固定されているので、$x$を定数として$y$について微分。

２変数関数の微分 – 全微分

偏微分は1つの変数のみ微分しましたが、全微分は全ての変数を微分するものです。

2変数関数$f(x, \, y)$の全微分は以下のように定義されます。

$$ df(x, \, y) \equiv f(x + dx, \, y + dy) \, -\, f(x, \, y) \tag{7} $$

これは、先ほどの偏微分を用いて以下のように計算できます。

計算方法

$$ df = \frac{\partial f}{\partial x}dx + \frac{\partial f}{\partial y}dy \tag{8} \\ $$

リンク

流体の加速度（物質微分）

流体力学では、流体の運動を考える際に流体は無数の微小な塊から出来ていると考えます。

この微小な流体の塊を流体粒子（Fliud particle）または流体要素（Fluid element）と言います。

流体の運動を記述する方法には以下の２つがあります。

ラグランジュ（Lagrange）の方法
質点系の運動と同様に、各流体粒子に着目し、時間の経過と共に流体粒子がどのように動くか追跡していく方法。

この方法は、１つの流体粒子の経路や加速度を知る上では便利だが、全体の流れの様子を知るには適さない。
オイラー（Euler）の方法
特定の流体粒子を追跡するのではなく、流れ場全体の様子をそれぞれの時刻ごとに調べる方法。

流体力学では、１つの流体粒子の運動は一般的には興味の対象ではなく、空間に固定されたある点での圧力、流速の時間変化を知りたいため、この方法が一般に用いられる。

本記事ではオイラーの方法にて流体の加速度を考えることにします。

オイラーの方法では、空間に固定されたある点での流速を扱うため、流速は位置$\boldsymbol{r}$と時間$t$の関数になります。

しかし、ニュートンの運動方程式を思い返してみると位置$\boldsymbol{r}$は独立な変数ではなく、位置$\boldsymbol{r}$は時間$t$の関数になっているため、位置は$\boldsymbol{r}(t)$と表されます。

よって、流速は$\boldsymbol{v} \left(t, \, \boldsymbol{r}(t) \right)$と表されます。

ここでさらに、流速$\boldsymbol{v}$を時間$t$で微分し、加速度を求めます。

位置ベクトル$\boldsymbol{r}(t)$は$\left( x(t), \, y(t), \, z(t) \right)$と成分を分解し、$x, \, y, \, z$方向の流速を$v_x, \, v_y, \, v_z$と置くと、加速度$\boldsymbol{a}$は以下のようになります。

$$\begin{eqnarray} \boldsymbol{a} &=& \frac{d}{dt}\boldsymbol{v}\left(t, \, \boldsymbol{r}(t) \right) \\ \\ &=& \frac{d}{dt}\boldsymbol{v}\left(t, \, x(t), \, y(t), \, z(t) \right) \\ \\ &=& \begin{bmatrix} \frac{d}{dt}v_x \left(t, \, x(t), \, y(t), \, z(t) \right) \\ \frac{d}{dt}v_y \left(t, \, x(t), \, y(t), \, z(t) \right) \\ \frac{d}{dt}v_z \left(t, \, x(t), \, y(t), \, z(t) \right) \\ \end{bmatrix} = \begin{bmatrix} a_x \\ a_y \\ a_z \\ \end{bmatrix} \tag{9} \end{eqnarray}$$

まず、$x$成分の加速度$a_x$について求めると、多変数関数の微分（全微分）より

$$\begin{eqnarray} a_x &=& \frac{d v_x \left(t, \, x(t), \, y(t), \, z(t) \right)}{dt} \\ \\ &=& \frac{\frac{\partial v_x} {\partial t}dt + \frac{\partial v_x}{\partial x}dx + \frac{\partial v_x}{\partial y}dy + \frac{\partial v_x}{\partial z}dz }{dt} \\ \\ &=& \frac{\partial v_x} {\partial t} + \frac{\partial v_x}{\partial x}\frac{dx}{dt} + \frac{\partial v_x}{\partial y}\frac{dy}{dt} + \frac{\partial v_x}{\partial z}\frac{dz}{dt} \tag{10} \end{eqnarray}$$

速度の定義より、$\frac{dx}{dt}, \, \frac{dy}{dt}, \, \frac{dz}{dt}$を$v_x, \, v_y, \, v_z$と書き換えると

$$ a_x = \frac{\partial v_x}{\partial t} + v_x\frac{\partial v_x}{\partial x} + v_y\frac{\partial v_x}{\partial y} + v_z\frac{\partial v_x}{\partial z} \tag{11} $$

同様に$a_y, \, a_z$についても求めると、以下のようになります。

$$ \begin{bmatrix} a_x \\ a_y \\ a_z \\ \end{bmatrix} = \begin{bmatrix} \frac{\partial v_x}{\partial t} + v_x\frac{\partial v_x}{\partial x} + v_y\frac{\partial v_x}{\partial y} + v_z\frac{\partial v_x}{\partial z} \\ \frac{\partial v_y}{\partial t} + v_x\frac{\partial v_y}{\partial x} + v_y\frac{\partial v_y}{\partial y} + v_z\frac{\partial v_y}{\partial z} \\ \frac{\partial v_z}{\partial t} + v_x\frac{\partial v_z}{\partial x} + v_y\frac{\partial v_z}{\partial y} + v_z\frac{\partial v_z}{\partial z} \\ \end{bmatrix} \tag{12} $$

ここで、上式の左辺を以下のように記号を書き換えます。

$$ \begin{bmatrix} \frac{D}{Dt}v_x \\ \frac{D}{Dt}v_y \\ \frac{D}{Dt}v_z \\ \end{bmatrix} = \begin{bmatrix} \frac{\partial v_x}{\partial t} + v_x\frac{\partial v_x}{\partial x} + v_y\frac{\partial v_x}{\partial y} + v_z\frac{\partial v_x}{\partial z} \\ \frac{\partial v_y}{\partial t} + v_x\frac{\partial v_y}{\partial x} + v_y\frac{\partial v_y}{\partial y} + v_z\frac{\partial v_y}{\partial z} \\ \frac{\partial v_z}{\partial t} + v_x\frac{\partial v_z}{\partial x} + v_y\frac{\partial v_z}{\partial y} + v_z\frac{\partial v_z}{\partial z} \\ \end{bmatrix} \tag{13} $$

上式の時間微分$\frac{D}{Dt}$は、流体の運動に沿う微分（Differentiation following the motion of fluid）、物質微分（Material derivative）や実質微分（Substantial derivative）などと呼ばれます。

ここで、$\nabla$という記号で表される演算子であるナブラ演算子を定義します。

$x$方向、$y$方向、$z$方向の単位ベクトル（大きさ１のベクトル）をそれぞれ$\boldsymbol{e_x}, \, \boldsymbol{e_y}, \, \boldsymbol{e_z}$と置くと、ナブラ演算子は以下で定義されます。

$$ \begin{eqnarray} \nabla &\equiv& \frac{\partial}{\partial x}\boldsymbol{e_x} + \frac{\partial}{\partial y}\boldsymbol{e_y} + \frac{\partial}{\partial z}\boldsymbol{e_z} \\ \\ &=& \left( \frac{\partial}{\partial x}, \, \frac{\partial}{\partial y}, \, \frac{\partial}{\partial z} \right) \tag{14} \\ \end{eqnarray} $$

式（１３）中の各式にて$v_x, \, v_y, \, v_z$と$\nabla$はベクトルの内積のような形になっているので、$\left( \boldsymbol{v} \cdot \nabla \right)$と書き換えることができます。

よって、

$$ \begin{bmatrix} \frac{D}{Dt}v_x \\ \frac{D}{Dt}v_y \\ \frac{D}{Dt}v_z \\ \end{bmatrix} = \begin{bmatrix} \frac{\partial}{\partial t}v_x + \left( \boldsymbol{v} \cdot \nabla \right) v_x \\ \frac{\partial}{\partial t}v_y + \left( \boldsymbol{v} \cdot \nabla \right) v_y \\ \frac{\partial}{\partial t}v_z + \left( \boldsymbol{v} \cdot \nabla \right) v_z \\ \end{bmatrix} \tag{15} $$

と書き換えることができます。さらに、各成分をまとめると以下のようなベクトルの式で表すことができます。

$$ \frac{D \boldsymbol{v}}{Dt} = \frac{\partial \boldsymbol{v}}{\partial t} + \left( \boldsymbol{v} \cdot \nabla \right) \boldsymbol{v} \\ \tag{16} $$

カヲル

ナブラ演算子について詳しく知りたい方は「ベクトル解析」を勉強してみてね！

リンク

流体に働く力

この節では、式（３）右辺の単位体積あたりの「圧力による力」と「粘性力」について解説します。

単位体積あたりの圧力による力

いま、以下のように流体を微小六面体（流体粒子）として考えてみます。

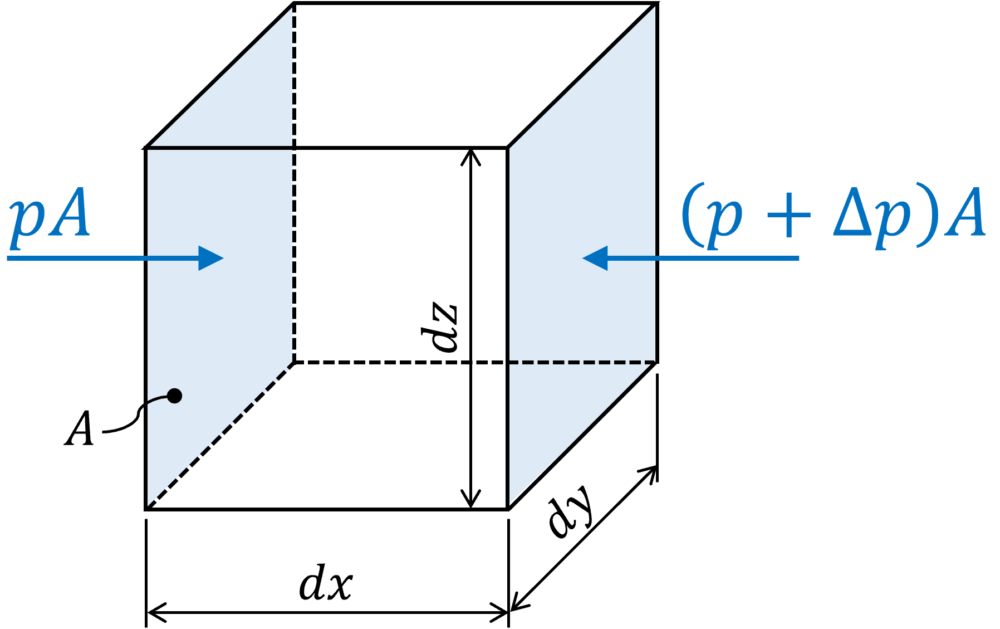
このとき、六面体の面積$A$の左側側面に圧力$p$がかかっているものとすると、左側側面にかかる力は$pA$となります。

一方、右側に$dx$進んだ右側側面では左側側面と微小に圧力が変化している筈です。

この圧力の変化分を$\Delta p$と置くと、右側側面にかかる力は$\left( p + \Delta p \right) A$となります。よって、この六面体（流体粒子）の$x$方向にかかる合力$F_{px}$は以下のようになります。

$$ \begin{eqnarray} F_{px} &=& pA \,-\, \left( p + \Delta p \right) A \\ \\ &=& \,-\, \Delta p A \tag{17} \\ \end{eqnarray} $$

ここで、左側側面から右側側面に向かって$x$方向に進むときの圧力の変化率は圧力$p$を微分することで求まります。

このとき、$x$方向の$p$の変化率だけを見ればよいため、$p$を$x$で偏微分した$\frac{\partial p}{\partial x}$にて求めることができます。

カヲル

縦軸に圧力$p$、横軸に$x$としたグラフを思い浮かべてみると、変化率はグラフ上での「傾き」に相当するよ。

よって、傾きに$x$の増加量$dx$を掛けたものが$y$の増加量、すなわち$dp$となるので、

$$ \Delta p \approx dp = \frac{\partial p}{\partial x} dx \tag{18} \\ $$

となります。式（１７）に式（１８）を代入し、$A$は図より$dy\,dz$であることを考えると以下のようになります。

$$ \begin{eqnarray} F_{px} &=& \,-\, \frac{\partial p}{\partial x} dx \, A \\ \\ &=& \,-\, \frac{\partial p}{\partial x} dx \, dy \, dz \tag{19} \\ \end{eqnarray} $$

ここで、式（１９）の$dx\,dy\,dz$は微小六面体（流体粒子）の体積を表しているため、$x$方向の単位体積あたり力は$\,-\, \frac{\partial p}{\partial x}$となります。

よって、$y$方向、$z$方向も同等に求めると、式（３）右辺の単位体積あたりの圧力による力$\rho \boldsymbol{f_p}$は

$$ \rho \boldsymbol{f_p} = \left( \,-\, \frac{\partial p}{\partial x}, \,-\, \frac{\partial p}{\partial y}, \,-\, \frac{\partial p}{\partial z} \right) \tag{20} \\ $$

となります。式（２０）はベクトル解析における勾配（Gradient）の定義より、以下のように表すこともできます。

$$ \rho \boldsymbol{f_p} = -\nabla p \tag{21} $$

リンク

単位体積あたりの粘性力

ニュートンの粘性法則

流体の中を運動する物体は、流体から運動を妨げようとする抵抗力が働きます。この流体の変形に対して抵抗を示す性質を粘性（Viscosity）と言います。

流体の粘性は、流体の速度が流れに対して垂直に変化するとき、つまり速度勾配を持つときに流れに沿って平行な面に沿って応力（単位面積あたりの力）が生じる性質と定義されます。

カヲル

この平行に働く応力をせん断応力（Shear stress）と言うよ。

ここで、下図のように２つの長い平行平板間の流体の運動について考えてみましょう。

この平板間の距離$h$は小さく、下側の平板は静止（速度$V_1$はゼロ）で上側の平板は速度$V_2$の一定速度で移動しているものとします。

このとき、流体は粘性（抵抗力）を持っているので、上側の移動平板境界部における流体の速度は$V_2$となり、下側の固定平板境界部における流体の速度はゼロとなります。

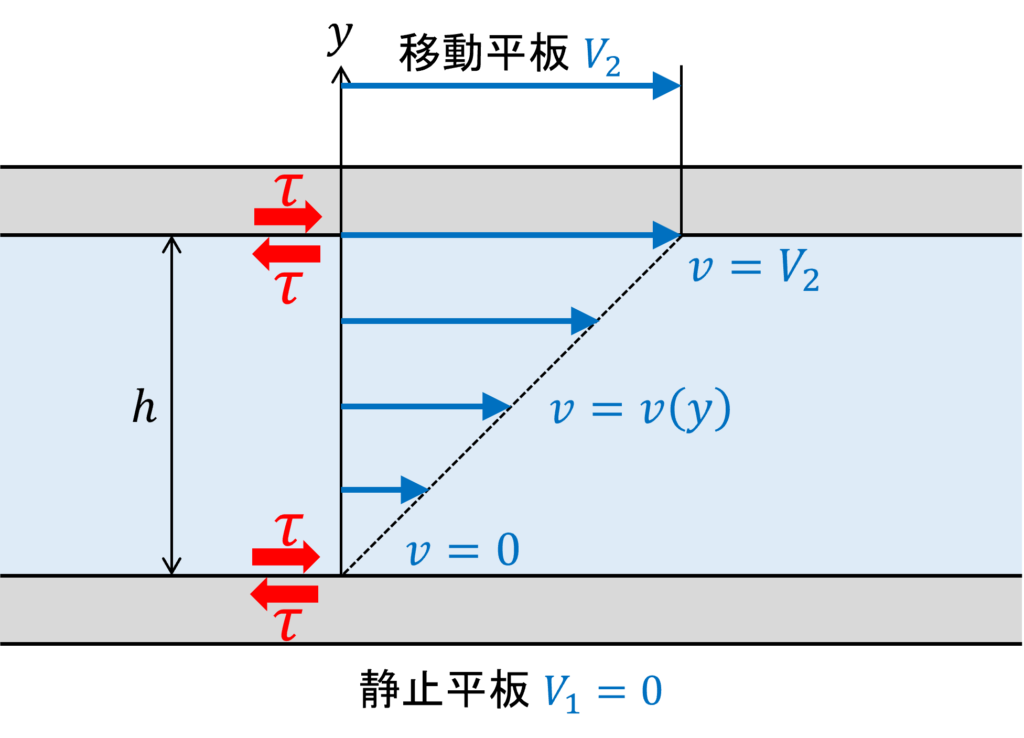
このとき、流体の速度$v$が遅く、層状に流れているとき（層流のとき）は以下の式が成り立ちます。

$$ v(y) = \frac{V_2}{h}y \tag{22} $$

また、このとき平板に単位面積あたりに働く接線力、すなわちせん断応力$\tau$は以下のようになります。

$$ \tau = \mu \frac{V_2}{h} \tag{23} \\ $$

上式の比例定数$\mu$は、粘性係数（Coefficient of viscosity）と呼ばれます。

カヲル

平板間の距離$h$が小さいほどせん断応力（単位面積あたりの抵抗力）が大きく、移動平板の速度$V_2$が大きいほどせん断応力が大きくなるよ！

ここで、式（２３）を流れの中の任意の速度勾配についても適用できるようにすると以下のようになります。

$$ \tau = \mu \frac{dv}{dy} \tag{24} $$

上式はニュートンの粘性法則（Newton’s law of viscosity）と呼ばれています。

せん断応力の一般形の式

カヲル

ここまでは平行平板でのせん断応力について見てきたけど、今度は圧力による力を求めた際と同様に微小六面体（流体粒子）に適用できる形で見ていこう！

いま、微小六面体（流体粒子）に働くせん断応力を$\tau_{ij}$と書くことにします。１つ目の添え字$i$は面を指定するものとし、２つ目の添え字$j$は方向を指定するものとします。

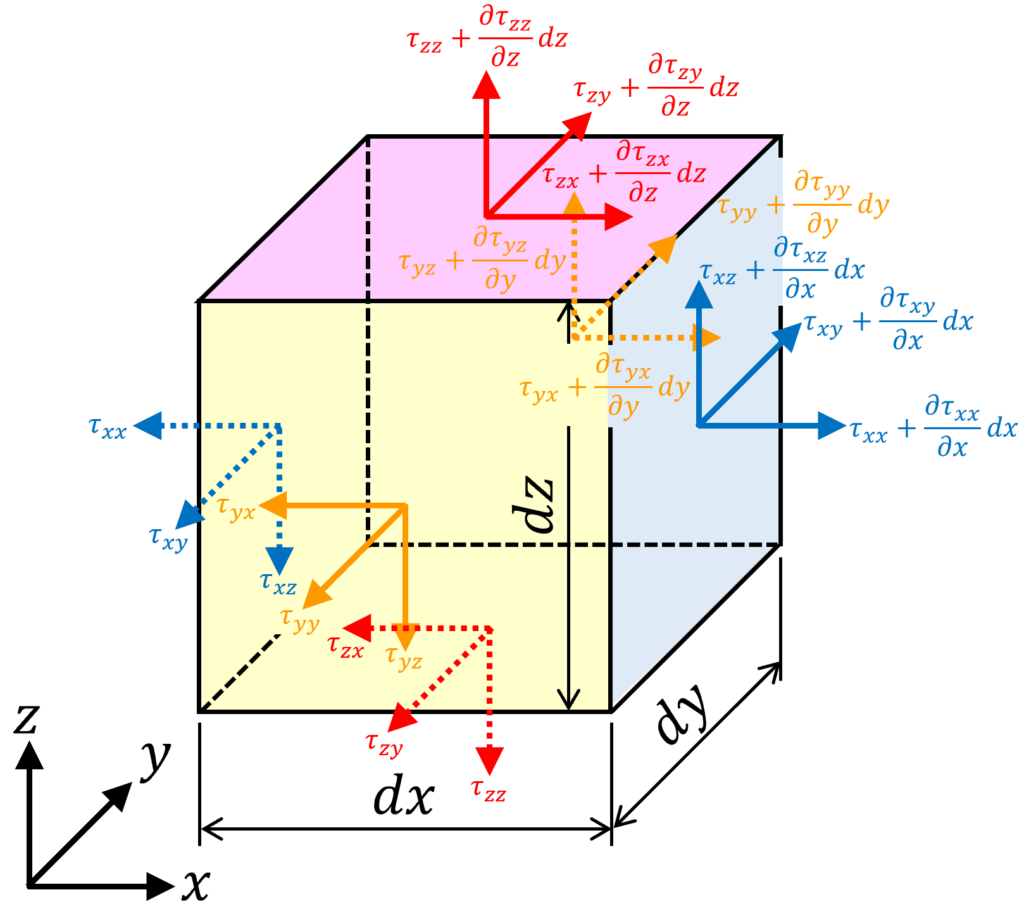
本記事では証明は省略しますが、各軸のモーメントのつり合いを考えた際にせん断応力には以下のような対称性があります。

$$ \tau_{ij} = \tau_{ji} \tag{25} $$

さらに、式（２４）を微小六面体（流体粒子）に適用できるように一般化すると以下のようになります。

$$ \begin{equation} \left\{ \, \begin{aligned} &\tau_{xx} = 2\mu \frac{\partial v_x}{\partial x} \\ &\tau_{yy} = 2\mu \frac{\partial v_y}{\partial y} \\ &\tau_{zz} = 2\mu \frac{\partial v_z}{\partial z} \\ &\tau_{xy} = \tau_{yx} = \mu \left( \frac{\partial v_x}{\partial y} + \frac{\partial v_y}{\partial x} \right) \\ &\tau_{yz} = \tau_{zy} = \mu \left( \frac{\partial v_y}{\partial z} + \frac{\partial v_z}{\partial y} \right) \\ &\tau_{zx} = \tau_{xz} = \mu \left( \frac{\partial v_z}{\partial x} + \frac{\partial v_x}{\partial z} \right) \end{aligned} \right. \tag{26} \end{equation} $$

リンク

単位体積あたりの粘性力

以上の内容をもとに流体に働く粘性力について考えてみましょう。

fig. 3を見ながら$x$成分について書きだすと、せん断力はせん断応力に面積を掛けたものとなるので、

$$ \begin{eqnarray} &&\left\{\,-\, \tau_{xx} + \left( \tau_{xx} + \frac{\partial \tau_{xx}}{\partial x}dx \right) \right\} dydz +\left\{\,-\, \tau_{yx} + \left( \tau_{yx} + \frac{\partial \tau_{yx}}{\partial y}dy \right) \right\} dxdz +\left\{\,-\, \tau_{zx} + \left( \tau_{zx} + \frac{\partial \tau_{zx}}{\partial z}dy \right) \right\} dydx \\ \\ &&=\frac{\partial \tau_{xx}}{\partial x}dxdydz +\frac{\partial \tau_{yx}}{\partial y}dydxdz +\frac{\partial \tau_{zx}}{\partial z}dydydx \\ \\ &&= \left(\frac{\partial \tau_{xx}}{\partial x} +\frac{\partial \tau_{yx}}{\partial y} +\frac{\partial \tau_{zx}}{\partial z} \right) dxdydz \tag{27} \\ \end{eqnarray} $$

となります。ここで、$dxdydz$は微小六面体の体積を表しているので、上式を$dxdydz$で割って単位体積あたりの力とし、式（２６）を代入すると

$$ \begin{eqnarray} &&\frac{\partial}{\partial x} \tau_{xx} +\frac{\partial}{\partial y} \tau_{yx} +\frac{\partial}{\partial z} \tau_{zx} \\ \\ &&=\frac{\partial}{\partial x} \left\{ 2\mu \frac{\partial v_x}{\partial x} \right\} +\frac{\partial}{\partial y} \left\{\mu \left( \frac{\partial v_x}{\partial y} + \frac{\partial v_y}{\partial x} \right) \right\} +\frac{\partial}{\partial z} \left\{\mu \left( \frac{\partial v_z}{\partial x} + \frac{\partial v_x}{\partial z} \right) \right\} \\ \\ &&=\mu \left(\frac{\partial^2 v_x}{\partial x^2} + \frac{\partial^2 v_x}{\partial y^2} + \frac{\partial^2 v_x}{\partial z^2} \right) + \mu \frac{\partial}{\partial x} \left(\frac{\partial v_y}{\partial x} + \frac{\partial v_z}{\partial y} + \frac{\partial v_x}{\partial z} \right) \tag{28} \\ \\ \end{eqnarray} $$

上式はベクトル解析におけるラプラシアン（Laplacian）と発散（Divergence）の定義より、以下のように表すこともできます。

$$ \mu \nabla^2 v_x + \mu \frac{\partial}{\partial x} \left( \nabla \cdot \boldsymbol{v} \right) \tag{29} \\ $$

ここで、非圧縮性流体では$\nabla \cdot \boldsymbol{v} = 0$となるため、

$$ \mu \nabla^2 v_x \tag{30} \\ $$

となります。$y$成分、$z$成分も同様であるため、単位体積あたりの粘性力$\rho \boldsymbol{f_v}$は以下のようになります。

$$ \rho \boldsymbol{f_v} = \mu \nabla^2 \boldsymbol{v} \tag{31} \\ $$

ナビエ・ストークス方程式の導出

以上より、非圧縮性流体のナビエ・ストークス方程式は式（３）に式（１６）、式（２１）、式（３１）を代入し、以下のようになります。

$$ \rho \left\{ \frac{\partial \boldsymbol{v}}{\partial t} + \left( \boldsymbol{v} \cdot \nabla \right) \boldsymbol{v} \right\} = -\nabla p + \mu \nabla^2 \boldsymbol{v} + \rho \boldsymbol{f_g} \tag{32}\\ $$