圧縮性流体での流量のサチレートを考慮した流量計算法【窒息流】

円管や平行平板間を流れる非圧縮性流体の流れでは、以前の記事にて紹介したポアズイユ流れの式で流量を計算することができました。

しかし、圧縮性流体の場合は流路間の圧力差を大きくすると途中までは非圧縮性流体と同様に流量が増えていきますが、あるところで流量の増加がなくなります。（サチレートします）

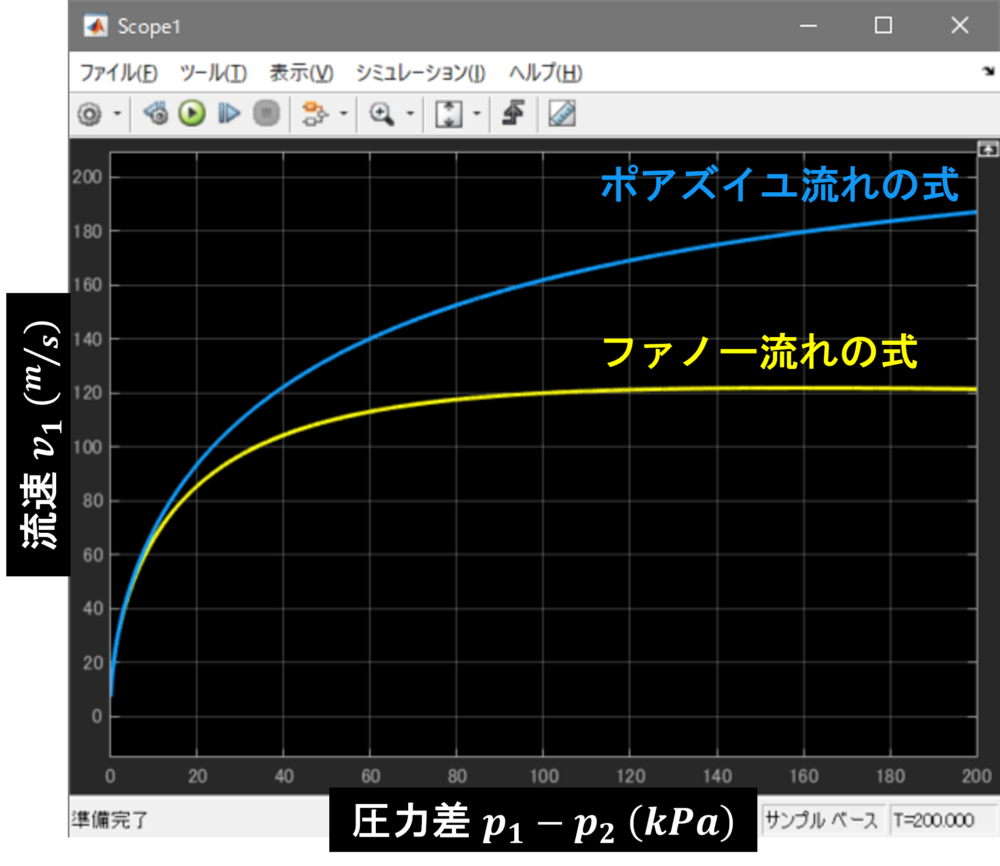
この流量（流速）がサチレートする流れをチョーク流れ（窒息流）と言います。

ファノー流れの式

本記事で紹介するファノー流れ（Fanno flow）の式は以下の条件を持っています。

上記の②に関して補足しますが、気体の圧縮性の影響が出る領域は流速が速くなっており、乱流になっていることが多いです。

層流の場合は壁面との距離に対して放物線状に流速が分布し緩やかに変化しますが、乱流の場合は壁面から離れると一気に流速が速くなります。

ファノー流れの式では乱流の領域での流れをメインに考えており、上記性質を利用して管路の断面で流速が一様になっていることを想定して求めた式になります。

カヲル

では、先ずは断面形状を固定せず、断面積一定の流れについて見ていこう。

下図のように断面積\(A\,(m^2)\)が一定の管路にて、断面１（圧力\(p_1\,(Pa\:abs.)\), 流速\(v_1\,(m/s)\), 密度\(\rho_1\,(kg/m^3)\)）から断面２（圧力\(p_2\,(Pa\:abs.)\), 流速\(v_2\,(m/s)\), 密度\(\rho_2\,(kg/m^3)\)）へ気体が流れている状態を考えます。

このとき、断面１と断面２の間の長さは\(L_p\,(m)\)となっており、流体と壁面が触れる長さ（濡れ縁の長さ）は\(L_w\,(m)\)となっているものとします。

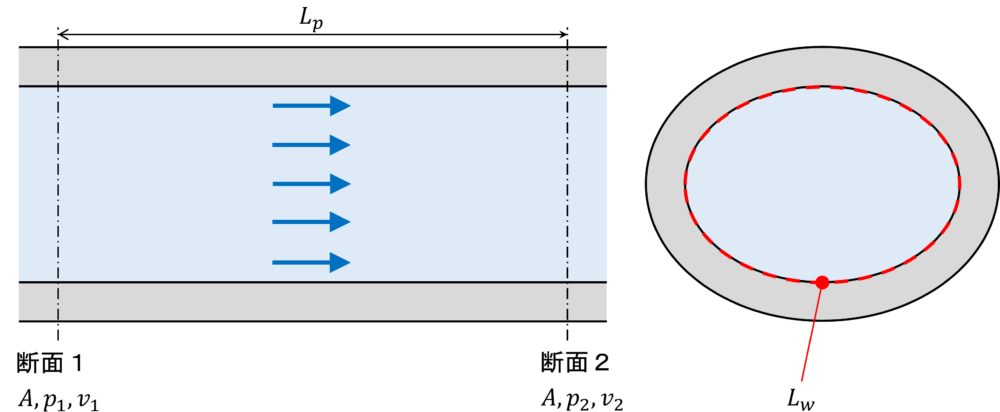
比熱比（空気の場合は1.4）を\(\kappa\)と置くと、流速\(v_1\)を求める式は以下のようになります。

ここで式（１）の\(f\)は粘性による壁面との摩擦（抵抗力）を示す係数で摩擦係数（ファニング摩擦係数, Fanning friction factor）と呼ばれます。

カヲル

壁面とのせん断応力を\(\tau_w\)と置くと、摩擦係数は\(f \equiv \frac{\tau_w}{\rho v^2/2}\)となるよ。

ただし、通常は実験や流体解析など、別の方法で\(f\)を求めるよ。

心太

形状が決まっても摩擦係数\(f\)は一定値ではないので、レイノルズ数（Reynolds number）で整理すると一本のグラフにすることができますね。

なお、工業的には断面積一定の円管は広く使われており、式（１）を内径\(D\,(m)\)の円管の場合に限定すると以下のようになります。

心太

式（２）より体積流量\(\dot{V_1}\,(m^3/s)\)と質量流量\(\dot{m_1}\,(kg/s)\)は以下のようになりますね。

\(\dot{V_1} = A v_1 \tag{3}\)

\(\dot{m_1} =\dot{m_2} = \rho_1 \dot{V_1} \tag{4}\)