二次元ポアズイユ流れの導出と紹介

こんにちは、カヲルです！

今回は二次元ポアズイユ流れの式の紹介とナビエ・ストークス方程式からの導出について書きたいと思います。

今回からちょっとした小ネタもブログに載せていきたいと思います！

二次元ポアズイユ流れ

二次元ポアズイユ流れの式は比較的距離の近い二つの平板間に流れる空気や水などの流量を求めるときに用いられます。

本記事は流体力学の基礎を理解している必要がありますが、簡単に流体力学の概要を述べたあとにメインの式の導出に入りたいと思います。

流体力学とは

空気、天然ガス、水、オイル、ガソリンなどに代表される気体（Gas）と液体（Liquid）を総称して流体（Fluid）と言います。

流体の特徴として固体（Soild）と比べてわずかな力で変形し、運動する性質を持っています。

この運動を流体の流れと言い、自動車のボデーや飛行機の翼の周りの流れなど物体の外部の流れを外部流れ（External flow）、配管やターボ機械などの内部の流れを内部流れ（Internal flow）と言います。

流体力学（Fluid dynamics）はこれらの流れの挙動を解析する学問になります。

ナビエ・ストークス方程式

流体力学も物理学分野の一つですが、物理法則を数学的な方程式で書き表したものを支配方程式（Governing equation）または基礎方程式と言います。

例えば力学でいうニュートンの運動方程式、電磁気学のマクスウェル方程式がそれに当たります。

ナビエ・ストークス方程式（Navier–Stokes equations）は流体の運動を記述するためにニュートンの運動方程式を変形したものになります。

密度一定（非圧縮性）、粘性係数一定（等質）の場合のナビエ・ストークス方程式は下記のようになります。

カヲル

流速（Flow velocity）は流れの速さ、密度（Density）は単位体積あたりの質量のことだよ。

粘性（Viscosity）は流体中を運動する物体が流体から運動を妨げようとする抵抗力のことを言うよ。

流体力学のもう一つの支配方程式：連続の式

2022年7月1日流体力学「連続の式」ってなんだろう？

全微分・偏微分おさらい

2022年6月21日多変数関数の微分のイメージを掴もう！

二次元ポアズイユ流れ

ナビエ・ストークス方程式は数学的には２階非線形偏微分方程式となっています。

微分方程式は非線形であると段違いに解くのが難しくなり、２１世紀現在では数式変形のみで解くことができていないものになっています。（有限回の数式変形のみで微分方程式を解くことを解析的に解くと言います）

よってこの方程式を解く場合はコンピュータを使った数値計算によって近似的に解く形になりますが、いくつかの制限（境界条件）を設けることで解ける形にすることが出来ます。

カヲル

ナビエ・ストークス方程式を解くことはアメリカのクレイ数学研究所が２０００年に発表した7つの問題（ミレニアム懸賞問題）の１つとなっていて100万ドルの懸賞金がかけられているよ。是非挑戦してね！（笑）

ここでは制限を設けて解ける形にしたものの一つである二次元ポアズイユ流れ（Two-Dimensional Poiseuille Flow）について紹介したいと思います。

二次元ポアズイユ流れは比較的距離が近い間隔h（m）の２枚の平行な平板がそれぞれ速度V1、V2（m/s）で運動するとき、その間を流れる密度一定の定常流れのことを言います。

では、まず下図のようにx軸とy軸をとります。ここで流れは層流の条件とし速度のy方向成分は無視（ゼロ）できるものとします。また、重力などの外力も無視できるものとします。

カヲル

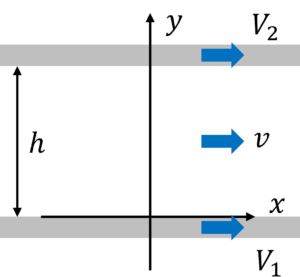
定常流れ（Steady flow）とはすべての場所で圧力、速度、密度などの物理量が時間変化しない流れを言うよ。

層流（Laminar flow）は流れ方向に向かって規則正しく流れているものを言い、反対に渦のように様々な方向に不規則に流れいるものを乱流（Turbulence）と言うよ。

前項で記載したナビエ・ストークス方程式はベクトルの方程式となっており、３本の方程式がまとめられた形になっています。これをx成分とy成分のみ取り出すと下式になります。

$$\begin{eqnarray} \fbox{x成分} \, \ \rho \left( \frac{\partial v_x}{\partial t} \ + \ v_x \frac{\partial v_x}{\partial x} \ + \ v_y \frac{\partial v_x}{\partial y} \right) &=& – \frac{\partial p}{\partial x} + \mu \left( \frac{\partial^2 v_x}{\partial x^2} \ + \ \frac{\partial^2 v_x}{\partial y^2} \right) + \rho f_x \tag{1} \\ \fbox{y成分} \ \ \rho \left( \frac{\partial v_y}{\partial t} \ + \ v_x \frac{\partial v_y}{\partial x} \ + \ v_y \frac{\partial v_y}{\partial y} \right) &=& – \frac{\partial p}{\partial y} + \mu \left( \frac{\partial^2 v_y}{\partial x^2} \ + \ \frac{\partial^2 v_y}{\partial y^2} \right) + \rho f_y \tag{2} \\ \end{eqnarray}$$

また、流体力学における質量保存の法則を下式のように書くことができます。この式を非圧縮性流体の連続の式（equation of continuity）と言います。

$$ \nabla \cdot \mathbf{v} = 0 \tag{3} $$

今回の条件ではx方向の速度v（m/s）の分布は同一であるとすると

$$ \frac{\partial v_x}{\partial x} = 0 \tag{4} $$

となり、流れの加速度は

$$ v_x \frac{\partial v_x}{\partial x} = 0 \tag{5} $$

となります。以上より式（１）、（２）のナビエ・ストークス方程式は簡略化されて

$$\begin{eqnarray} \fbox{x成分} \, \ \frac{\partial p}{\partial x} &=& \mu \frac{d^2 v_x}{d y^2} \tag{6} \\ \fbox{y成分} \ \ \frac{\partial p}{\partial y} &=& 0 \tag{7} \end{eqnarray}$$

となります。式（４）と式（７）よりvxはyのみ、pはxのみの関数となります。よって、式（６）の偏微分方程式は常微分方程式の形に書き換えて

$$ \frac{dp}{dx} = \mu \frac{d^2 v_x}{d y^2} \tag{8} $$

となります。ここで式（８）を

$$ \frac{d}{dy} \left( \frac{dv_x}{dy} \right) = \frac{1}{\mu} \frac{dp}{dx} \tag{9} $$

と式変形し、yで積分すると

$$\begin{eqnarray} \int \frac{d}{dy} \left( \frac{dv_x}{dy} \right) dy &=& \int \frac{1}{\mu} \frac{dp}{dx} dy \\ \to \int d \left( \frac{dv_x}{dy} \right) &=& \frac{1}{\mu} \color{blue}{\frac{dp}{dx}} \int dy \\ \to \frac{dv_x}{dy} &=& \frac{1}{\mu} \frac{dp}{dx} y \ + \ C_1 \tag{10} \end{eqnarray}$$

となります。ここでCiは積分定数とします。式（１０）を変数分離し、積分すると

$$\begin{eqnarray} dv_x &=& \left( \frac{1}{\mu} \frac{dp}{dx} y \ + \ C_1 \right) dy \tag{11}\\ \int dv_x &=& \int \frac{1}{\mu} \frac{dp}{dx} y \, dy \ + \ \int C_1 \, dy \\ \to v_x &=& \frac{1}{2 \mu} \frac{dp}{dx} y^2 \ + \ C_1 y \ + \ C_2 \tag{12} \end{eqnarray}$$

となります。ここでy = 0のとき、vx = V1という境界条件を与えると

$$C_2 \ = \ V_1 \tag{13}$$

となります。式（１２）に式（１３）を代入し、同様にy = hのとき、vx = V2という境界条件を与えると

$$\begin{eqnarray} V_2 &=& \frac{1}{2 \mu} \frac{dp}{dx} h^2 \ + \ C_1 h \ + \ V_1 \\ \to C_1 &=& \frac{V_2 \ – \ V_1}{h} \ – \ \frac{1}{2 \mu} \frac{dp}{dx} h \tag{14} \end{eqnarray}$$

となります。ここで問題設定からvxをvと置き換え、式（１２）に式（１３）、（１４）を代入すると

$$\begin{eqnarray} v &=& \frac{1}{2 \mu} \frac{dp}{dx} y^2 \ + \ \left( \frac{V_2 \ – \ V_1}{h} \ – \ \frac{1}{2 \mu} \frac{dp}{dx} h \right) y \ + \ V_1 \\ &=& V_1 \ + \ \frac{V_2 \ – \ V_1}{h} y \ – \ \frac{1}{2 \mu} \frac{dp}{dx} ( yh \ – \ y^2 ) \\ &=& V_1 \ + \ \frac{V_2 \ – \ V_1}{h} y \ – \ \frac{h^2}{2 \mu} \frac{dp}{dx} \left\{ \frac{y}{h} \ – \ \left( \frac{y}{h} \right)^2 \right\} \tag{15} \end{eqnarray}$$

となります。また、yで積分し、単位長さ当たりの体積流量qを求めると

$$\begin{eqnarray} q &=& \int_0^{h} v \, dy \\ &=& \left[ V_1 y \, + \, \frac{V_2 \, – \, V_1}{h} \frac{y^2}{2} \, – \, \frac{h^2}{2 \mu} \frac{dp}{dx} \left\{ \frac{y^2}{2h} \, – \, \frac{y^3}{3h^2} \right\} \right]_0^h \\ &=& V_1 h \, + \, (V_2 \, – \, V_1) \frac{h}{2} \, – \, \frac{h^3}{12 \mu} \frac{dp}{dx} \tag{16} \end{eqnarray}$$

となります。ここで式（１５）、（１６）にて両側の平板が固定（V1 = V2 = 0）されている場合を二次元ポアズイユ流れと言います。

リンク

活用例

前述の通り、ナビエ・ストークス方程式は一般には解析的に解けないため、例えば流体機械内部の狭い隙間を通る流れの計算（モデル化）などに応用できます。

また、FluentやSTAR-CCM+のような市販の熱流体解析ソフトの計算の確からしさ（物理モデルやメッシュ設定など）を確認するときなどに使えます。

まとめ

機械要素において比較的距離の近い二つの平板間の流れを簡単に計算したい場合も多いかと思います。

ベルヌーイの定理もナビエ・ストークス方程式に制約（境界条件）を設けて解いた形にはなっていますが、粘性の影響が考慮できないため不便なことも多いです。

そのようなときに上記の式を用いて計算してみては如何でしょうか。

2022年7月31日分かりやすく解説！人工知能、機械学習とは

2022年7月1日流体力学「連続の式」ってなんだろう？

2023年5月1日超・基礎から解説！ナビエ・ストークス方程式の導出【流体力学】

さらに流体力学を勉強されたい方向け参考書籍

マンガでわかる流体力学

リンク

内容（Amazonより）

マンガでビジュアルに流体力学が勉強できる！
好評の「マンガでわかる」シリーズに流体力学が登場。
流体の流れや力学のメカニズムをマンガとイラストを用いてビジュアルに説明しているため、文章だけではわかりにくかった部分が見えるように理解できる。
流体力学を学ぶ上で、数学や物理の基礎的な部分から様々な事象のメカニズムまでをやさしく丁寧に解説。また、多くの人が苦手とする重要公式についても、その成り立ちや展開を平易な説明とともに掲載しているので、無理なく学習できる。はじめて流体力学を学ぶ方、おさらいをしたい方に最適。

流体力学 (新物理学シリ-ズ)

リンク

内容（Amazonより）

目次/Ⅰ.流体の運動の一般論　1.流体と流体力学　2.流体の運動と力　3.流体の諸特性　4.流体力学の基礎方程式　Ⅱ.完全流体の運動　5.完全流体の運動の一般論　6.水の波　7.ポテンシャル流　8.2次元ポテンシャル流　9.渦運動　Ⅲ.圧縮性流体の運動10.音波と衝撃波　11.高速気流　Ⅳ.粘性流体の運動　12.粘性流の一般論　13.代表的な粘性流　14.遅い粘性流　15.境界層　Ⅴ.乱流　16.流れの安定性　17.乱流