こんにちは、カヲルです!
ゴムの構造解析(FEM)をする際に入力する物性値に困ったことはないでしょうか。
CAEでゴム部品の変位、反力、接触幅、接触面圧、応力などを求めたいときってありますよね?
ラフ検討のレベルであれば材料非線形で解析してもまずは問題ないことが多いので、ゴムの硬度からヤング率を換算できれば便利かと思います。
今回はゴムの硬度からヤング率を換算する方法について書きたいと思います。
非線形構造解析ではある構造物の変位と荷重の関係が線形(直線状)でないものを扱います。非線形になる主な要因としては大きく分けて材料非線形、幾何学的非線形、境界条件非線形の3つがあります。
1.材料非線形
材料非線形とは応力とひずみの関係が線形でないものを指します。例えば塑性、ひずみ速度に依存する弾塑性、クリープ、超弾性などがあります。
2.幾何学的非線形
外力が働いたときに形状が変化することで構造物の剛性が変化するものを指します。例えばアーチ状のものがペコっと座屈したときなどがあります。
3.境界条件非線形
構造解析では構造物に対して適切な境界条件(拘束条件や荷重条件)を与えますが、境界条件が解析の途中で変化するものを指します。例えば物体同士の接触は一般に荷重を増やしたときに接触する範囲(境界条件)が非線形的に増えますので境界条件非線形になります。
ゴムの硬度から構造解析(FEM)に入力する物性値を導こう!
構造解析を実施する際に必ず必要となるヤング率とポアソン比について見ていきます。
ポアソン比とは
構造解析を実施することが前提であれば、材料力学はある一定以上は理解していると思われますのでおさらいにはなってしまいますが、先ずはポアソン比の定義から見ていきたいと思います。
下図のように構造物に荷重を印加した場合、縦方向は縮み、横方向は伸びます。
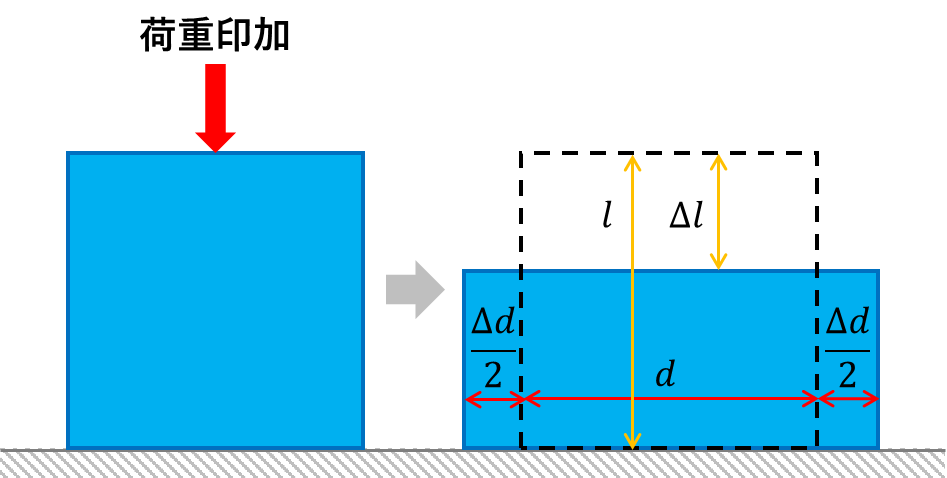
この時、縦方向の元の長さがl、縮んだ長さをΔlとするとこの比を縦ひずみε1という物理量で表すことができます。
同様に横方向の元の長さがd、伸びた長さをΔdとするとこの比を横ひずみε2という物理量ですことができます。なお、ここで縦と横は構造物の置いた方向に限らず、荷重印加方向を縦、荷重印加方向と垂直の方向を横と呼びます。また、例では圧縮荷重をかけていますが、引張荷重でも同様です。
この縦ひずみε1と横ひずみε2の比をポアソン比ν(Poisson’s ratio)と言います。

ポアソン比は金属材料では0.3前後の値をとるよ。また、ポアソン比は単位は無く、無次元量となるよ。
ゴム材料のポアソン比
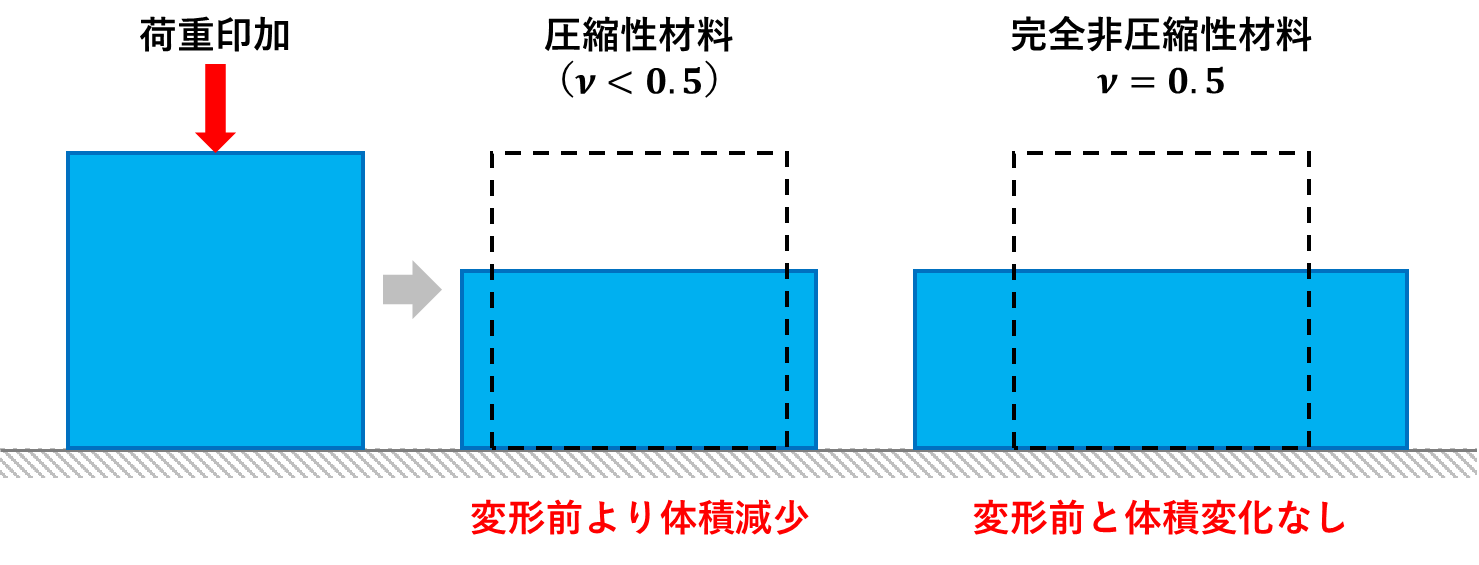
ここでゴム材料のポアソン比に入る前にゴム材料の特徴について書きます。ゴム材料の特徴として非圧縮性というものがあります。
これは下の図のように荷重をかけた際に体積が変化しない性質を言います。微小変形を仮定したとき、”完全”非圧縮性の材料ではポアソン比ν=0.5となります。

ゴム材料を構造解析する際はポアソン比ν=0.49程度の値を入力することが多いよ。
ヤング率とは
こちらもヤング率の定義からおさらいしていきます。
下図の構造物に荷重が印可された場合を考えます。
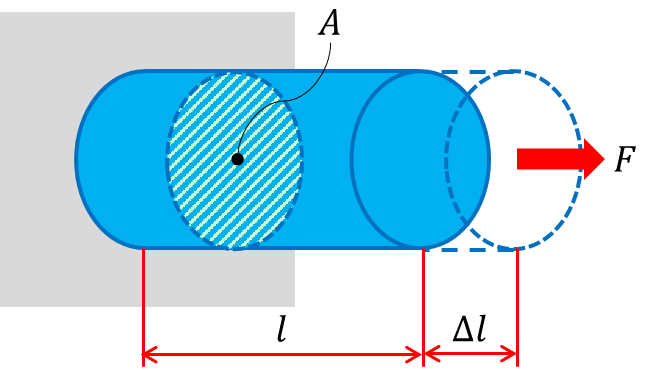
断面積Aの構造物に荷重(外力)Fを印加し、内力N(= F)がかかったとき、単位面積当たりの内力を応力σと言います。
また、ばねを考えたときに加えた荷重に対して変形量は変わるかと思います(フックの法則)。これをひずみと応力の関係に置き換えると下式のようになります。
このときの比例定数Eをヤング率(Young’s modulus)または縦弾性係数(modulus of longitudinal elasticity)と呼びます。
ここで上式を変形すると
となり、荷重が一定であれば
が成り立ちます。この式より構造物の変形のしにくさがヤング率であることが分かります。なお、ヤング率の”ヤング”は人名(Thomas Young)になります。ヤング率の単位はPaで金属材料では数百GPa、ゴム材料では数MPaとなります。
ゴム材料の硬度とは
次にゴムの硬度(国際ゴム硬さ)の定義についても見ていきます。
硬度計の原理は下図のようになっています。
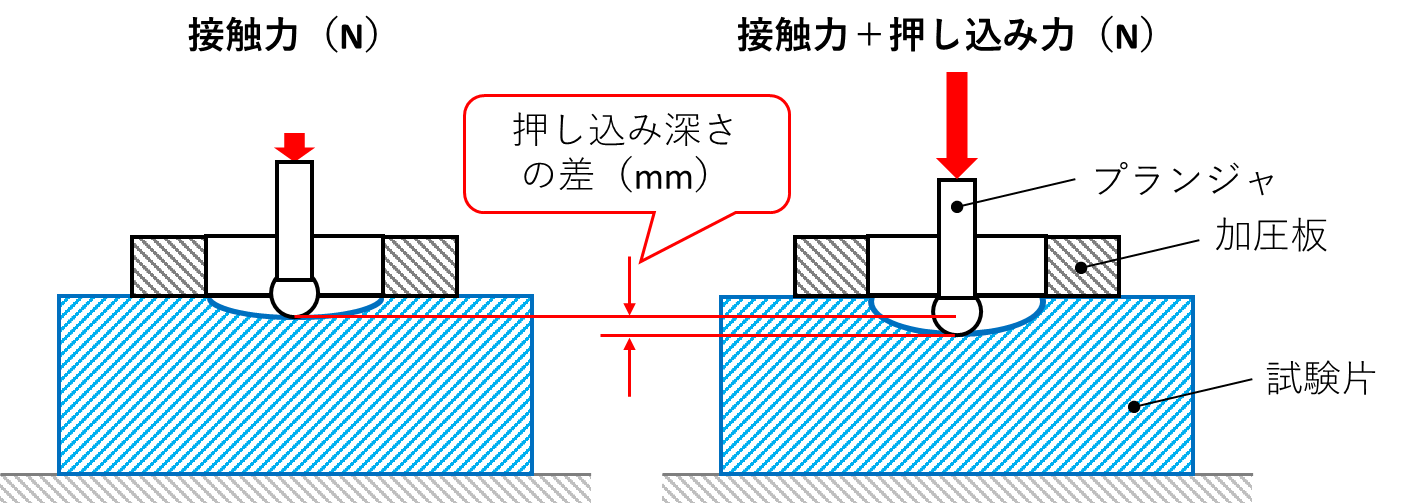
まず、先端が球形のプランジャに予め決められた接触荷重を印加するとゴムの試験片は凹みます。更に決められた押し込み力を印加すると更に試験片は凹みます。
ここで接触力と押し込み力の合計を合計押し込み力と言います。
このときの凹み量の増加量を”押し込み深さの差“と定義します。ゴムの硬度はプランジャの押し込み深さの差から定義されています。
例としてN法(プランジャの先端球の直径:2.5mm、接触力:0.3N、合計押し込み力5.7N)と呼ばれる試験法では押し込み深さの差と硬度の関係は下図のようになります。
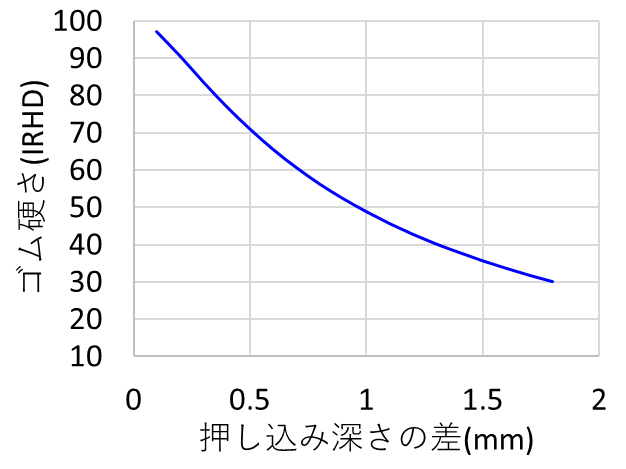
このように実質的にゴムの硬度は一定荷重を印加した際の変形量を測定しており、先ほど、ヤング率の説明で書いた変形量とヤング率の関係に似ています。
ゴムの硬度からヤング率を求める
ゴムの硬度を等方な完全弾性体と仮定した場合にヤング率と硬度の関係は下式が成り立つことが知られています。
(参考文献:Scott, J.R Physical Testing of Rubber. Maclaren and Sons, 1965)
ここでDは押し込み深さの差、Rは球の半径、fは接触力、Fは合計押し込み力、Eは加硫ゴムのヤング率となります。

上式をグラフにすると下図のようになるよ。
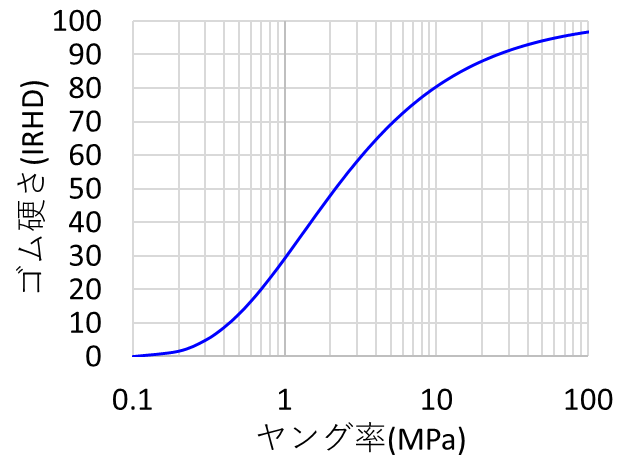
硬度からヤング率を換算するエクセルファイルはこちらよりダウンロードできます。
まとめ
ゴムは非圧縮性材料であることからポアソン比は0.49程度、ヤング率はゴムの硬度が押し込み力を加えた際の変形量(押し込み深さの差)であることから換算できることが分かりました。
海外調達部品などゴムの物性値はすぐ手に入らないことも多いと思いますので、構造解析(FEM)での初期検討で今回の方法が役に立つのではないでしょうか。
関連記事
構造解析(FEM)を勉強されたい方向け 参考書籍
著者略歴 (「BOOK著者紹介情報」より)
博士(工学)。S32年生まれ、大阪府出身。松下電器産業株式会社中央研究所勤務を経て、1993年京都大学工学部機械工学科助教授、2000年京都大学大学院工学研究科機械工学専攻教授、2003年同マイクロエンジニアリング専攻教授、2008年総長室長、2009年副理事。NPO法人CAE懇話会は、関西CAE懇話会設立時の発起人の一人として、幅広く活動。2002年より副理事長。特に解析塾では10年以上に渡り、延べ900名以上の受講生を指導する(本データはこの書籍が刊行された当時に掲載されていたものです)
著者略歴 (「BOOK著者紹介情報」より)
博士(工学)。京都大学大学院工学研究科修了。S36年生まれ。大阪市出身。株式会社IDAJ勤務。非線形有限要素法プログラムのカスタマーサポートを経て、非線形解析の受託解析業務に従事。2001年から、NPO法人CAE懇話会の解析塾において非線形構造解析コースを担当。延べ300名以上の受講生を指導する。2006年より、日本ゴム協会・ゴムの力学研究分科会の書記を担当(本データはこの書籍が刊行された当時に掲載されていたものです)
内容(Amazon商品ページより)
設計の現場で必ず役立つ!
有限要素法解析の様々な実践的ノウハウを理論と結びつけながら丁寧に解説.
適正なモデル化,要素の選定,メッシュ分割の工夫,境界条件の設定,材料物性の入力,解析結果の分析など実際に汎用コードを用いて計算する際に頻出する問題をピックアップし,実践ノウハウとしてまとめた.
東京大学の講義で長年使用された実践的な例題・演習を精選.それらはすべて無料で使えるソフトでシミュレーション演習が可能.専用のサポートサイトからダウンロードできる.






