ヘルムホルツの自由エネルギー

こんにちは、カヲルです！

今回は熱力学の一単元ですが、機械設計をやる上で参考になる概念と思われるヘルムホルツの自由エネルギーについて書きたいと思います。

熱力学第二法則

普段の生活の経験からも自然に起こる現象は一方通行のことが多い。

例えば、机に置いておいたホットコーヒーは時間が経てば冷めるが、何もせずに勝手に温まることはない。

また、綺麗に整列してあったものが時間が経つに従い乱雑になることはあるが、その逆もない。

エネルギーの保存則である熱力学第一法則だけでは説明できないものがここにある。

そこで熱力学ではエントロピー（Entropy）という状態量を導入する。

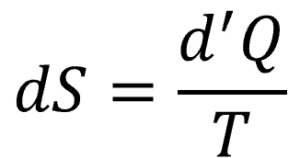
ここでSがエントロピー、Qが熱、Tが絶対温度である。なお、左辺と右辺が等号で結ばれているときは準静的な条件である。

エントロピーは「乱雑さ」と結びついてるが、この式はその原因が熱が熱であることを示してる。

以上を踏まえ、熱力学第二法則（エントロピー増大則）では断熱変化のときに下記であることが示されている。

上式で等号になる条件は準静的な条件であり、断熱変化ではエントロピーの変化dSは減少しないことを言っている。

ヘルムホルツの自由エネルギー

機械系で熱力学を勉強するとピストン・シリンダ系に代表される体積仕事が興味の中心にくることが多い。

ここで巨大な熱浴があり、等温変化する場合のみを考える。

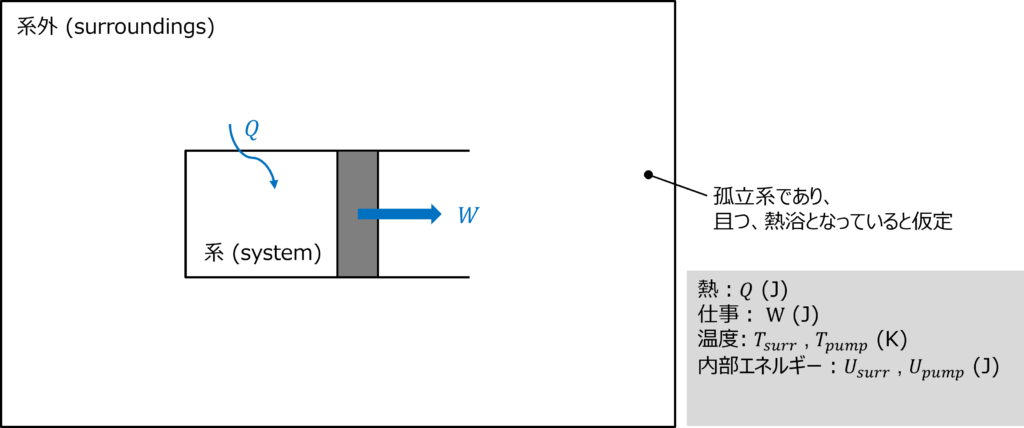
ここで系外のエントロピー変化をΔSsurr、系のエントロピー変化をΔSsysと置くと全系のエントロピー変化ΔStotは

となり、熱力学第一法則（エントロピー増大則）より

となる。エントロピーの定義より

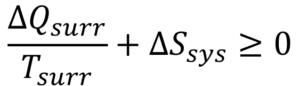
となる。ここで系は等温変化（Tsurr = Tsys)と仮定する。熱は系外から系への熱の移動となるため、

となる。熱力学第一法則（ΔU = Q + W）より

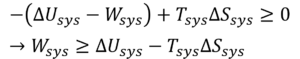
となる。

よって、

となる。