こんにちは、カヲルです!
今回は大学初学年で学習するテイラー級数とフーリエ級数について説明します。
社会に出てからも理工系の方は使用する数学ですので、是非イメージだけで掴んでもらえればと思います。
級数

級数とは
無限数列{an}の初項a1から順に各項をプラスで結んだ式を級数(series)または無限級数と言います。
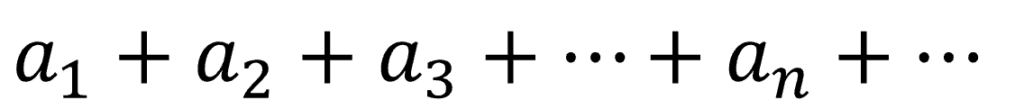
上式に総和記号(シグマ)を用いると下のように書くこともできます。
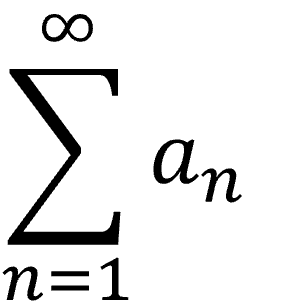

a1を初項、anを第n項と言うよ。
級数の例
級数の具体例としてはテイラー級数(Taylor series)、フーリエ級数(Fourier series)などがあります。
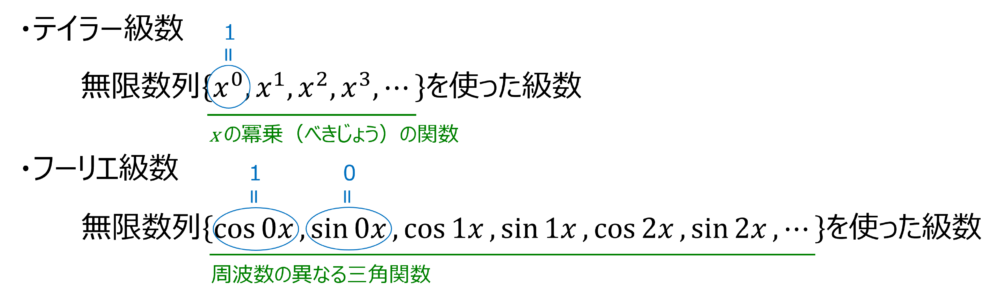

この2つは工学部での勉強を進める上でよく登場するよ。
テイラー展開

テイラー展開とは
無限回微分可能な関数f(x)は冪乗(べきじょう)の関数の和で展開できる場合があります。
この冪乗級数に展開することをテイラー展開(Taylor expansion)と言います。
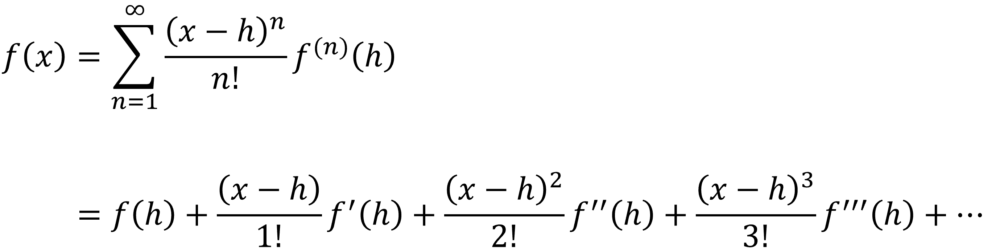
ここで関数f(x)の原点まわり(h=0)での展開の場合を特別にマクローリン展開(Maclaurin expansion)と言います。
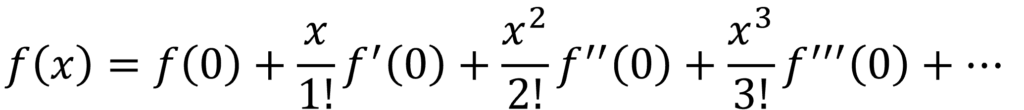

マクローリン展開はテイラー展開の一種だよ!
テイラー展開のイメージ
イメージを掴むために例としてf(x)= sin xの原点まわりのテイラー展開(マクローリン展開)を行いましょう。
まず、各項ごとに計算すると
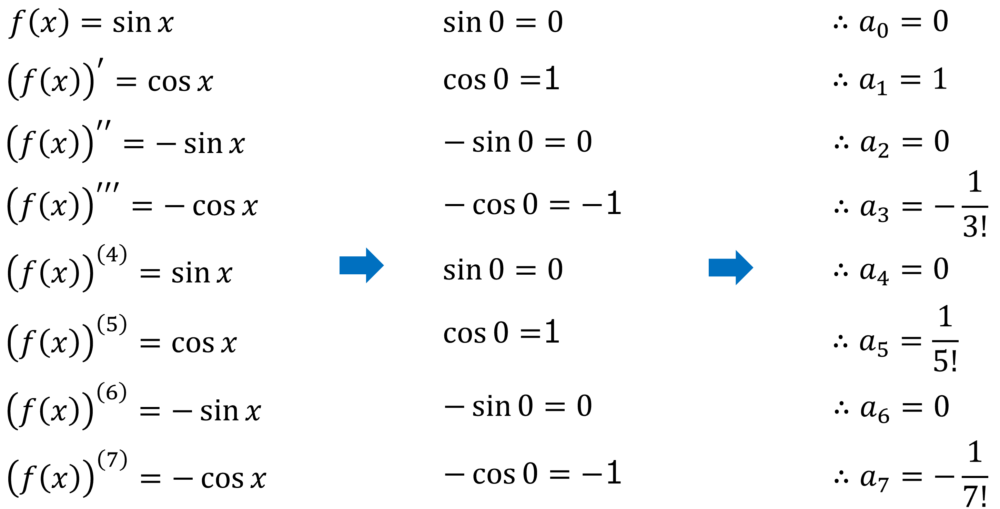
となり、f(x) =sin x のマクローリン展開は
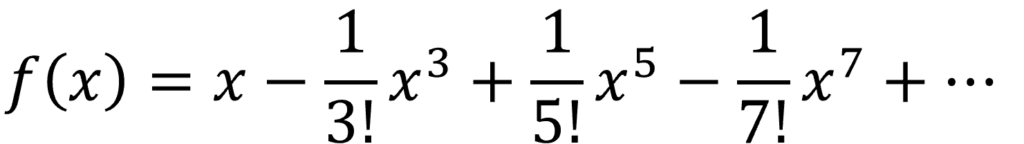
となります。これを用いてグラフ化してみます。
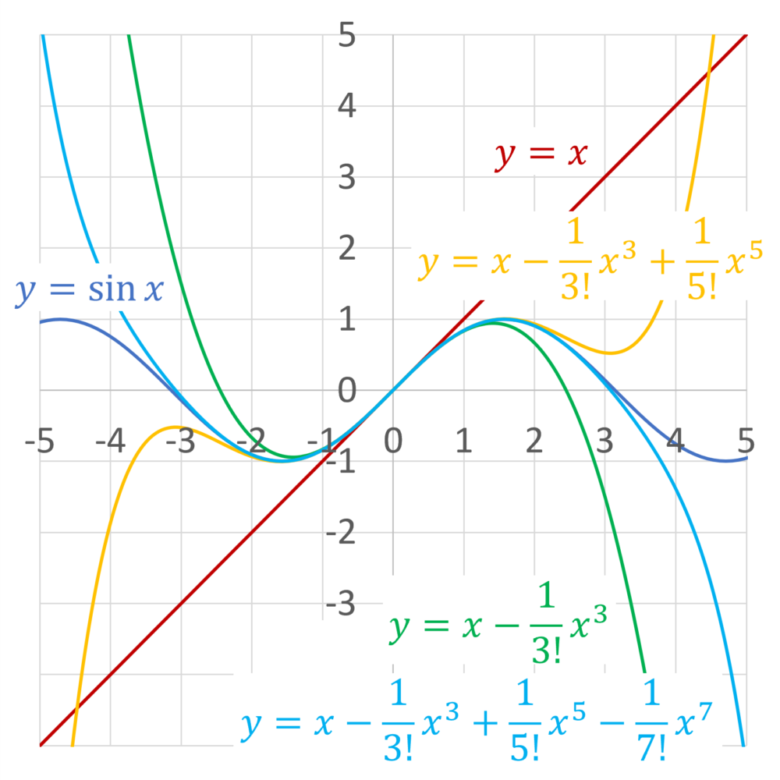
次数が上がるほど、元の関数y = sin x に近くなることがグラフからも分かります。

高校で習う近似式 sin x ≈ x (|x| ≪ 1) はテイラー展開からきているよ。
フーリエ級数展開
周期関数とは
テイラー級数は周期をもっていませんが、物理学や工学で現れる現象には周期現象が非常に多くあります。(Ex. 音、機械的振動、電波など)
ここで、与えられた関数f(x) が下式を満足するとき周期2π の周期関数(periodic function)であると言います。
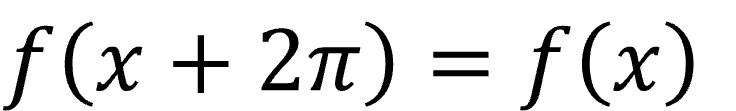
フーリエ級数展開とは
関数f(x) が周期関数であれば下のような三角級数に展開できる場合があります。
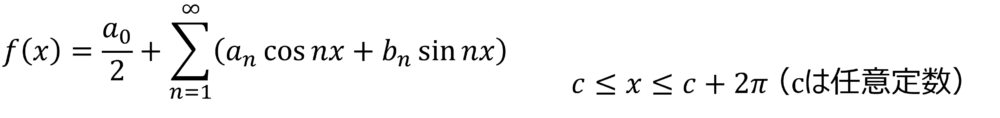
上式をf(x) のフーリエ級数展開と言い、an, bn をフーリエ係数と言います。
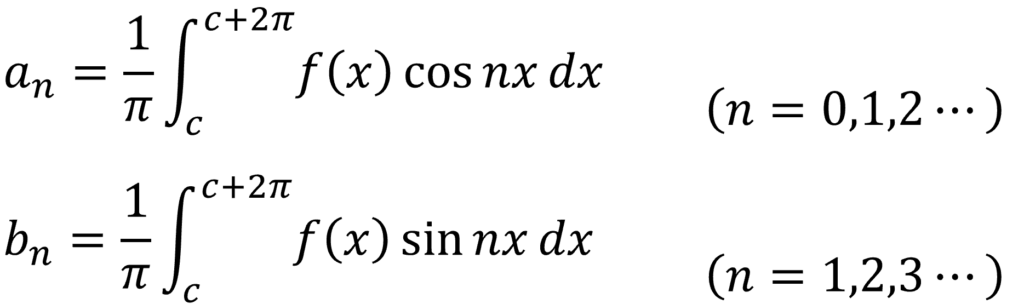
フーリエ級数展開のイメージ
イメージを掴むために例としてf(x) = xを区間 -π ≤ x ≤ π でフーリエ級数に展開してみましょう。
まず、フーリエ係数anを求めます。
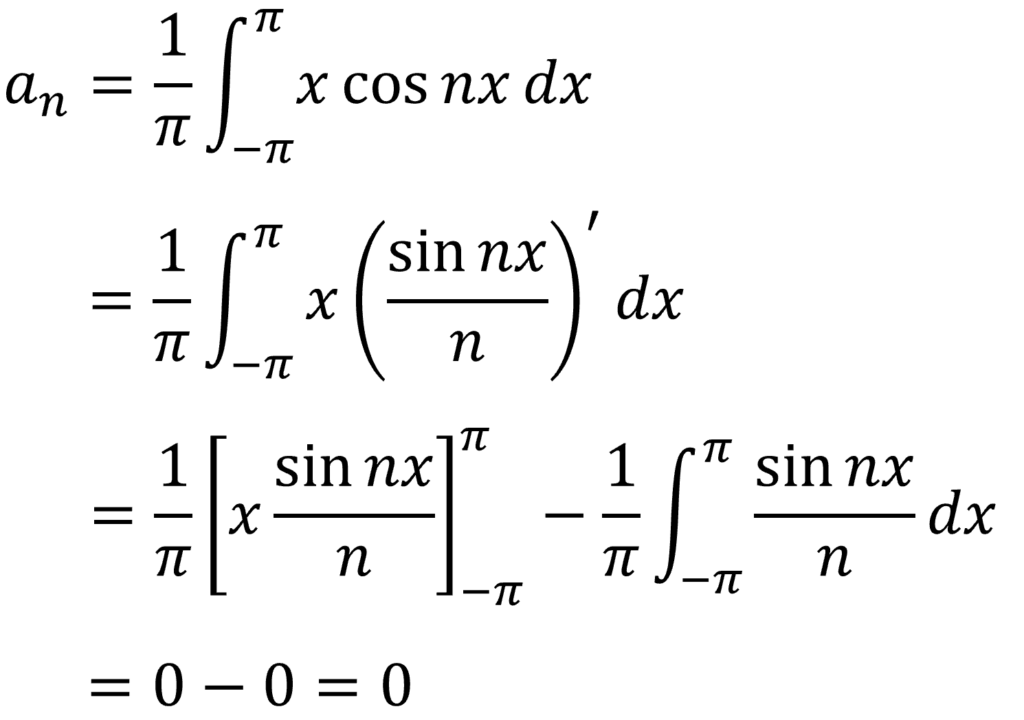

f(x)が奇関数の場合はanはすべてゼロになるよ。
つぎにフーリエ係数bn を求めます。
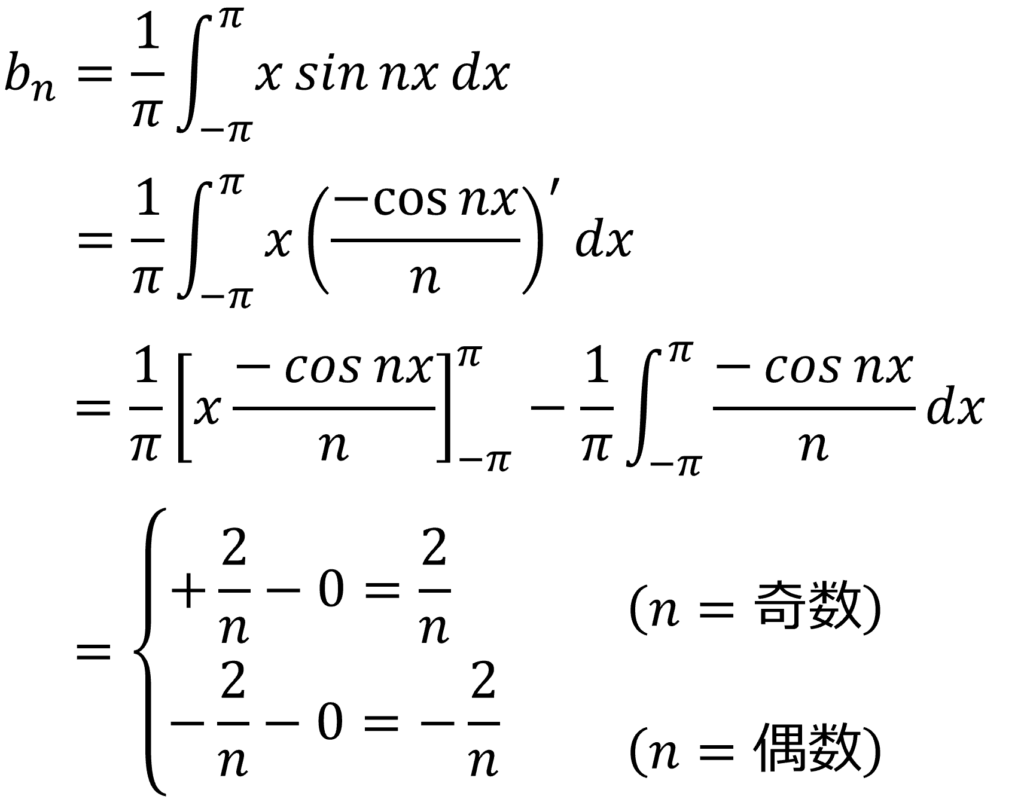
よって、 f(x)=x のフーリエ級数展開は
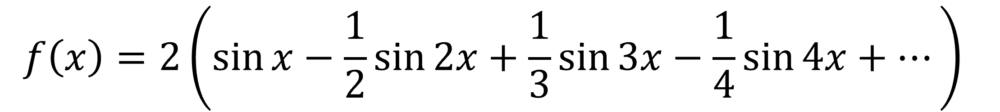
となります。これを用いてグラフ化してみます。
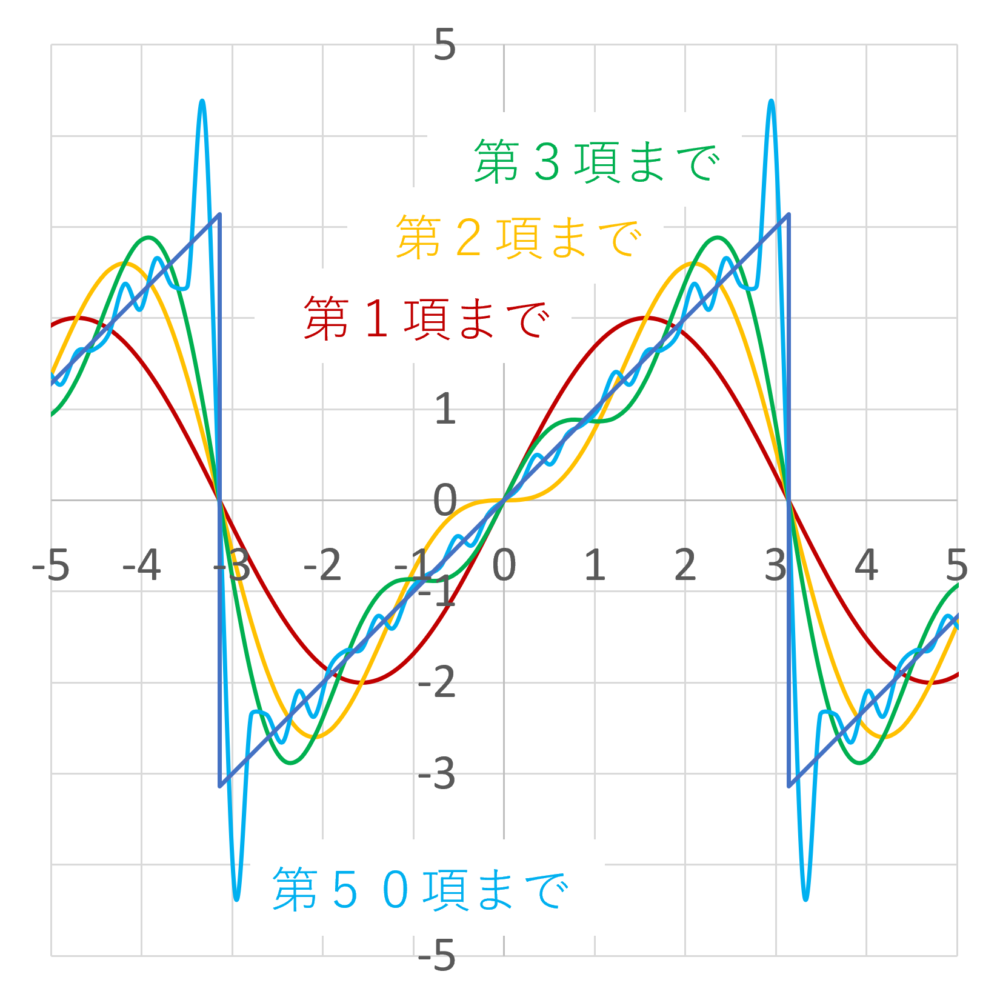
項数が多くなるほど、元の関数y = x (のこぎり波)に近づくことがグラフからも分かります。
フーリエ級数の微分
一般に微分と極限の交換はできませんが、もし、交換が可能であれば代数的操作のみで簡単に微分が行えます。
このようなとき、項別微分可能定理が使えれば簡単に微分可能になります。

2π を周期とする関数f(x) が連続で、f’(x) も連続で区分的に滑らかならば、f(x) は項別微分可能であり、f’(x) のフーリエ級数は
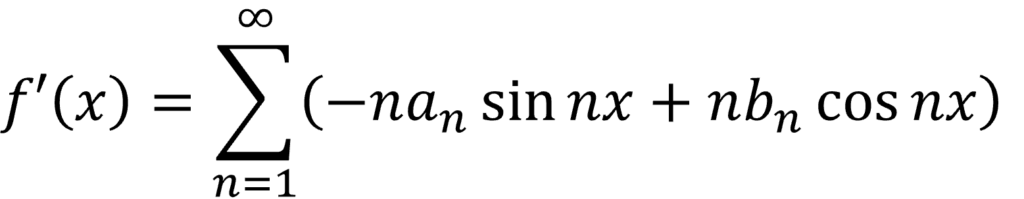
で得られます。

区分的に滑らか
関数f(x) が連続で、f’(x) が区分的に連続であれば、関数f(x) を「区分的に滑らか」と言うよ。
フーリエ級数の積分
同様に項別積分可能定理が使えれば簡単に積分可能になります。
関数f(x) が[-π, π]で区分的に連続ならば、任意のx ∈ [-π, π]に対して
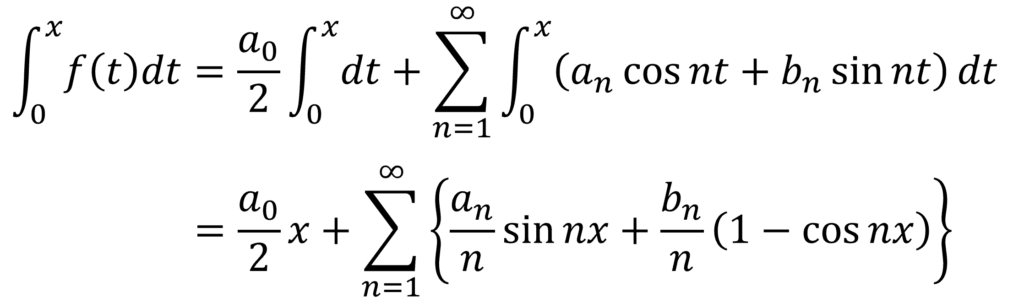
が成り立ちます。



