任意の曲面同士の接触面圧計算【ヘルツの接触理論】

円柱同士や球同士の接触などについては以下の記事で接触面圧の計算方法を解説しました。

しかし、$x$方向、$y$方向で曲率の異なる任意の曲面同士では計算出来ませんでした。

ヘルツの接触理論（Hertz contact theory）を用いて、今回は任意の曲面での接触面圧を求める方法について解説します。

2022年1月5日線接触・面接触の接触面圧を求めよう！【ヘルツの接触理論】

任意の曲面同士の接触面圧

Fig. 1に示す通り、弾性体１と弾性体２が荷重$W$を受けて接触しているとき、接触による圧力分布はヘルツの接触理論によって求めることができます。

しかし、任意の曲面同士の接触の場合は解析的に求めることが難しくコンピュータによる数値計算が必要になります。本記事では扱いが容易なBrewとHamrockによる近似式を紹介します。

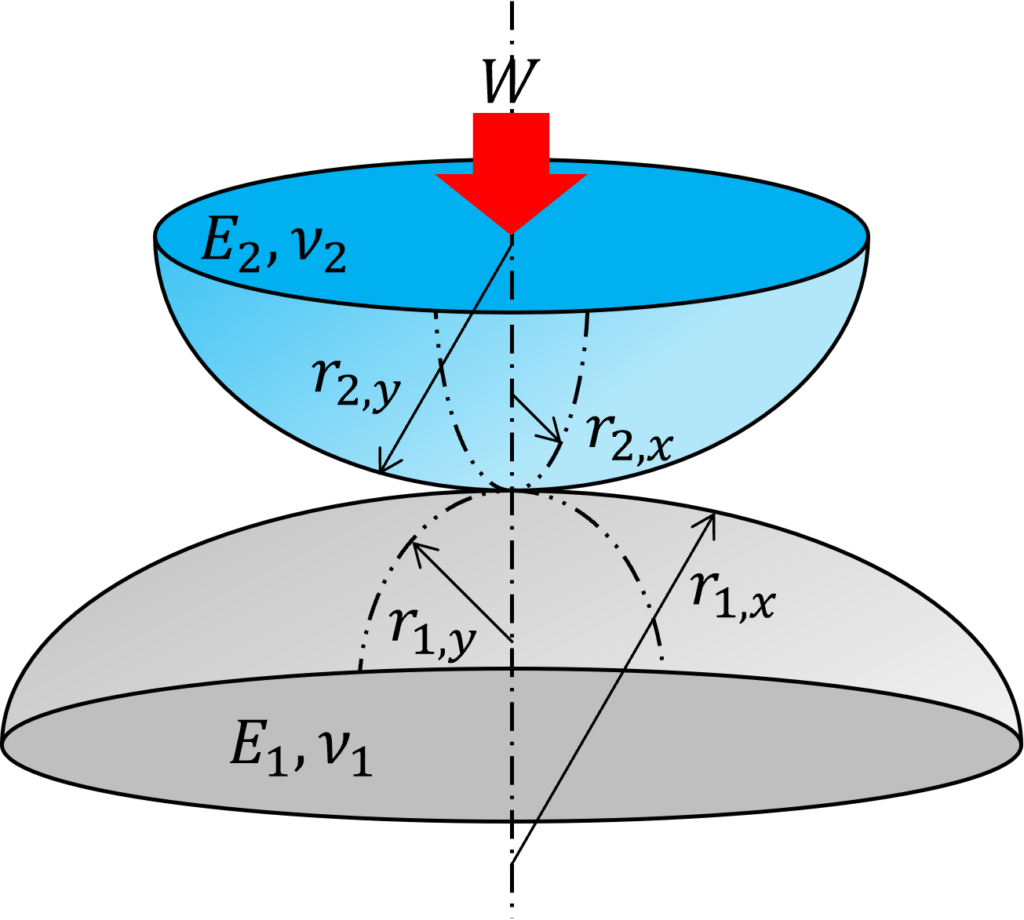
弾性体１と弾性体２の曲率半径をそれぞれ$R_1$、$R_2$とおき、$x$方向と$y$方向の座標軸を$1/R_x > 1/R_y$となるように設定します。

$$\begin{eqnarray} \frac{1}{R} &=& \frac{1}{R_x} + \frac{1}{R_y} \tag{1}\\ \\ R_x &=& \frac{R_{1,x} \cdot R_{2,x}}{R_{1,x}+R_{2,x}} \tag{2}\\ R_y &=& \frac{R_{1,y} \cdot R_{2,y}}{R_{1,y}+R_{2,y}} \tag{3} \end{eqnarray}$$

つぎに、球同士や円柱同士の接触と同様に等価ヤング率$E’$を求めます。

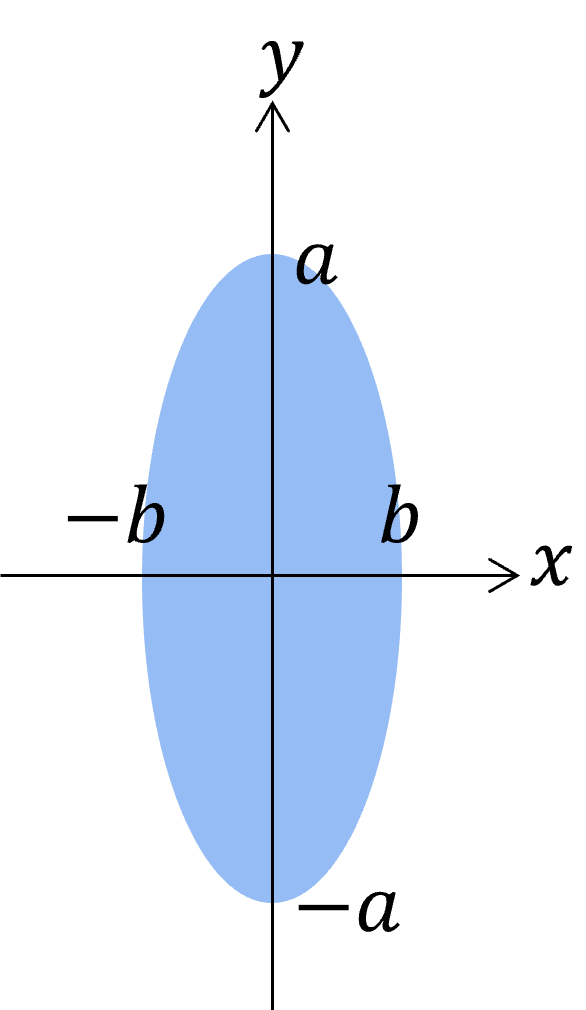
$$ \frac{1}{E’} = \frac{1}{2} \left( \frac{1 – \nu_1^2}{E_1} + \frac{1 – \nu_2^2}{E_2} \right) \tag{4} $$

ここで、Fig. 2に示すような$x$方向と$y$方向の接触半幅$a$、$b$を求めます。

接触半幅は上記で求めた等価曲率半径$R$と等価ヤング率$E’$を用い、下式で求められます。

$$\begin{eqnarray} a &=& \left( \frac{6 k^2 \varepsilon W R}{\pi E’} \right)^{\frac{1}{3}} \tag{5}\\ b &=& \left( \frac{6 \varepsilon W R}{\pi k E’} \right)^{\frac{1}{3}} \tag{6} \end{eqnarray}$$

また、式（５）、（６）の$k$と$\varepsilon$は下式で与えられます。

$$\begin{eqnarray} k &=& 1.0339 \left( \frac{R_y}{R_x} \right)^{0.636} \tag{7}\\ \varepsilon &=& 1.0003 + 0.5968 \left( \frac{R_x}{R_y} \right) \tag{8} \end{eqnarray}$$

以上を用いて、平均接触面圧$P_{mean}$（平均ヘルツ面圧）は下式にて求められます。

$$ P_{mean} = \frac{W}{\pi a b} \tag{9} $$

最大接触面圧$P_{max}$（最大ヘルツ圧）は、球同士や円柱同士の接触と同様に下式の関係となります。

$$ P_{max} = 1.5 \, P_{mean} \tag{10} $$

なお、下式を用いると任意の位置(x, y)における接触面圧$P$を求めることが出来ます。

$$ P = P_{max} \sqrt{1- \left( \frac{x}{b} \right)^2 – \left( \frac{y}{a} \right)^2} \tag{11} $$

まとめ

本記事では任意の曲面での接触面圧を求める方法について解説しました。

接触面圧が知りたいときは摩擦・摩耗で課題を抱えている場合も多いかと思います。これを機会に摩擦・摩耗を扱うトライボロジーを勉強してみては如何でしょうか。

「図解トライボロジー」はタイトルの通り、図も多く初学者にも配慮された読みやすい構成となっています。また、演習問題も解説も式の省略も少なく理解しやすくなっています。

リンク

　
オーム社の「トライボロジー」は上で紹介した本が物足りなくなった場合に読むことをおすすめします。数式は少し増えますが、基本に忠実に学びたいかたはこちらの本がよいかと思います。

リンク

2022年10月30日摩擦面の温度の計算方法【閃光温度】

2022年11月29日潤滑油（オイル）の粘度と温度の関係式

2022年11月27日圧入荷重・スリップトルクの計算法と式の導出

【付録】物性表

参考までに各工業材料の物性表を記載します。

材料名	ヤング率 (GPa)	ポアソン比 –	線膨張係数 (×10^-6/K)	比重 –
SUJ2	207	0.30	12.5	7.83
SPCC	211	0.30	11.7	7.86
S25C	206	0.28	11.8	7.84
S45C	207	0.30	12.8	7.83
SUS303	193	0.29	17.3	8.03
SUS304	193	0.29	16.3	7.93
SUS420J2	200	0.27	10.4	7.75
SUS430	200	0.27	10.4	7.70
A2017	73	0.33	23.6	2.79
A5056	72	0.30	24.3	2.64
ADC12	71	0.28	21.0	2.73
ADC14	81	0.28	19.0	2.70
C2600	110	0.33	19.9	8.53
C3604	96	0.32	20.5	8.50
POM	3.4	0.35	–	1.42
PA6-GF30	7.3	0.35	–	1.36
PA66-GF30	8.0	0.35	–	1.36
PBT-GF30	9.5	0.38	–	1.53
PPS-GF40	13.0	0.37	–	1.66