自動車業界を中心にフロントローディングによる開発効率向上のため、モデルベース開発(MBD)が盛んに行われ始めてしばらく経ちますが、1Dモデルが巨大化していくにつれ、処理の遅さが問題となる場合があります。
また、現在はソフトウェアが産業の中で重要な地位を占めており、プログラムを高速に実行したいと考えることもあるかと思います。
行列を用いて方程式を解いている場合、もしゼロの塊(ブロック)があるときはその部分を区分け(分割)し、計算を簡略化することで処理スピードの高速化を狙える場合もあります。
本記事では、区分行列の和と積の計算方法ついて説明します。
区分行列とは
区分行列は大きな行列を計算しやすいように、小さな行列に区分けして計算することを目的の一つとしています。
しかし、区分けの仕方はデタラメに決めて良い訳ではなく、線形代数の計算のルールに則って区分けする必要があります。
行列の和 \(A + B\)
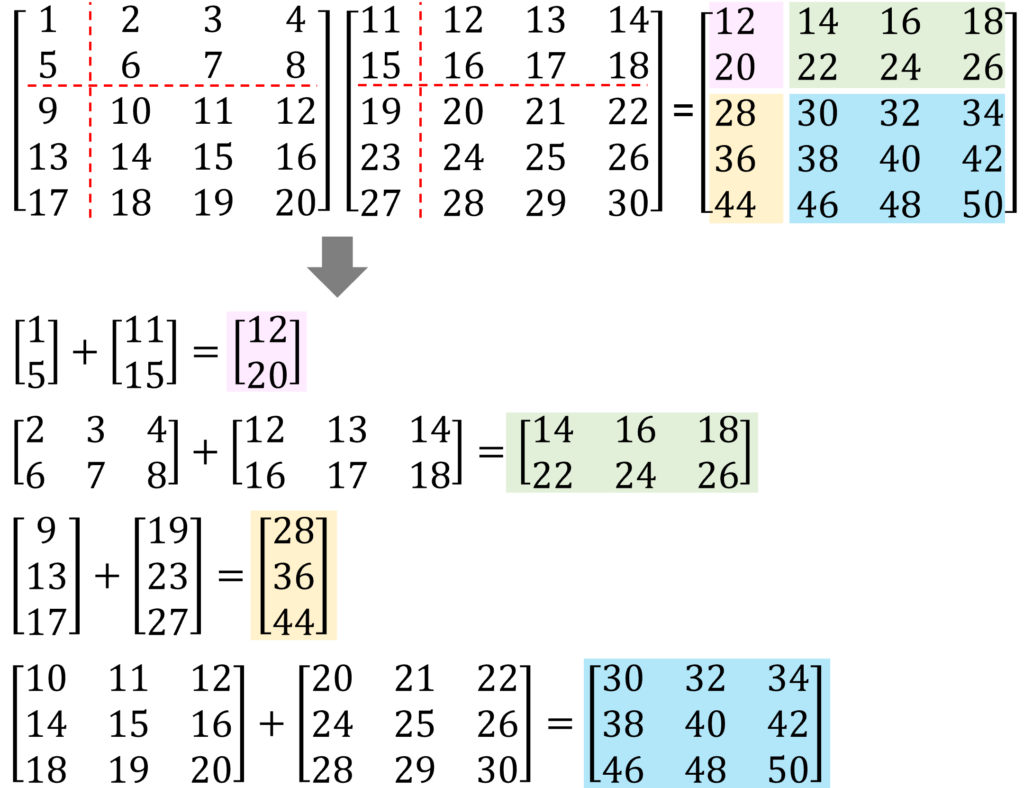
行列\(A\)と行列\(B\)の和(足し算)は、以下のルールで区分けしなければいけません。
- 行列\(A\)と行列\(B\)は全く同じように区分けをする
以下に例題を示します。
行列の積 \(A \, B\)
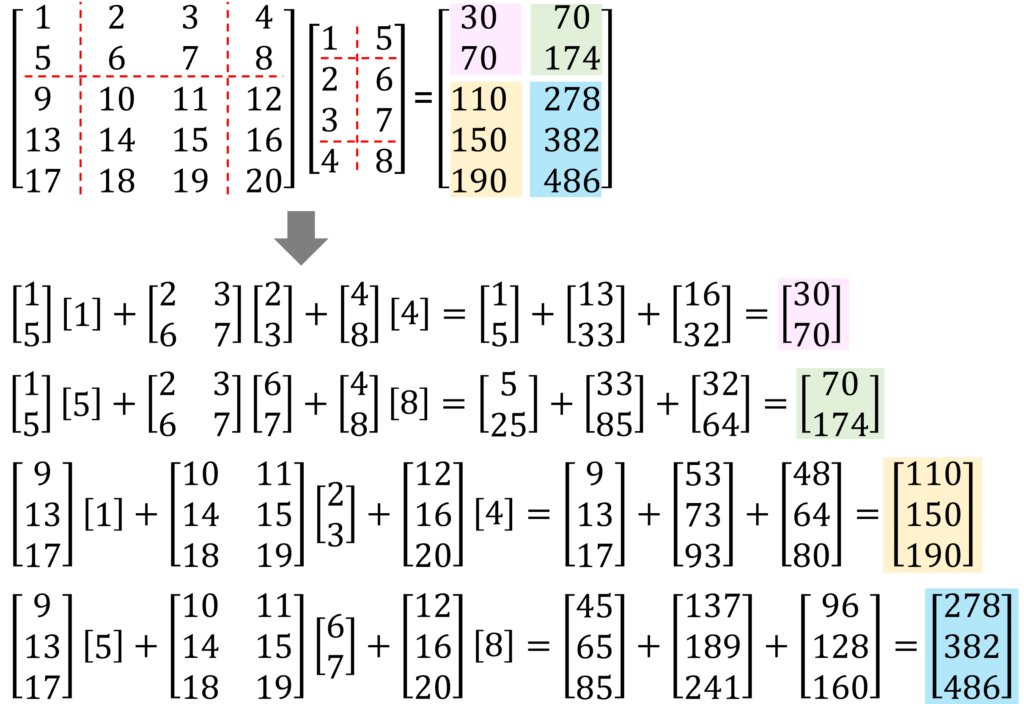
行列\(A\)と行列\(B\)の積(掛け算)は、以下のルールで区分けしなければいけません。
- 行列\(A\)と行列\(B\)の積(掛け算)を行う場合、行列\(A\)の横方向の区分けの数と行数\(B\)の縦方向の区分けの数を一致させる。
- 行列\(A\)の横方向の区分けの仕方と行数\(B\)の縦方向の区分けの仕方を一致させる。
(前の区分けの列数と後ろの区分けの行数が一致)
以下に例題を示します。
行列の区分けに関しては古賀 真輝さんの動画が分かりやすいよ!
まとめ
今回は線形代数学で習う区分行列について見ていきました。
コンピュータに実装する方法はいろいろありますが、行列の計算はMATLABが非常に便利です。
下記の記事ではMATLAB/Simlinkのブロック上で行列を扱う方法を紹介していますので、参考までに見て頂ければと思います。
また、以下の記事ではMATLAB/Simlinkのブロック上で行列の連結と分割方法も紹介していますので、併せて見て頂ければ思います。
もし、MATLAB自体をしっかり勉強されたい方は、以下のハンドブックが羅列的に見やすくまとめられておりおすすめです。





