気体の内部流れについて着目するとき、流路があるところで狭くなったり、広くなったりする部分の解析(計算)を行いたい場合があります。
流路があるところで狭くなる流れ(流路急縮小)に関しては、穴の開いたタンクから流出する流れと考えることができ、以前の記事で紹介したオリフィスの式を適用できます。
一方、流路があるところで広くなる流れ(流路急拡大)に関しては、流れの後方で大きな渦(剥離)が出来るなど、流れの様相としては複雑で式化が難しい現象です。
本記事では、前後の圧力差によって気体が流れる流路急拡大部の流れの取り扱い方法について紹介します。
流路急拡大
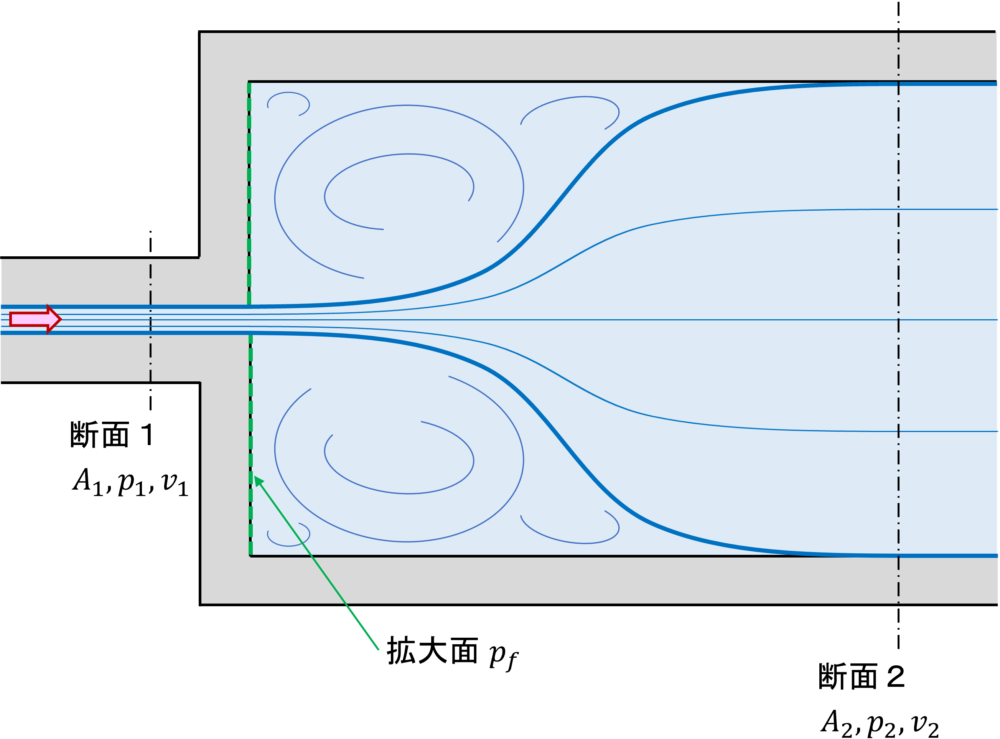
下図のように断面積\(A_1\,(m)\)の流路から、これよりも大きな断面積\(A_2\,(m)\)への流れについて考えます。
このとき、流れは断面1(圧力\(p_1\,(Pa\:abs.)\), 流速\(v_1\,(m/s)\))で一様で、急拡大部を通って減速し、断面2(圧力\(p_2\,(Pa\:abs.)\), 流速\(v_2\,(m/s)\))で再付着して一様になるものとします。
また、拡大面の圧力を\(p_f\,(Pa\:abs.)\)とします。
ここで、流れを整理するために音速\(a\)と流速\(v\)との比であるマッハ数\(M\)を導入します。
fig. 1の流れは定常流であるとして質量流量を\(\dot{m}\,(kg/s)\)、比熱比(空気の場合は1.4)を\(\kappa\)、断面1での音速を\(a_1\,(m/s)\)、密度を\(\rho_1\,(kg/m^3)\)、断面2での音速を\(a_2\,(m/s)\)、密度を\(\rho_2\,(kg/m^3)\)と置くと、それぞれの断面でのマッハ数\(M_1,\,M_2\)は以下のようになります。

もし、密度\(\rho\)が分からない場合は温度\(T\,(K)\)が分かれば、理想気体の状態方程式より求めることができますね。
\(\rho=\displaystyle\frac{p}{R\,T} \tag{3}\)
気体定数\(R\)は前の記事で求めた通り、空気の場合は約\(287 \, J/(kg\cdot K)\)となりますね。
流路急拡大部において、式(1)、(2)で求めたマッハ数同士の関係は以下のようになります。
※ 拡大面積比 \(\phi \equiv \frac{A_1}{A_2}\)
式(4)は下図のようなバックステップ流れにも適用できるよ!

ここで、式(4)について見てみると、\(M_1\)、\(\phi\)および\(p_f/p_1\)が分かれば、数値計算等を行うことにより\(M_2\)を求めることができます。
\(p_f\)に関して見てみると、\(A_1\)に対して\(A_2\)のほうが遥かに大きく、\(M_1\)が十分小さければ\(p_2\)とほぼ同等となり、\(p_f/p_1 \approx p_2/p_1\)とすることができます。
もし、\(M_1\)が大きな領域まで拡張したい場合は、実験や流体解析ソフト等で求めた結果をもとに、\(M_1\)と\(p_f/p_1\)との関係を整理して再計算することとなります。
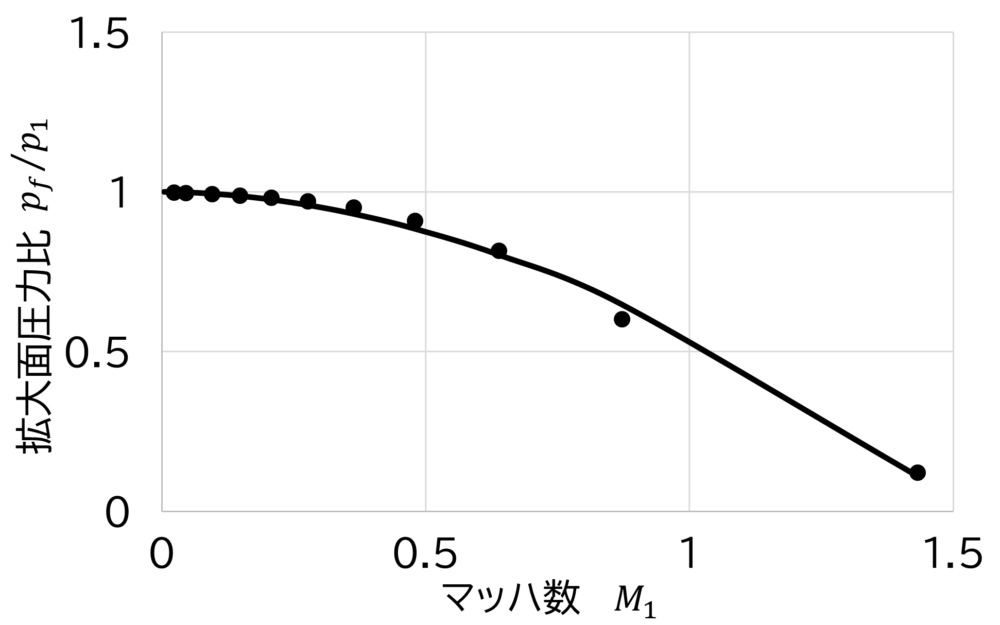
fig. 3のグラフは拡大面積比\(\phi\)ごとに異なるので、個別に整理してみてね!

森棟氏らの「管路系の高速流動特性に関する研究 : 第2報,急拡大を伴う場合」という論文が参考になりますね。



