MATLABによる非線形方程式の解法【第１回】

製品開発手法として、コンピュータ上で実際の製品と同様なふるまうをするモデルを作成して設計を行うモデルベース開発（MBD）というものがあります。

物理や化学などの基本法則（支配方程式）やそれらの解析解を用いてモデルを作成していきますが、その中には非線形方程式が度々登場します。

これらは数式変形では解くことが難しい（解析的に解けない）ことが多く、コンピュータを使った繰り返し計算（数値計算）を行って解くことがほとんどです。

本記事では、非線形方程式をニュートン・ラフソン法を用いてMATLABで解く方法を解説します。

カヲル

有料の「Optimization Toolbox」をインストールし、fsolve関数を用いるとMATLABで非線形方程式を解けるけど、本記事はそれを使わない方法を解説するね！

理論編

本記事は「理論編」とMATLABによる「実践編」の二部構成としています。あまりご興味のない方は先に読み飛ばしてもらてっても構いません。

ニュートン・ラフソン法とは

非線形方程式を適切に移項し右辺がゼロの形、つまり$f(x) = 0$とし、その方程式の近似値を$x_0$とします。
このとき、$f(x)$を$x = x_0$周りでテイラー展開すると以下のようになります。

$$ f(x) = f(x_0) + \frac{1}{1!}f'(x_0)(x-x_0)+\frac{1}{2!}f\,”(x_0)(x-x_0)^2+\cdots=0 \tag{1} $$

ここで、２次以降を省略して式変形すると以下のようになります。

$$ \begin{eqnarray} &&f(x_0) + f'(x_0)(x-x_0) \approx 0 \tag{2}\\ \\ &&\to f'(x_0)(x-x_0) = \,-\ f(x_0) \tag{3}\\ \\ &&\to x = x_0 \,-\, \frac{f(x_0)}{f'(x_0)} \tag{4} \end{eqnarray} $$

式（４）より漸化式にすると下式のようになります。
下式より近似値$x_0$から次の計算ステップの推定値を求めていくことが出来ます。

$$ x_{k+1} = x_{k} \,-\, \frac{f(x_k)}{f'(x_k)} \tag{5} $$

これを繰り返して解を求める方法をニュートン・ラフソン法（Newton-Raphson method）と言います。

ニュートン・ラフソン法による非線形方程式の数値計算（数値解析）の手順を以下に示します。

数値計算の手順

ステップ１

非線形方程式$f(x)$の解の近似値$x_0$を推定し、これを初期値$x_k$とする。

ステップ２

下式より、より真値に近い近似値を計算する。

$$ x_{k+1} = x_{k} \,-\, \frac{f(x_k)}{f'(x_k)} \tag{5} $$

ステップ３

ステップ２を$k = 1, \,2,\,3,\, \cdots$とし、繰り返し計算する。
次の収束条件を満たしたとき、繰り返し計算を止める。

$$ |f(x_{k+1})| \lt \delta \tag{6} $$

　
これは、解くべき方程式を$f(x)=0$としたので、繰り返し計算を行うとゼロに段々近くなり、$f(x)$の値を都度確認することで収束の判断が出来るからである。つまり、$\delta$はゼロに近い「小さな正数」を指定する。

実際に入力する数値は必要な計算精度に合わせて設定します。

カヲル

もし、上記の手順で$f'(x_k)$がゼロ又は異常に小さな値になると計算が続けられなくなるよ。

【関連記事】テイラー展開とは

テイラー展開についてもう少し知りたい方は以下の記事を参考にしてみてください。

2022年7月14日テイラー級数・フーリエ級数のイメージを掴もう！

ニュートン・ラフソン法の図形的意味

中学２年生で学習した通り、点$(a,\,b)$を通る傾き$m$の直線の方程式は$y-b=m(x-a)$でした。また、ある関数$f(x)$の$x$における接線の傾きはその関数を微分した$f'(x)$であることは数Ⅱで学習しました。

このことから、式（５）で与えらえる$x_{k+1}$は点$x_k$での$f(x)$での接線と$x$軸との交点座標となることが分かるかと思います。

$$ y \,- f(x_k)= f'(x_k)(x-x_k) \tag{7} $$

これをグラフで表すと下図のようになります。
このグラフを見てわかる通り、重解になっている場合は初期の近似値$x_0$により求まる解も異なります。

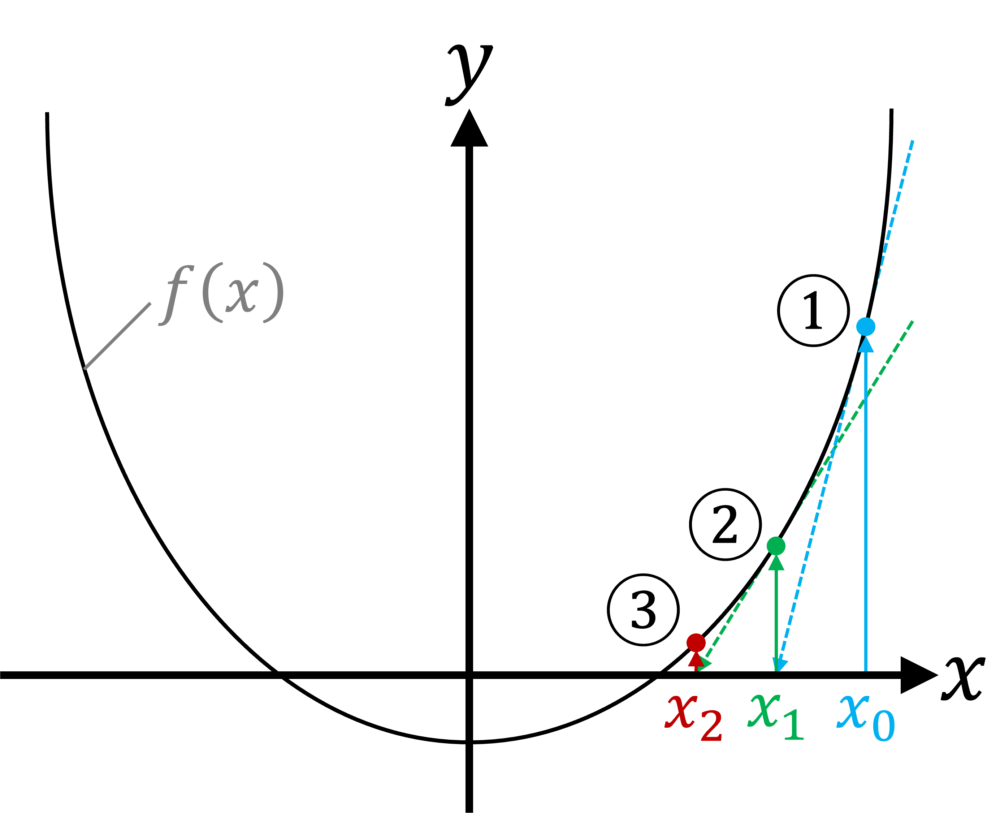
また、$f'(x) = 0$となると繰り返し計算が続けられなくなる理由もグラフを見れば納得いくかと思います。このことから、ニュートン・ラフソン法は初期の近似値を適切にとることがなにより重要であることが分かります。

カヲル

例えば、$sin(x)$のような周期関数では、$y = 0$との交点が無数にあるので初期の近似値$x_0$を適切に設定しないと欲しい値が求められないよ！

実践編

では、実践編としてニュートン・ラフソン法で方程式を解いてみましょう。

ここでは、MATLABを用いてコンピュータで解きますが、答え合わせもしたいので簡単に解ける以下の方程式を例題にします。

例題

ニュートン・ラフソン法を用いて、$x$について求めよ。なお、初期の近似値$x_0$は1とし、相対誤差$\delta$は$10^{-9}$とせよ。

$$ x^2 = 3 \tag{8} $$

まず、式（８）を以下のように$f(x)=0$の形にします。

$$ f(x) = x^2 – 3 \quad(= 0)\tag{9} $$

つぎに式（９）を一階微分します。

$$ f'(x) = 2x \tag{10} $$

式（９）と（１０）を用いて、理論編に記載した「数値計算の手順」をもとにMATLABで実装します。なお、収束しない場合の無限ループを避けるためにfor文を用います。

clc; clear;
x = 1;                  % 初期の近似値を設定

for i = 1:1:100         % 最大反復数を制限   
    fx   = x^2 - 3;
    if abs(fx) < 10^-9  % 収束判定
        break;
    end
    
    dfdx = 2*x;
    x    = x - fx/dfdx; % 近似値計算
end

format long;            % 出力桁数設定
disp(x);                % 出力

上記をMATLABで実行すると「1.732050807568877」と表示されます。

この方程式の答えは$x = \sqrt{3}\ = 1.7320508\cdots$ですので、正しく計算できていることが分かります。