こんにちは、カヲルです!
今回は大学で習う線積分に関して初学者に分かりやすく、イメージを掴んでもらうことを目的に書きたいと思います。
線積分
高校で習う積分は直線(x軸)と曲線f(x)との間のの平面状の面積を求める計算でした。
線積分では直線(x軸)に固定せずに下図のように平面xy上に曲線Cがあるものとします。そして、この曲線C は(x (t), y (t))のようにパラメータ表示できるものとします。
ここで、位置を指定すると高さを返す関数z があるものとします。
線積分(line-integral)で計算するのは下図のカーテン状の領域の面積になります。
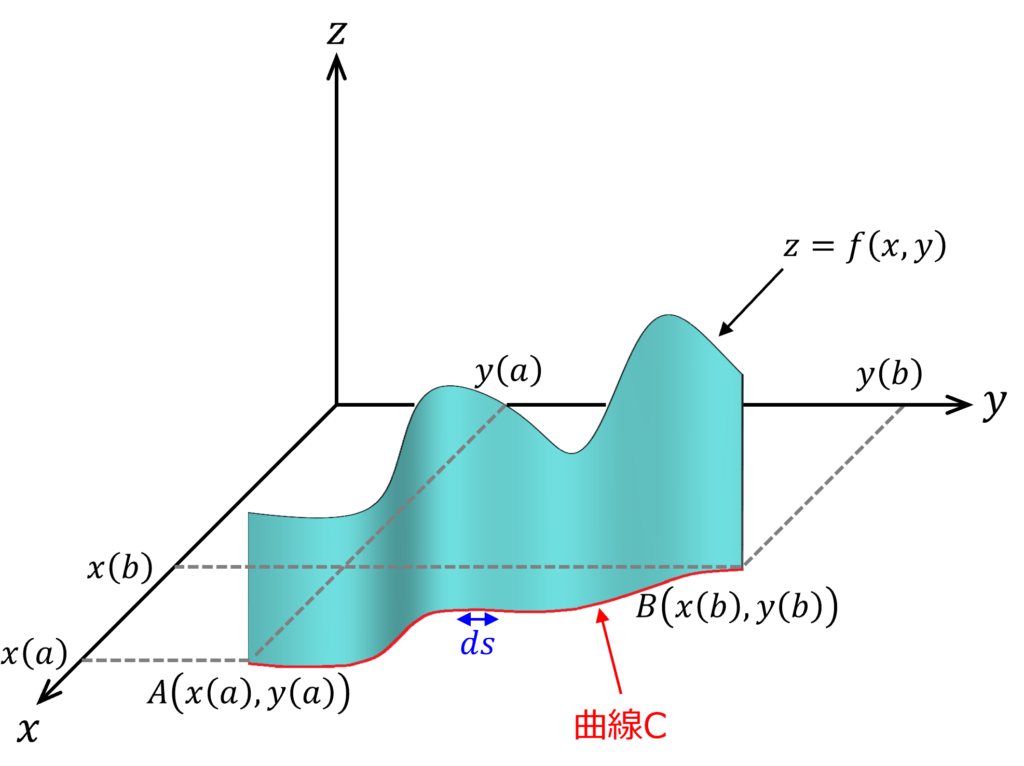
曲線C を積分路(contour)或いは積分の道(path of integration)と言うよ。
![]()
線積分の計算
関数z =f (x, y ) を曲線C で線積分すると下式になります。
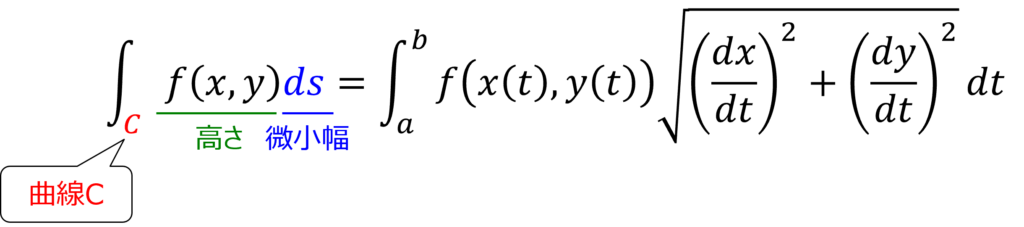
上の式は曲線C は微小幅で見ると直線に近似できるため、三平方の定理で長さ(幅)を計算できることを利用しているよ。
![]()
ここでf (x, y ) = 1 の場合は下式となり、曲線C の長さとなります。
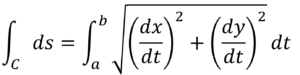
上のグラフは開曲線を示していますが、閉曲線の線積分を特に周回積分と言い、専用の積分記号∲ を用いることもあります。
リンク
リンク



