こんにちは、カヲルです!
皆さんは温度を測定したことはありますでしょうか。したことない人はいませんよね (^^;
理科の実験で気温の測定やアルコールランプなどで熱した液体の温度を測定したり、風邪を引いた時に体温を測定したり、温度測定は身近なものですよね。
今回は途中までの温度測定結果しかないものに対して物体の温度を予測したり、条件(熱の流入量や流出量)が変わった場合の予測について取り上げたいと思います。過去の実験データを用いて機械や電子機器の温度を予測できると便利かと思います。
この記事では実験データの整理の仕方とMicrosoft Excelを使って予測する方法を書きたいと思います。実験主体の内容となっており、熱流体解析ソフトを使って計算するようなことはしませんのでご了承願います。
なお、今回は少し長くなりますので回を分けて書きたいと思います。
【補足】熱流体解析ソフト
熱流体解析とは液体や気体などの流体の流れや熱の移動といった物理現象を流体力学を応用して解析することを言います。熱流体解析ソフトは流体力学の支配方程式(基礎方程式)であるナビエストークス方程式(2階非線形偏微分方程式)を離散化し、コンピュータで解くためのソフトとなります。英語で Computational fluid dynamics(CFD)とも言われます。
流速、圧力、温度の分布などをコンピュータ上で確認し、最適な設計をするために自動車、航空機、電子機器などあらゆるものの設計に使われています。
まずは温度予測の身近な例から見ていきたいと思います。
温度予測の身近な例
温度予測の身近な例としては右図のような予測検温機能が付いた体温計があるかと思います。
通常、体温計は室内に置かれるので温度センサー(サーミスタ)は室温になっています。体温を測定しようと脇下(又は口腔内)に入れると人体から熱が伝わり、体温計の温度センサーは温められますがすぐに体温と同じ温度になる訳ではありません。
通常は脇をしっかり閉じて10分程度経過させないと体温と温度センサーが同じ温度にならないため、正確な値が読み取れません。(短い測定時間だと温度センサーが体温で温まりきらず、低い温度が表示されてしまいます。)
詳しい仕組みは公表されていないようですが、上記のような温度センサーの熱応答を考慮して短い時間(近年の体温計だと数秒から数十秒)で体温が分かるように体温計内部で適切に演算し、我々に教えてくれる仕組みになっています。
(人体の温度は比較的高温で且つ恒温な「中核部(core)」と比較的低温で環境などで変動がしやすい「外殻層(chell)」があり、実際に生命活動が行われている内核部の温度を体温とするのが好ましいとされています。体温は脇を閉じて外気と遮断された空間ができ、その空間が内核部の温度に近づいてから測定する必要があります。その内核部の温度が近づくための時間も実際には必要であり、各メーカーの体温計は補正がなされていると推測されますが、ここでは省略させてください。)
温度変化の計算式
では本題に入りたいと思います。上記で人体から熱が温度センサーに伝わってもすぐには体温と同じにならないことを述べました。このことを数式で合わし極簡単な数理モデルに直していきたいと思います。
【補足】数理モデル
数理モデルとは現実世界で起こるさまざまな現象(物理現象、社会現象など)をよく観察し、数学の言葉(≒ 数式)で書き記したものを言います。日本語や英語などの自然言語で書いたものと比べ、端的かつ正確に書き記すことができます。また、数式にすることでその現象の性質の理解に役立てたり、更に現象を理解をするために追加の実験・観察を行ったりすることを繰り返すことで深い理解ができるようになります。また、数理モデルを作ることでその現象に変化があるときに、どのように応答をするかを予測することもできます。
さて、温度センサーがすぐに体温と同じ温度にならないのは物体には固有の温まりにくさというものがあるからです。これを熱容量と言い、単位は J/K(ジュール・パー・ケルビン)となります。熱容量は物体の温度を1K(1℃)上げるのに必要な熱量となります。
身近な温度予測の例として体温計を挙げましたが、以降ではよりシンプルで分かりやすいモデルとしてビーカーに入っている液体をヒータで温めた場合についてを考えてみます。熱容量の関係式は下記になります。
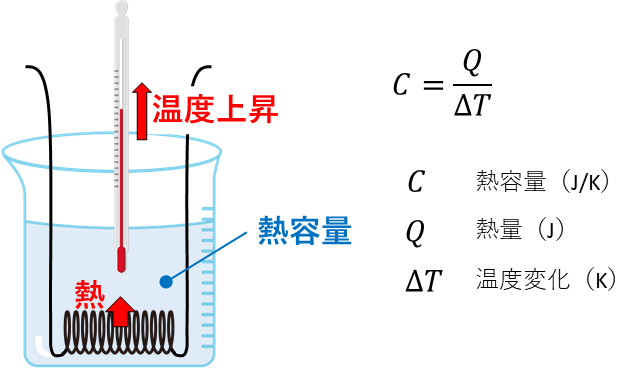
ここで、もしヒータの電源を切ると熱源がなくなり、ビーカーの液体は冷えていきます。よって、液体から熱が出ていくことも考慮しないといけません。
熱の出入りを考慮するため、流入する熱をQin、流出する熱をQoutと置き、温度上昇ΔTを計算する式に変形すると
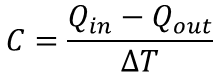
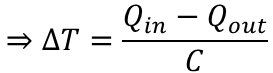
となります。ここでヒータから液体に流入する熱の流れ(単位時間あたりに流入する熱量)について考えてみます。ヒータで発生したジュール熱が全て液体に伝わったとすると

となります。ここでビーカーの液体から環境への熱の伝わりにくさについて考えてみます。これはオームの法則とのアナロジー(類推)から熱抵抗という概念を考えることができます。熱抵抗の単位はK/W(ケルビン・パー・ワット)となります。

上式はオームの法則の(電位差)=(電気抵抗)×(電流)という式によく似ていることが分かるかと思います。更に式を変形し液体から流出する熱の流れを計算すると
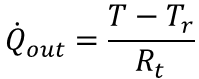
となります。ここで時間Δt(sec)だけ進んだ場合の温度変化ΔTを考えると下式のようになります。
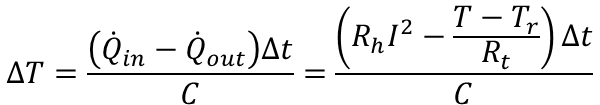
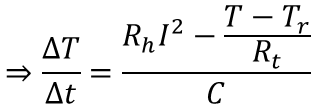
ここで、極限をとって微分方程式の形にすると下式になります。

これで熱が加わった(逃げた)際の温度変化を計算する式を微分方程式の形で書くことができました。
次回はこの微分方程式にある条件を加えて解いていきたいと思います。解いた式(解析解)は各パラメータが分かっていれば温度上昇(or 温度降下)が計算できるようになります。
更に式を変形し、途中までの昇温特性のデータしかない場合でも熱平衡状態の温度(到達温度)が計算できる式を求めていきます。
【微分方程式の活用】温度予測 どうやるの?②



