こんにちは、カヲルです!
今回は微分方程式を活用した温度予測の2回目の記事になります。前回は身近な温度予測の例として予測検温機能のついた体温計を挙げ、微分方程式を使って極簡単な数理モデルについて求めました。前回の記事を読まれていない方はこちらを確認お願いします。
【微分方程式の活用】温度予測 どうやるの?①
今回は前回求めた微分方程式を解き、途中までの温度上昇のデータから熱平衡状態の温度(到達温度)を求めていく方法について書きたいと思います。
では、手始めに前回求めた下式よりヒータをONにした時の温度上昇する場合の式とヒータをOFFにした場合の温度降下する場合の式を求めていきたいと思います。ここでは雰囲気温度(環境の温度)、印加電流、電気抵抗、熱抵抗、熱容量が一定(定数)として取り扱います。
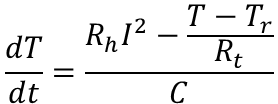
温度上昇の式(解析解)
前回求めた上式を変形していき、左辺に変数Tを集め、右辺に変数tを集めていきます。(変数分離)
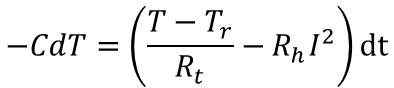
![]()
ここでCRtをギリシア文字のτ(タウ)に置き換えます。このτは熱時定数(ねつじていすう)とも呼ばれ、単位はsec(秒)となります。熱時定数とは熱的な応答の速さを示すものです。
![]()
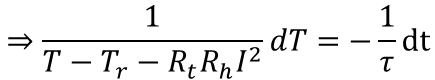
左辺と右辺で変数を分離することができました。ここで置換積分を応用し、両辺に積分記号を付けます。更にτは定数なので積分記号の外に出します。
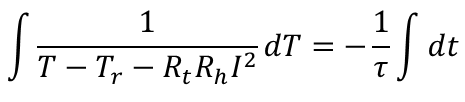
両辺を積分し、整理します。積分定数はAと置きます。
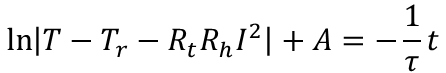
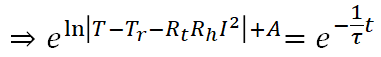
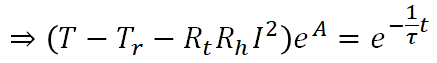
となります。ここでe^Aは定数のためBと置き換え、Bについて解くと
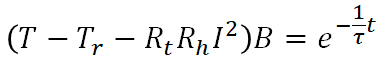
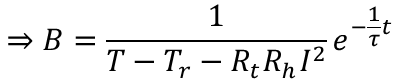
ここで初期(t=0)の時、ビーカーの液体の温度と室温は同じ(T = Tr)という初期条件を与えると
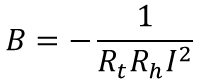
となります。Bを代入し式を整理すると
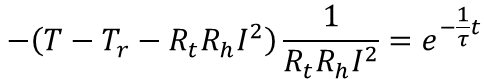
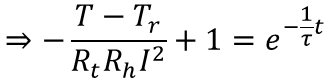
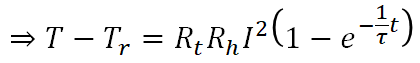
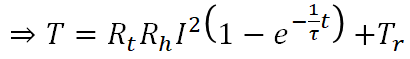
ここでt→∞の時の熱平衡状態(![]() )でのビーカーの液体の温度をTeと置くと
)でのビーカーの液体の温度をTeと置くと![]() であるから、
であるから、
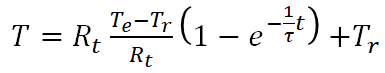
となります。よって温度上昇(昇温)の式は下式となります。
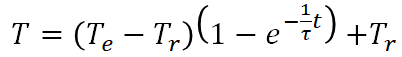
温度降下の式(解析解)
温度降下の式も前項で求めた式と途中までは同じです。(下式)
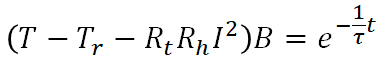
今回はヒータがOFFの時を想定するので電流I=0とすると、
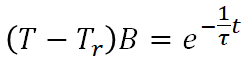
となります。t=0の時、ビーカーの液体の温度は熱平衡状態の温度Te(最大温度)であるとし、T=Teという初期条件を与えると
![]()
となり、Bについて解くと
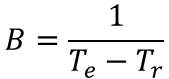
となります。Bを代入し、式を変形すると
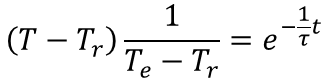
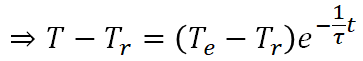
となります。よって温度降下(降温)の式は下式となります。
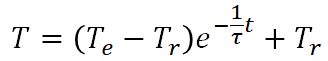
以上をまとめると下記のようになります。
雰囲気温度Tr、流入する熱の流れ(印加電流、電気抵抗)、熱時定数τ(熱抵抗、熱容量)が一定であり、熱平衡状態の温度をTeとするとある時刻tでの温度Tは下式で求められる。
(今回は例としてビーカーの液体をヒータで温めるものを考えましたが、上記が成り立つ場合は一般に成り立ちます。)
【温度上昇の式】
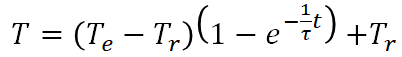
【温度降下の式】
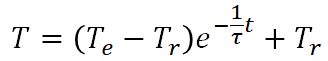
熱平衡状態の温度を求めよう!
ここからは予め実験するなどして熱時定数が既知の場合の昇温特性から熱平衡温度を求める方法について書いていきたいと思います。
熱平衡状態の温度の計算式
上記で求めた温度上昇の式から熱平衡状態の温度(到達温度)が計算できるように変形します。
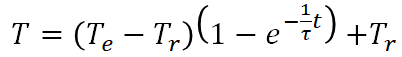
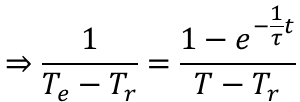
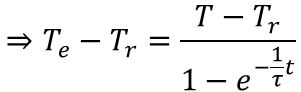
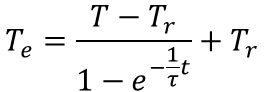
更に式を整理すると
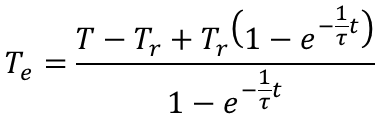
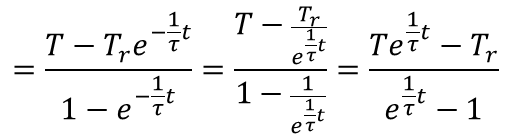
となります。
【熱平衡状態の温度の計算式】
雰囲気温度Trの環境下に於いて、ある時刻tのときの温度をTとすると熱平衡状態の温度(到達温度)Teは下式で表される。
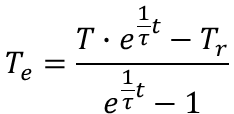
ここでτ(タウ)は熱時定数である。
熱平衡時の温度の計算
では実際に求めた式から熱平衡状態の温度(到達温度)を求めてみたいと思います。ここでは雰囲気温度、熱時定数は予め分かっているものとします。
先ず、検証用のデータを準備します。データは次の手順で準備します。(実験データがある場合はそれを使っても可)
1.Excelを起動し温度計のサンプリングレート、熱平衡状態の温度、雰囲気温度、熱時定数を決めます。この例ではサンプリングレート 2 S/sec、到達温度 36.89℃、雰囲気温度 23℃、熱時定数 120 secとしました。尚、サンプルリングレートは1秒当たりの測定数(サンプリング数)ですので、2 S/sec であれば0.5secごとにデータがサンプリングされることになります。
2.時間の進捗を入力するためにB12に0(ゼロ)を入力し、B13に”=B12+1/F$2″と入力します。B14以降はExcelのオートフィル機能を使ってB13の数式をコピーします。
3.先ほど入力した到達温度、雰囲気温度、熱時定数を用いて昇温特性をD列で計算します。D12に”=(F$3-F$4)*(1-EXP(-B12/F$5))+F$4″と入力し、D13以降は同様にオートフィル機能を使って数式をコピーします。
4.E列目に実際の実験データを模擬するために温度計のノイズ成分を計算します。ノイズは正規分布に従うものとします。E12に”=NORMINV(RAND(),0,D$7)”と入力し、同様にオートフィル機能を使って数式をコピーします。
5.F列はノイズ成分の乗った温度を計算します。F12に”=D12+E12″と入力し、同様にオートフィル機能を使って数式をコピーします。
これで、検証用のデータが準備できました。いよいよ到達温度を計算します。
G13に”=(F13*EXP(B13/F$5)-F$4)/(EXP(B13/F$5)-1)”と入力し、同様にオートフィル機能を使って数式をコピーします。これでサンプル時での時刻、温度から到達温度を計算できるようになりました。
以上の操作を行い、罫線等を引いて整理すると下図のようになります。
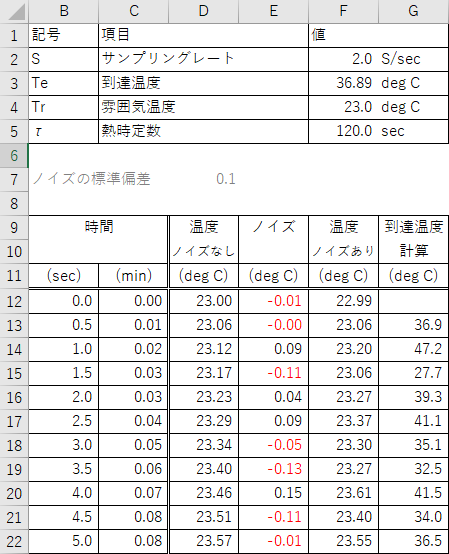
キーボードの[F9]ボタンを押すとExcelが再計算を行うので、押すたびにノイズ成分が入れ替わります。計算した昇温特性をグラフ化すると下図のようになります。実測データのようにしっかりノイズが載った自然なデータになっています。
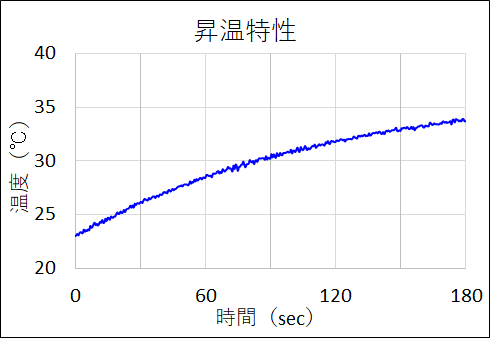
ここでG列で計算した各サンプル時での到達温度の計算結果をグラフ化してみます。
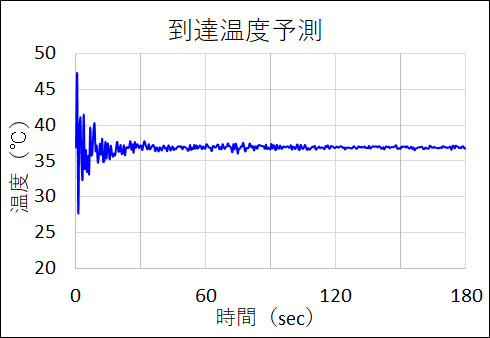
測定時間が伸びるほど正確な値が計算できていることが分かります。二点を結ぶような計算をしているので当然ですね。。。
60秒以降の計算結果を平均すればかなり正確な値が計算できます。
今回は熱時定数が分かっている場合について計算してみましたが、次回は実験から熱時定数を求める方法について書きたいと思います。
なお、今回 計算に用いたエクセルファイルは下記のリンクからダウンロードできます。



