
排気音がうるさいのでサイレンサーを改善したいのですが、どのようにしたらいいですか?
音は空気の振動として伝わるけど、電気回路での振動と対比(類推)させて考えれば、机上検討はある程度できるよ。

絞りの径や容積違いの試作品をたくさん作って、実験で確認してましたがパターンを絞れるのはよいですね!
ポンプやエンジンでは排気脈動により、騒音が発生します。本記事ではサイレンサーの基本的な設計方法について解説します。
音についての基本的な知識については下記記事を参考にしてみてください。
本記事では無料の電子回路シミュレータLTspiceを用いたサイレンサー(消音器)の設計方法と勘所について解説します。
Keywords|電気音響理論、アナロジー、拡張型消音器、電子回路シミュレータ、透過音、損失正接
サイレンサーの基礎理論

もし、「サイレンサーの基礎理論」の章が難しければ、読み飛ばしても大丈夫だよ!
電気音響理論
電気音響学(Electroacoustics)はアレクサンダー・グラハム・ベル(Alexander Graham Bell)によって発明され、電話用送受話器の動作機構を解析する手段として生まれました。
これは、電気回路の概念を応用して、音響現象を理解しようとする試みです。
電気音響学は、電話、ラジオ、テレビ、レコードプレーヤー、テープレコーダー、補聴器、魚群探知機、超音波加工機などの開発に応用され、音響学全体の発展に寄与してきました。
論理学で、物事の間の特定の点での類似性から、他の点での類似性を推論することをアナロジー(類推)と言いますが、本記事では上記の歴史的背景から電気振動系と音響振動系のアナロジーをメインに扱います。
音響振動系を考えるときに、機械振動系も頭の中にあったほうが理解しやすいから、機械振動系についても見ていくね!
機械振動系
振動を考える際に最も基本的な例は、機械振動系(バネ・マス・ダンパー系)です。
バネ・マス・ダンパー系のモデルをfig.1に示します。
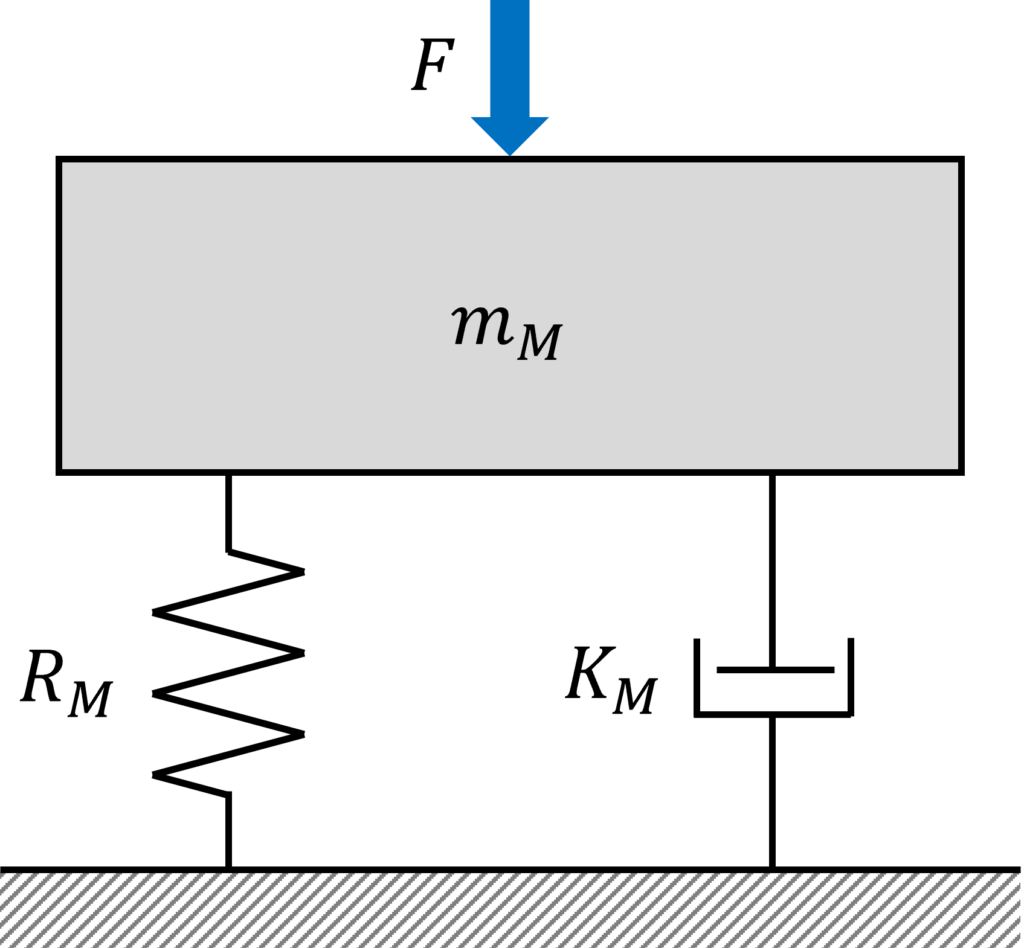
こちらは、下記の3つの要素からなります。なお、本記事では時間\((s)\)を\(t\)と置きます。
- マス
マスによる慣性力\(F_M \, (N)\)は、加速度\(a \, (m/s^2)\)に比例して働く。
慣性力と加速度を結ぶ比例定数は質量\(m_M \, (kg)\)と呼ばれる。
$$\begin{eqnarray}
F_M &=& m_M a \\
&=& m_M \frac{dv}{dt} \\
&=& m_M \frac{d^2 x}{d t^2} \tag{1}
\end{eqnarray}$$ - ダンパー
ダンパーによる抵抗力\(F_R \, (N)\)は、速度\(v \, (m/s)\)に比例して働く。
抵抗力と速度を結ぶ比例定数は減衰係数\(R_M \, (N \cdot s/m)\)と呼ばれる。
$$\begin{eqnarray}
F_R &=& R_M v \\
&=& R_M \frac{d x}{d t} \tag{2}
\end{eqnarray}$$ - バネ
バネによる弾性力\(F_K \, (N)\)は、変位\(x \, (m)\)に比例して働く。
弾性力と変位を結ぶ比例定数はバネ定数\(K_M \, (N/m)\)と呼ばれる。
$$F_K = K_M x \tag{3}$$
ここで、マスに加える力を\(F \, (N)\)と置くと、力のつり合い条件から下式が成り立ちます。
よって、Fig. 1の振動系の運動方程式は下式となります。
機械振動系の応用例として、振動を低減する防振ゴムなどがあるよ。
電気振動系
つぎに、電気振動系のモデルとしてRLC直列回路をFig.2に示します。
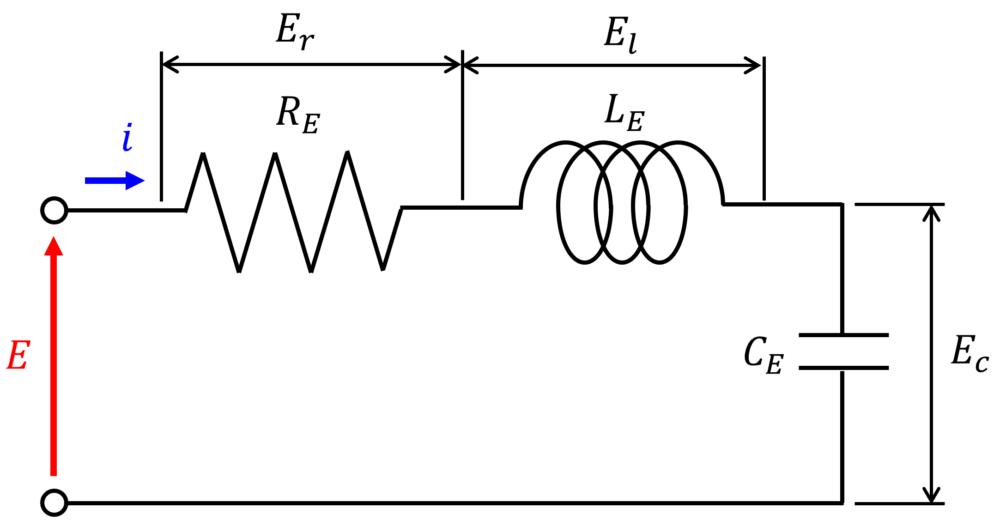
こちらも同様に、下記の3つの要素(素子)からなります。
- 抵抗器
抵抗器での電圧降下\(E_r \, (V)\)は、電流\(i \, (A)\)に比例する。
電圧と電流を結ぶ比例定数は電気抵抗\(R_E \, (\Omega)\)と呼ばれる。
$$E_r = R_E i \tag{6}$$ - コイル
コイルでの電圧降下\(E_l\, (V)\)は、電流の時間微分\(\frac{di}{dt} \, (A/s)\)に比例する。
電圧と電流の時間微分を結ぶ比例定数はインダクタンス\(L_E \, (H)\)と呼ばれる。
$$E_l = L_E \frac{di}{dt} \tag{7}$$ - コンデンサ
コンデンサでの電圧降下\(E_c\, (V)\)は、電流の時間積分\(\int idt \, (C)\)に比例する。
電圧と電流の時間積分を結ぶ比例定数はキャパシタンス(静電容量)\(C_E \, (F)\)と呼ばれる。
$$E_c = \frac{1}{C_E} \int idt \tag{8}$$
キルヒホッフの第二法則より、直列接続されているコイルでの電圧降下、抵抗器での電圧降下、コンデンサでの電圧降下の総和が外部から印加した電圧\(E \, (V)\)と等しくなるため、下式が成り立ちます。
よって、Fig.2の振動系の方程式は下式となります。
ここで、電荷を\(q \, (C)\)と置くと、\( i = \frac{dq}{dt} \)より下式が成り立ちます。
もし電気回路自体にご興味がある方は、最近はオンライン学習サイトもあるので、そちらも覗いてみても面白いかも知れません。検索で「回路」と打つと、興味をそそられる動画がたくさんあります。
世界最大級のオンライン学習サイトUdemy機械振動系・電気振動系のアナロジー
機械振動系の式(5)と電気振動系の式(11)を比較すると、式の形がよく似ていることに気づきます。
これが機械振動系と電気振動系のアナロジーになります。対照表を下表に示します。
| 機械振動系 | 電気振動系 | |
|---|---|---|
| 慣性要素 \( m \) | 質量 \(m_M \, (kg)\) | インダクタンス \(L_E \, (H)\) |
| 抵抗要素 \( R \) | 減衰係数 \(R_M \, (N \cdot s/m)\) | 電気抵抗 \(R_E \, (\Omega)\) |
| 弾性要素 \( K \) | バネ定数 \(K_M \, (N/m)\) | エラスタンス \( \frac{1}{C_E} \, (F^{-1})\) |
| 弾性要素 \( \frac{1}{K} \) | 機械的コンプライアンス \( \frac{1}{K_M} \, (m/N)\) | キャパシタンス \(C_E \, (F)\) |
| 交番変数 \( x \) | 変位 \(x \, (m)\) | 電荷 \(q \, (C)\) |
| 交番変数 \( \frac{dx}{dt} \) | 速度 \(v \, (m/s)\) | 電流 \(i \, (A)\) |
| 交番外力 \( f \) | 力 \(F \, (N)\) | 電圧 \(E \, (V)\) |
なお、上表の機械的コンプライアンスとエラスタンスは、工学の世界では使用頻度が少ない言葉ですので水色で目立たなくしています。
機械振動系や電気振動系のモデル化(数式化)は制御工学で詳しく勉強できるよ。詳しく知りたい人は図書館などで借りて読んでみてね!
音響振動系
電気振動系では、インダクタンス・電気抵抗・キャパシタンスがありましたが、音響振動系ではそれらに相当するものとして、音響イナータンス・音響抵抗・音響コンプライアンスの3つの要素(音響素子)があります。
音響振動系は少し特殊なので、ここからは1つずつ順番に見ていきます。

Fig.3に示す通り、断面積\(S \, (m^2)\)、長さ\(l \, (m)\)の管を考えます。
このとき、管の長さが音の波長より十分に小さい場合は、管の気体が一体となって速度\(v \, (m/s)\)で運動しているとみなすことができます。
よって、気体の密度を\(\rho \, (kg/m^3)\)と置くと、管内の気体の質量\(m \, (kg)\)は下式となります。
ここで、管の片方の断面に圧力\(p \, (Pa)\)が働いたととき、管内の気体の運動方程式を考えると、力\(pS \, (N)\)が働くため、
となります。コイルの電圧降下を表す式(7)とのアナロジーから、音響イナータンス\(m_A \, (kg/m^2)\)は
となります。
Fig.3に示す管が細くなると、気体と管内壁との摩擦力(粘性力)の影響が無視できなくなります。
いま、\(l\)が十分に長い円管について考えると、円管内の気体は円管ポアズイユ流れで運動していると考えることができ、円管の半径を\(r \, (m)\)、気体の体積速度を\(u \, (m^3/s)\)、気体の粘性係数を\(\mu \, (Pa \cdot s)\)と置くと下式が成り立ちます。
ここで、粒子速度を\(v \, (m/s)\)と置くと、体積速度は\(u\)は
と定義できるため、式(16)と式(17)より
となります。よって、抵抗器の電圧降下を表す式(6)とのアナロジーから、音響抵抗\(R_A \, (Pa \cdot s/m)\)は
となります。
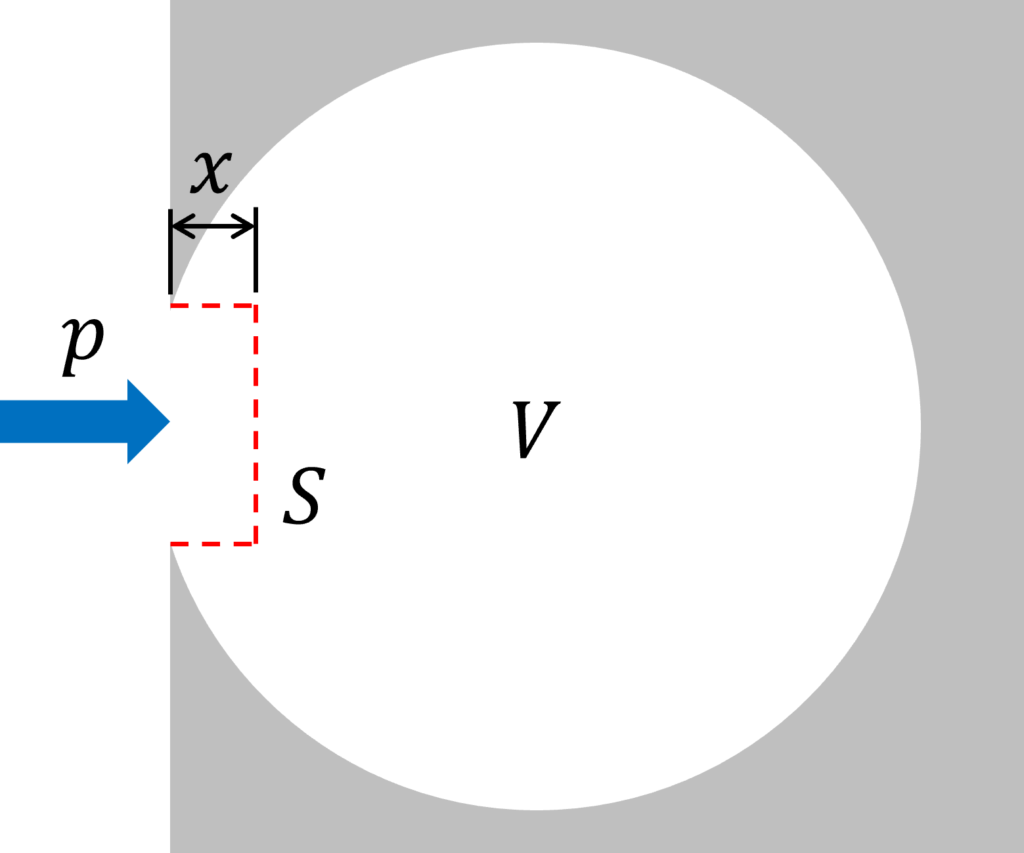
Fig.4に示すような、体積\(V \, (m^3)\)の小空洞に断面積\(S \, (m^2)\)の開口部のある容器を考えます。
容器のサイズが音の波長より十分に小さい場合は、気体が一体となって運動しているとみなすことができます。
ここで、容器内の気体が断熱変化していると考え、比熱比を\(\kappa\)と置くとポアソンの法則より
となります。上式を全微分すると
となります。ここで、外部圧力\(p_0 \, (Pa)\)を基準圧力とし、基準圧力からの変動成分\(dp = p\)と書き換えると
となります。ここで、体積変化\(dV\)は下式で表すことができます。
式(27)に式(29)を代入すると
となり、\(u = Sv\)より
となります。ここで、音速\(c = \sqrt{ \frac{\kappa p_0}{\rho}}\)より
となります。よって、コンデンサの電圧降下を表す式(8)とのアナロジーから、音響コンプライアンス\(C_A \, (m^3/N)\)は
となります。
もし、全微分があやしければ、こちらで復習してみてね。
機械振動系・電気振動系・音響振動系のアナロジー
Table 1でまとめた対照表に音響振動系を追加すると、下表のようになります。
| 機械振動系 | 電気振動系 | 音響振動系 | |
|---|---|---|---|
| 慣性要素 \( m \) | 質量 \(m_M \, (kg)\) | インダクタンス \(L_E \, (H)\) | 音響イナータンス \(m_A \, (kg/m^2)\) |
| 抵抗要素 \( R \) | 減衰係数 \(R_M \, (N \cdot s/m)\) | 電気抵抗 \(R_E \, (\Omega)\) | 音響抵抗 \(R_A \, (Pa \cdot s/m)\) |
| 弾性要素 \( K \) | バネ定数 \(K_M \, (N/m)\) | エラスタンス \( \frac{1}{C_E} \, (F^{-1})\) | 音響スティフネス \( \frac{1}{C_A} \, (N/m^3)\) |
| 弾性要素 \( \frac{1}{K} \) | 機械的コンプライアンス \( \frac{1}{K_M} \, (m/N)\) | キャパシタンス \(C_E \, (F)\) | 音響コンプライアンス \(C_A \, (m^3/N)\) |
| 交番変数 \( x \) | 変位 \(x \, (m)\) | 電荷 \(q \, (C)\) | 変位 \(x \, (m)\) |
| 交番変数 \( \frac{dx}{dt} \) | 速度 \(v \, (m/s)\) | 電流 \(i \, (A)\) | 粒子速度 \(v \, (m/s)\) |
| 交番外力 \( f \) | 力 \(F \, (N)\) | 電圧 \(E \, (V)\) | 圧力 \(p \, (Pa)\) |
音響素子のサイレンサーへの応用
内燃機関やポンプなどのサイクル動作している流体機械では排気脈動があり、そのまま大気解放するとその脈動により大きな騒音を生じます。
その対策としては、通常はFig.5に示すように排気管(排気通路)に断面積変化をつけた拡張型消音器(サイレンサー)を設けます。
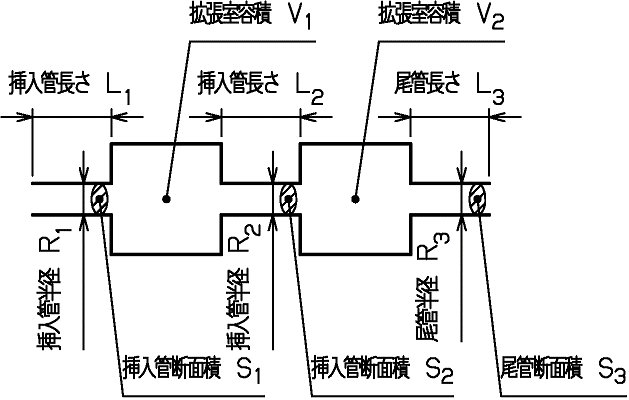
この拡張型消音器は、任意の周波数特性をもつ伝達系として機能しており、これは一種の音響フィルタとなります。
よって、音響イナータンス・音響抵抗・音響コンプライアンスの3つ音響素子を使って周波数特性を解析することができます。
本記事では、電気振動系と音響振動系のアナロジーを用い、Fig.5をFig.6のような等価回路に変換し、解析していく手法について解説します。
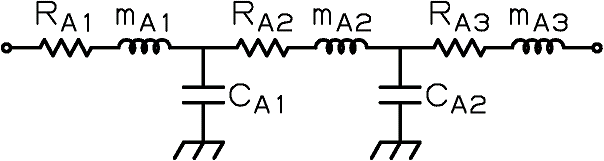
電気回路のフィルタの設計もいろいろ書籍が出ているので、合わせて見てみるのもよいかもね!
サイレンサーの容積、絞りの設計

では、実際に例題を解いてみたいと思います。なお、尾管から測定室に接続されているものとします。
下記の消音器の周波数特性を求めよ。なお、空気密度\( \rho = 1.205 \, (kg/m^3) \)、空気の粘性係数\( \mu = 1.822 \times 10^{-5} \, (Pa \cdot s) \)、音速\( c = 343.5 \, (m/s) \)とする。
- 挿入管半径 \( r_1 = 1.5 \, mm\)、挿入管長さ \( l_1 = 7 mm\)
- 拡張室容積 \( V_1 = 30,000 \, mm^3 \)
- 挿入管半径 \( r_2 = 1.5 \, mm\)、挿入管長さ \( l_2 = 10 mm\)
- 拡張室容積 \( V_2 = 50,000 \, mm^3 \)
- 尾管半径 \( r_3 = 1.5 \, mm\)、尾管管長さ \( l_3 = 5 mm\)
- 測定室容積 \( V_3 = 75 \, m^3 \)

回路定数の計算
まず、式(15)より挿入管1の音響イナータンスを求めます。
つぎに、式(20)より挿入管1の音響抵抗を求めます。
最後に、式(33)より挿入管1の音響コンプライアンスを求めます。
同様の手順で挿入管2、尾管、測定室の回路定数を求めると以下の様になります。
| 記号 | 項目 | 値 |
|---|---|---|
| $$m_{A1}$$ | 挿入管1の音響イナータンス | $$ 8.44 \times 10^{-3} \ \ (kg/m^2) $$ |
| $$R_{A1}$$ | 挿入管1の音響抵抗 | $$ 453 \times 10^{-3} \ \ (Pa \cdot s/m) $$ |
| $$C_{A1}$$ | 挿入管1の音響コンプライアンス | $$ 29.9 \times 10^{-6} \ \ (m^3/N) $$ |
| $$m_{A2}$$ | 挿入管2の音響イナータンス | $$ 12.1 \times 10^{-3} \ \ (kg/m^2) $$ |
| $$R_{A2}$$ | 挿入管2の音響抵抗 | $$ 648 \times 10^{-3} \ \ (Pa \cdot s/m) $$ |
| $$C_{A2}$$ | 挿入管2の音響コンプライアンス | $$ 49.8 \times 10^{-6} \ \ (m^3/N) $$ |
| $$m_{A3}$$ | 挿入管3の音響イナータンス | $$ 6.03 \times 10^{-3} \ \ (kg/m^2) $$ |
| $$R_{A3}$$ | 挿入管3の音響抵抗 | $$ 324 \times 10^{-3} \ \ (Pa \cdot s/m) $$ |
| $$C_{A3}$$ | 挿入管3の音響コンプライアンス | $$ 74.6 \ \ (m^3/N) $$ |
シミュレータのインストール(無料)
前項までで、それぞれの回路定数を求めることが出来ました。
では、実際に回路図を作成し、シミュレーションを実行しようと思います。
電子回路シミュレータはたくさんありますが、本記事では業務でも使えるほど高機能であるにも関わらず、完全無料で使えるLTspiceを使っていこうと思います。
下のリンクより、開発元のAnalog Devices(アナログ・デバイセズ)のWEBサイトに移動します。
https://www.analog.com/jp/design-center/design-tools-and-calculators/ltspice-simulator.html
「Windows7、8、10の64ビット版をダウンロード」をクリックし、ダウンロードします。
ダウンロードが完了したら、インストールしましょう。
下の記事でもLTspiceのインストール方法を1つ1つ手順を追って解説しているよ!
シミュレーションの実行
インストールが完了したら、先ずはいろいろ操作してソフトに慣れてみよう。
もし、LTspiceの使い方が分からない人は、下の記事を参考にしてね!
簡単な回路を例題として、1つ1つ手順を追って解説してるよ。

言葉の意味やExcelへのデータのインポート方法も解説されてますね。
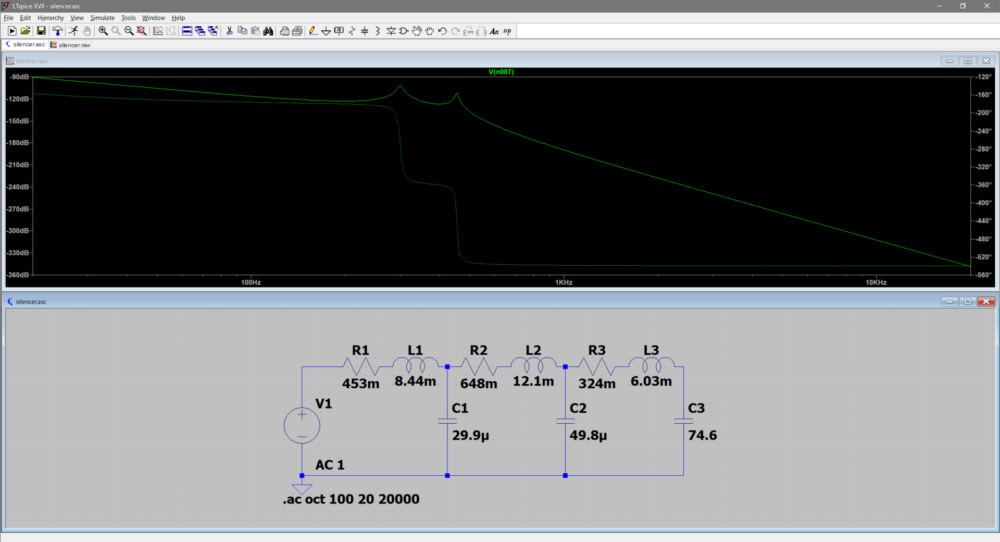
回路定数の計算結果(Table 3)を元にLTspiceにて回路図を作成します。下の画面の様に部品を配置します。
音響イナータンスをインダクタンス、音響抵抗を電気抵抗、音響コンプライアンスをキャパシタンスに置き換え、回路定数を設定していきます。
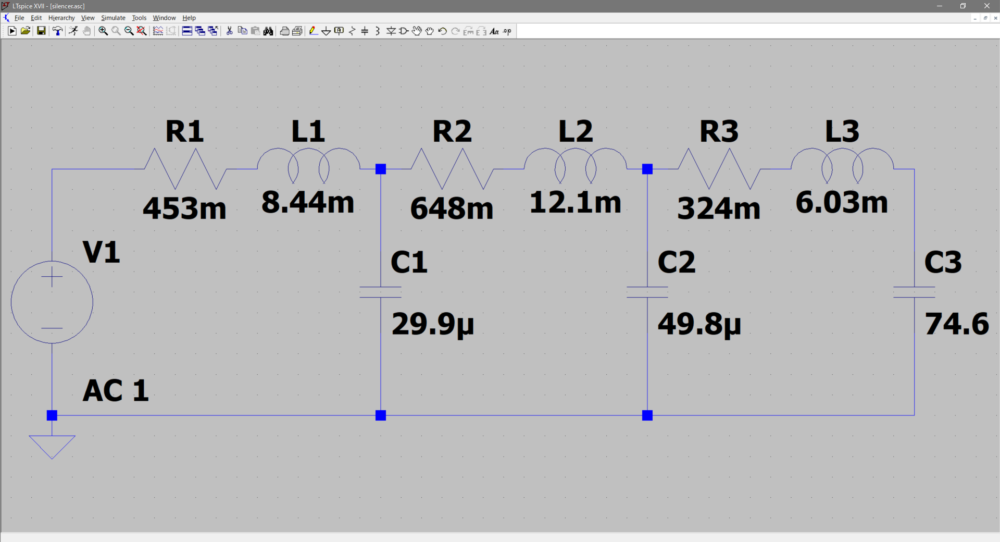
Sweep(掃引)する範囲はヒトの可聴周波数である20Hzから20,000Hzに設定します。
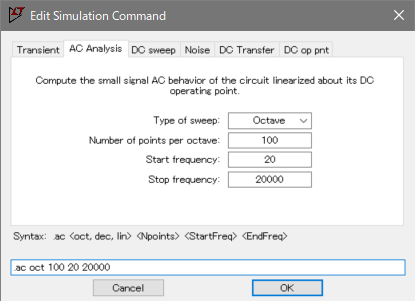
下の画面の回路図にマウスポイントを合わせるとプローブマークになります。
L3とC3の間をクリックすると、上の画面(ボード線図)にてサイレンサーの周波数特性が確認できます。
まとめ
最後に本記事のまとめをしておしまいにしたいと思います。
- 電気音響理論を用いて、サイレンサーを音響素子に置き換えて解析することができる。
- 機械振動系、電気振動系、音響振動系はアナロジーがある。
- アナロジーを用いて、音響振動系は電子回路シミュレータで解析することができる。
- 電子回路シミュレータはLTspiceが高機能かつ無料である。
さらに勉強をしたい人は音響学や振動学の本を見てみてね。
内容(「BOOK」データベースより)
吸音材やダンピング材などを使用した受動的(パッシブ)な消音・制振対策やディジタル信号処理を用いた能動的(アクティブ)な騒音・振動制御、適切な付加音やリズムの改善など、「快音」を目指すための技術と理論を分かりやすくまとめました。エレベータやヘッドホン、冷蔵庫、鉄道、建物、自動車、カメラ、コピー機など、さまざまな分野で採用されている静音・快音のための技術を具体的に解説し、これらの技術の基礎となる音響・振動、ディジタル信号処理の基礎理論まで概説した一冊です。
内容(出版社HPより)
生理,心理,可聴音より超音波までの理論と実用例,更に騒音とその制御までを含んでいる本書は,著者らが多年の経験を基に各専門に基づき平易にまとめたもの。
内容(「MARC」データベースより)
機械系の学生、技術者を対象に音響学の基礎を解説する。各章末に演習問題も付す。著者が企業で行った研修資料と大学で行った講義のノートをもとにして、企業との共同研究の資料を追加してまとめる。








