【MATLAB】Simulink上で行列を計算しよう！

本記事ではMATLAB/Simlinkを使った行列の計算方法について解説します。

スクリプト(mファイル）を使ったものは多く見かけますが、Simulinkのブロックを使う場合の解説は意外と少ないので、基本的なところから解説していきます。

現代制御理論（Modern control theory）を使ったモデル化などの基礎知識として役立てて頂ければと思います。

線形代数関連記事

2021年5月5日スッキリ解決！線形代数何に使うの？（社会での応用例）

Simulinkの操作の基本

行列の配置①（定数の場合）

まず、スカラーの場合と同様に[Simulink ライブラリブラウザー]を開き、[Sources]の[Constant]を選択します。

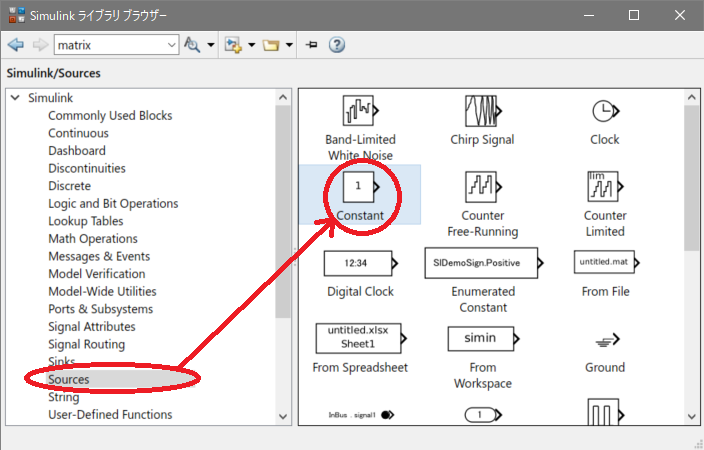
[モデルブラウザー]にドラック＆ドロップし配置します。Constantブロックを配置したら、ブロックをダブルクリックし、[ブロックパラメーター]ウィンドを表示させます。

行列を定義する際のルールはスクリプトの場合と同様です。以下のルールに従います。

行列の定義のルール（文法）

行列および列ベクトル（１列のみの行列）、行ベクトル（１行のみの行列）を定義する際は最初と最後をカッコ [ ] で囲む。
行列の成分同士（数値や変数）はスペースで区切る。
行と行の間はセミコロン（ ; ）で区切る。

では、実際に行列を定義してみましょう。
例として以下のような３行３列の行列を入れてみます。

$$ \begin{bmatrix} 2 & 3 & 1 \\ 1 & 1 & -1\\ 3 & 1 & 1\\ \end{bmatrix}\\ $$

上記のルールに従い、[定数値]のテキストボックスに数値を入力します。

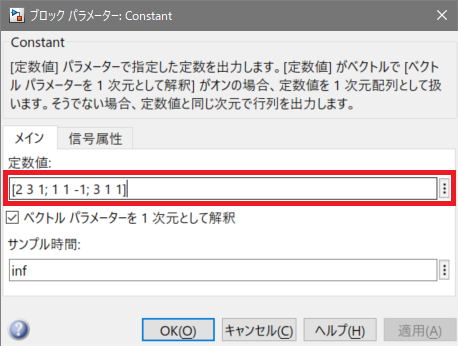
[OK]ボタンを押下すると以下のように表示されます。

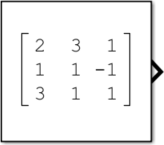
ブロックの大きさはマウスで自由に変えられるので、見やすい大きさにしましょう。

行列の要素の確認方法

Displayブロックを使うと行列の中身が確認できます。
下図はDisplayブロックと結線し、[実行]ボタンを押下した後の状態です。

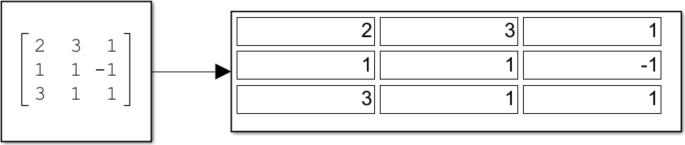
行列の配置②（変数の場合）

行列の要素の一部を変数とする場合は行列の積と和で実現する方法もありますが、[User-Defined Functions]の[MATLAB Function]ブロックを使う方法が簡単です。

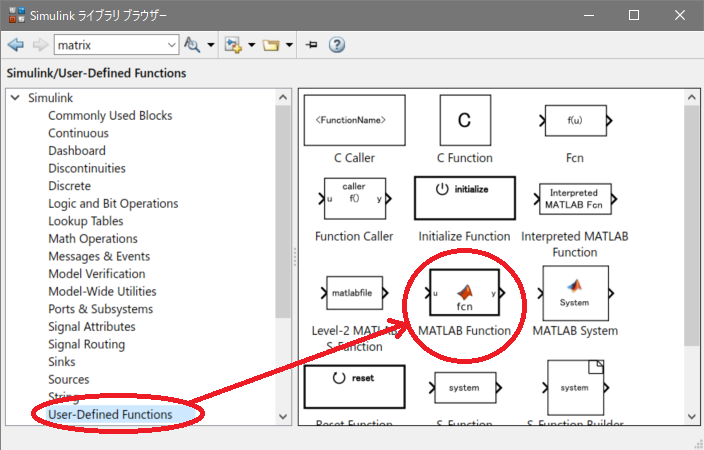
Constantブロックと同様に[モデルブラウザー]にドラック＆ドロップし、MATLAB Functionブロックをダブルクリックします。そうするとエディターの画面に移ります。

表示された[エディター]にはフレームとなる入力例が予め入っていますが、先ほどの例題の一部を変数としたものを定義してみましょう。

function A = fcn(u, v)
A = [v 3 1;
　　u 1 -1;
　　1 u 1;]

予め入力されているものを上記のように修正し、[モデルブラウザー]に戻ると、$u$と$v$を入力変数（引数）とし、行列$A$を出力変数（戻り値）とするブロックが出来上がっていると思います。

ConstantブロックとDisplayブロックを下図のように接続し、[実行]ボタンを押下すると先ほどの例と同様の状態となります。

なお、Constantブロックに入力する値は、今度はスカラーですので数字のみ入力してください。

カヲル

せっかく変数にしたので、いろいろ値を変更して遊んでみてね！

行列の和、差

行列の和、差は[Add]ブロックや[Sum]ブロックが使えます。この例題ではSumブロックを使ってみましょう。

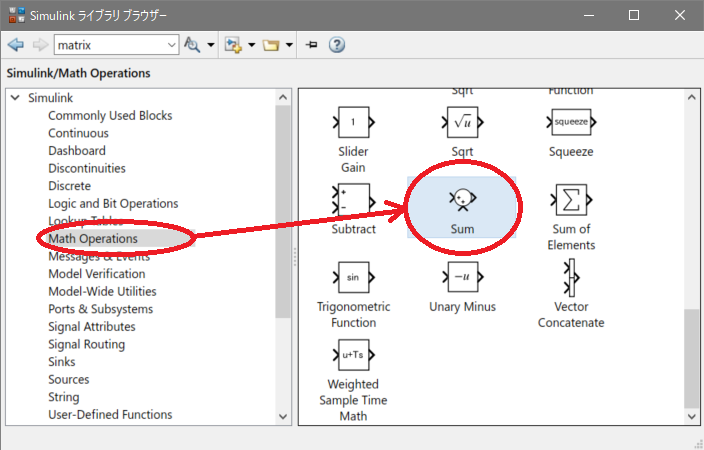
以下の計算をしてみます。

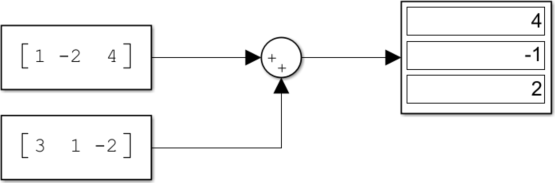
$$ \begin{bmatrix} 1\\ -2\\ 4\\ \end{bmatrix} + \begin{bmatrix} 3\\ 1\\ -2\\ \end{bmatrix} = \begin{bmatrix} 4\\ -1\\ 2\\ \end{bmatrix}\\ $$

Constantブロック、Sumブロック、Displayブロックを結線し、[実行]ボタンを押下すると下図のようになります。
Costantブロックの列ベクトルは、表示上は一列に要素が表示されない仕様であることは注意してください。

なお、行列の差を計算する場合は、Sumブロックをダブルクリックし、[符号リスト]の$+$記号を$-$記号に変更してください。

記号の$+, \, -$は入力された順にSumブロックの入力が設定されます。

行列のスカラー倍

行列のスカラー倍は[Gain]ブロックが使用できます。

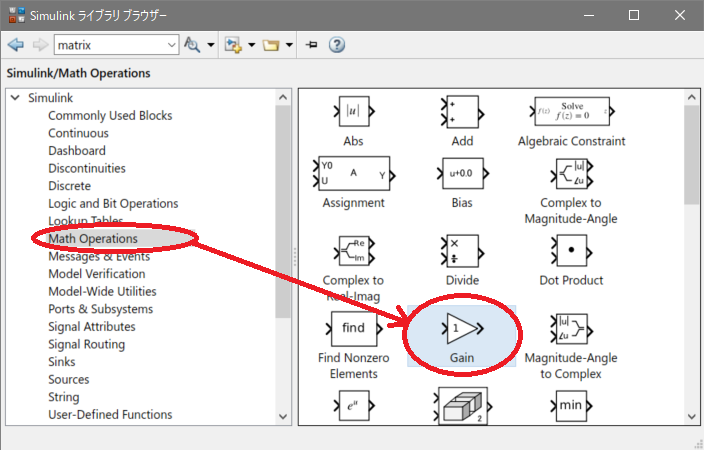
以下の計算をしてみます。

$$ 2 \begin{bmatrix} 2 & 3 & 1 \\ 1 & 1 & -1\\ 3 & 1 & 1\\ \end{bmatrix} = \begin{bmatrix} 4 & 6 & 2 \\ 2 & 2 & -2\\ 6 & 2 & 2\\ \end{bmatrix}\\ $$

Gainブロックを[モデルブラウザー]にドラック＆ドロップし、Gainブロックをダブルクリックします。[Gain:]のテキストボックスにかける数値を入力します。

Constantブロック、Gainブロック、Displayブロックを結線し、[実行]ボタンを押下すると下図のようになります。

カヲル

[Gain:]のテキストボックスはマイナスの数字を入れることもできるよ！

行列の積

行列の積は[Quick Operations] – [Math Operations] – [Matrix Multiply]を使用します。

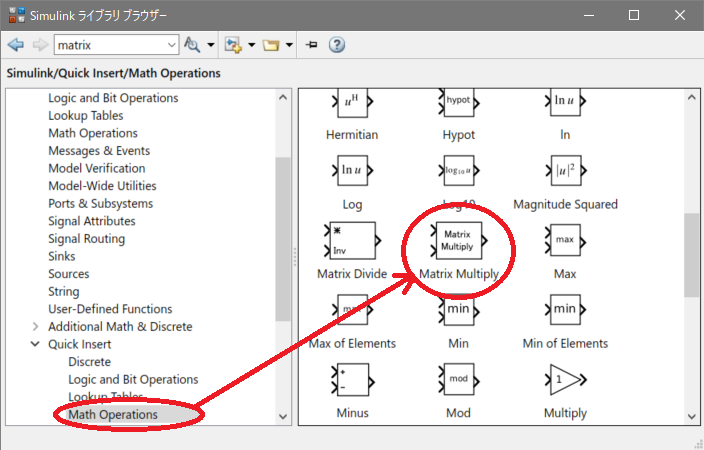
以下の計算をしてみます。

$$ \begin{bmatrix} 1 & 2\\ 3 & 4\\ \end{bmatrix} \begin{bmatrix} 3 & 4 & 2\\ 1 & 2 & 3\\ \end{bmatrix} = \begin{bmatrix} 5 & 8 & 8\\ 13 & 20 & 18\\ \end{bmatrix}\\ $$

Constantブロック、Matrix Multiplyブロック、Displayブロックを結線し、[実行]ボタンを押下すると下図のようになります。

逆行列

逆行列（Inverse matrix）は[Quick Operations] – [Math Operations] – [Matrix Divide]を使用します。

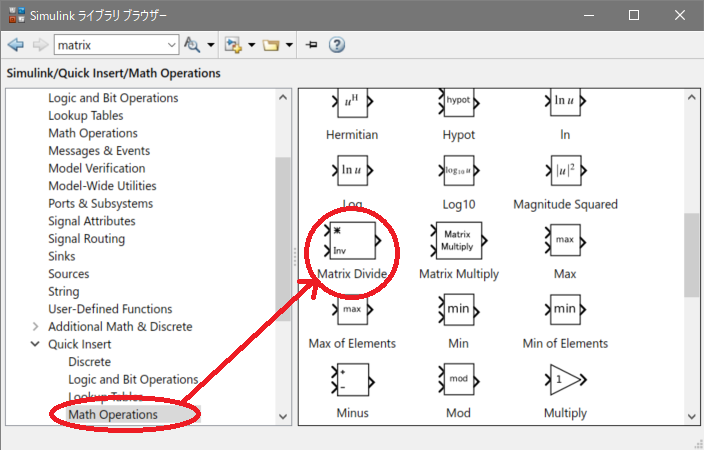
このブロックは積と逆行列を求められるようになっています。

このブロックをダブルクリックすると[入力数:]のテキストボックスにデフォルトで */ と入力されており、逆行列との積を計算するようになっています。（但し、行列の計算は順番が重要なので注意！！）

心太

* は積（掛け算）の記号、 / は商（割り算）の記号ですね。

カヲル

[入力数:]のテキストボックスに ** と入力すると、[Matrix Multiply]ブロックに化けるので中身は同じものだよ！

以下のような行列$A$の逆行列$A^{-1}$を計算をしてみます。

$$\begin{eqnarray} A\,\,\,\,\,\,\,&=& \begin{bmatrix} 2 & 3 & 1 \\ 1 & 1 & -1\\ 3 & 1 & 1\\ \end{bmatrix}\\ \\ A^{-1}&=& \begin{bmatrix} -0.2 & 0.2 & 0.4 \\ 0.4 & 0.1 & -0.3\\ 0.2 & -0.7 & 0.1\\ \end{bmatrix}\\ \end{eqnarray}$$

Matrix Divideブロックを[モデルブラウザー]にドラック＆ドロップし、Matrix Divideブロックをダブルクリックします。[入力数:]のテキストボックスに演算子を入力します。

ここでは逆行列を計算するので、下図のように / のみ入力しましょう。

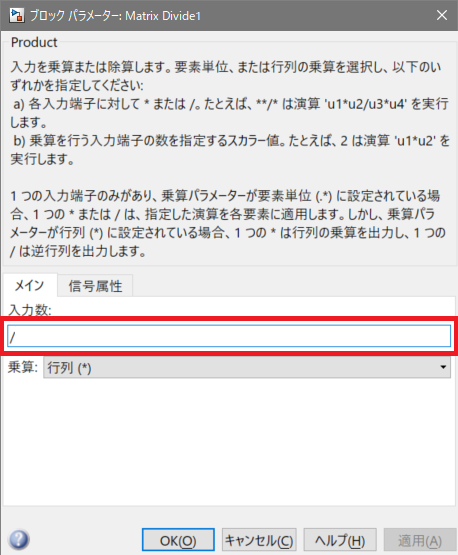
Constantブロック、Matrix Divideブロック、Displayブロックを結線し、[実行]ボタンを押下すると下図のようになります。

転置

転置（Transpose）は[Quick Operations] – [Math Operations] – [Transpose]を使用します。

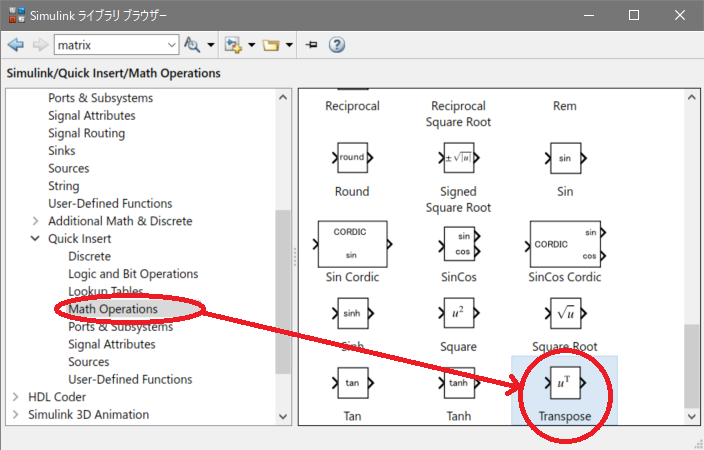
以下のような行列$A$の転置行列$A^{T}$を計算をしてみます。

$$\begin{eqnarray} A\,\,\,\,&=& \begin{bmatrix} 2 & 3 & 1 \\ 1 & 1 & -1\\ 3 & 1 & 1\\ \end{bmatrix}\\ \\ A^{T}&=& \begin{bmatrix} 2 & 1 & 3 \\ 3 & 1 & 1\\ 1 & -1 & 1\\ \end{bmatrix}\\ \end{eqnarray}$$

Constantブロック、Transposeブロック、Displayブロックを結線し、[実行]ボタンを押下すると下図のようになります。

線形代数関連記事

線形代数の応用分野として人工知能（AI）について分かりやすく解説します。

2022年7月31日分かりやすく解説！人工知能、機械学習とは

行列を使った連立一次方程式の計算

行列式

行列$A$に逆行列$A^{-1}$が存在する条件は$|A| \neq 0$であり、このときの行列を正則行列と言います。

このあと、逆行列を用いて連立一次方程式を解きますが、解が一つに定まる条件として正則行列になっている必要があります。

ここでは、例題として以下のような行列$A$の行列式$|A|$を計算をしてみます。

$$\begin{eqnarray} A \,\, &=& \begin{bmatrix} 2 & 3 & 1 \\ 1 & 1 & -1\\ 3 & 1 & 1\\ \end{bmatrix}\\ \\ |A|&=& -10 \\ \end{eqnarray}$$

Simulinkでは行列式（Determinant）を求める専用のブロックは用意されていないため、[User-Defined Functions]の[MATLAB Function]ブロックを使用します。

ブロックを配置したら、ダブルクリックして[エディター]を表示して以下のようにスクリプトを修正します。

function y = fcn(u)
y = det(u);

Constantブロック、MATLAB Functionブロック、Displayブロックを結線し、[実行]ボタンを押下すると下図のようになります。

カヲル

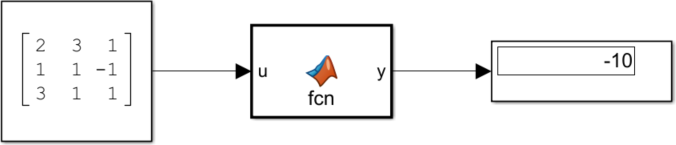
今回はdet関数で行列式を計算したけど、rank関数で行列のランクを求めることもできるよ！

連立一次方程式

ここでは、以下のような連立一次方程式を解いてみたいと思います。

$$ \left\{ \begin{array}{l} 2x_1 +3x_2 + x_3 = 1 \\ x_1 + x_2 \,-\, x_3 = -2\\ 3x_1 + x_2 + x_3 = 4 \end{array} \right.\\ $$

上式を行列・ベクトル表示にすると

$$ \begin{bmatrix} 2 & 3 & 1 \\ 1 & 1 & -1\\ 3 & 1 & 1 \end{bmatrix} \begin{bmatrix} x_1\\ x_2\\ x_3 \end{bmatrix} = \begin{bmatrix} 1\\ -2\\ 4 \end{bmatrix} \\ $$

となります。上式を$A \, \textbf{x} = \textbf{b}$と書くと、係数行列$A$が正則であれば、

$$ \textbf{x} = A^{-1} \, \textbf{b}\\ \\ $$

として未知数ベクトル$\textbf{x}$を解くことができます。

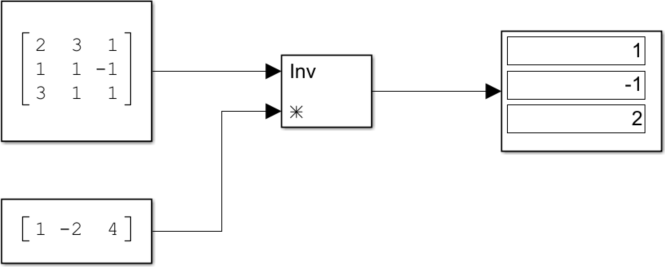
では、実際にMATAB/Simlinkにて解いてみたいと思います。Constantブロックにて係数行列$A$と定数項ベクトル$\textbf{b}$を用意し、Matrix Divideブロックを配置します。

Matrix Divideブロックをダブルクリックし、[入力数:]のテキストボックスに \* とに入力します。（演算子の順番注意！）

それぞれを結線し、[実行]ボタンを押下すると下図のようになります。