こんにちは、カヲルです!
機械設計者が流体機械を設計する場合、熱流体解析ソフト(数値流体力学, CFD : Computational Fluid Dynamics)を用いて設計検討する場面があるかと思います。
応力や変位などを求める構造解析ソフトと異なり、背景にある物理を理解していないと何をしたらよいか分からないことも多いように思います。
もちろん、構造解析ソフトを使用する場合も背景にある物理を理解していないと解析結果を検証し、正しい答えを出せないとは思いますが、熱流体解析のほうがハードルが高く感じている人が多いように思います。
そこで今回は少しでも敷居を下げるために流体力学で習う連続の式(equation of continuity)について簡単に分かりやすく解説していきたいと思います。
はじめに

流体力学とは
空気、天然ガス、水、オイル、ガソリンなどに代表される気体(Gas)と液体(Liquid)を総称して流体(Fluid)と言います。
流体の特徴として固体(Soild)と比べてわずかな力で変形し、運動する性質を持っています。
この運動を流体の流れと言い、自動車のボデーや飛行機の翼の周りの流れなど物体の外部の流れを外部流れ(External flow)、配管やターボ機械などの内部の流れを内部流れ(Internal flow)と言います。
流体力学(Fluid dynamics)はこれらの流れの挙動を解析する学問になります。
流体力学で用いる物理法則(支配法則)
流体力学の背景にある物理法則は質量保存則(mass conservation law)と運動量保存則(momentum conservation law)になります。
連続の式は流体力学における質量保存則になります。
なお、熱の移動も考慮する場合はエネルギー保存則も入れる必要があります。
1.質量保存則(連続の式)
外部とやりとりがされない限り質量は変化しないという法則。
元々は「化学反応の前後で物質の質量は変化しない」という化学の法則になります。
現在では質量はエネルギーの一形態であると知られおり必ずしも保存しませんが、実用上便利な法則であり流体力学でも用いられます。
2.運動量保存則(ナビエ・ストークス方程式)
外部から力が働かない限り運動量(質量と速度の積)は変化しないという法則。
流体力学での運動量保存則を表すナビエ・ストークス方程式はニュートンの運動方程式を応用したものになります。
本記事ではこちらの説明は対象外とします。
3.エネルギー保存則(エネルギー方程式)
外とエネルギーがやり取りされない限りエネルギーは変化しないという法則。
こちらは熱力学第一法則を応用したものになります。
本記事ではこちらの説明も対象外とします。
 超・基礎から解説!ナビエ・ストークス方程式の導出【流体力学】
超・基礎から解説!ナビエ・ストークス方程式の導出【流体力学】
 【圧縮性流体力学】エネルギー方程式とモデルベース開発(MBD)
【圧縮性流体力学】エネルギー方程式とモデルベース開発(MBD)
連続の式に関連する物理量
流体の単位体積あたりの質量を密度(Density)と言います。
流体の体積をV(m^3)、質量をm(kg)と置くと密度ρ(kg/m^3)は下式になります。
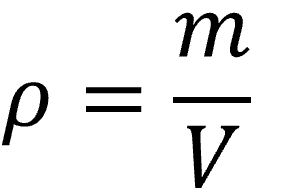
流体の流れの速さを流速(Flow velocity)と言います。流速v(m/s)は任意の位置r(m)と時間t(s)の関数で表されます。

高校や大学一年生で習う質点もしくは剛体の運動と異なり、流体力学はある決まった場所での流速や圧力などに興味の対象があるため、このような定義の仕方をします。
大学以降では太字で書いたものがベクトル、細字で書いたものがスカラーだよ。また、流速はvと置いたけど、uで置いている教科書も多いよ。
単位時間あたりに流れる流体の体積を体積流量(Volume flow rate)と言います。
管内に流れる流体を考えたとき、管の断面積をA(m^2)とおくと体積流量Qv(m^3/s)は下式になります。
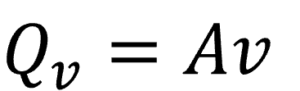
一般に流量というと体積流量のことを指していることが多いと思います。
単位時間あたりに流れる流体の質量を質量流量(Mass flow rate)と言います。
質量流量をQm(kg/s)と置くと下式になります。

連続の式とは

保存されるものの身近な例
連続の式に入る前に保存則のイメージを掴むためにお金の流れを例題として考えてみましょう。
利息がついたり盗まれたりしない限り、収入、支出、貯金の関係は下図のようになります。


簡単ですね!実は連続の式も主張していることはこちらと変わりはありません。
連続の式
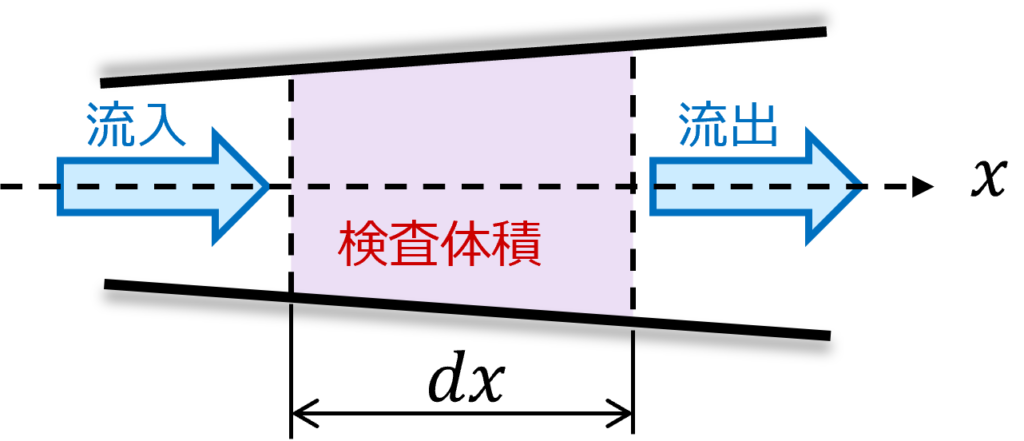
次は管内に流れる流体について考えてみましょう。
流体力学ではある領域の質量流量などを考える際に検査体積(Control volume)という仮想の体積(容積)を考えます。
今回もこのアイディアを用いて考えます。上記と同様に流入質量、流出質量、検査体積内の質量変化は下図のようになります。


これを数学的に表してみましょう。
まず流入質量を求めます。質量(kg)は質量流量(kg/s)に時間dt(s)をかけたものとなるため

となります。次に流出質量を求めます。
流出質量はdxだけ離れていることによる流入質量からの変化量を考慮する必要があります。
ここで流れ方向(x軸方向)の質量の変化率はxで偏微分すればよいため
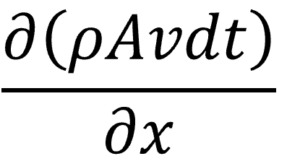
となります。この変化率にdxをかければ流入質量からの変化量となります。
よって流出質量は流入質量に流入質量からの変化量を足して

となります。
偏微分を忘れちゃった人はこの記事を見てね。
よって、流入質量と流出質量の差は下式となります。

次に検査体積内の質量変化に関して考えます。まず、検査体積の流体の質量は下式となります。

いま、検査体積自体は時間により変化しないため、流入と流出に差があれば密度が時間変化します。
また、流れに対して断面積が一定ではないため、密度と断面積を時間で偏微分します。
こちらは単位時間あたりの密度変化を表しているため、さらに時間dt(s)をかけると検査体積内の質量変化量となります。

よって、最初の式にそれぞれ代入すると
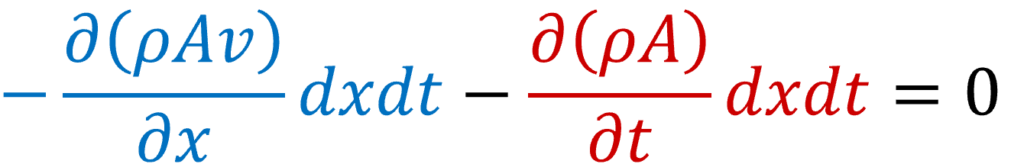
となり、両辺を-dxdtで割ると

となります。ここで断面Aが一定であるとしAで割ると

となり、さらに3次元に拡張しベクトルの方程式で書くと
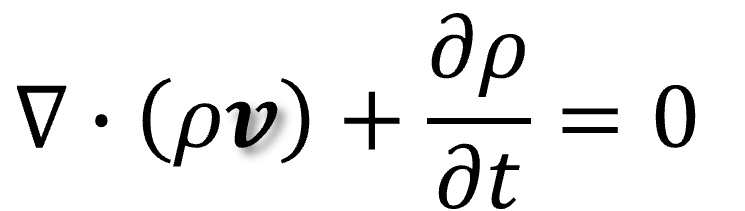
となります。非圧縮性流体(密度が変化しない流体)の場合はさらに簡略化されて
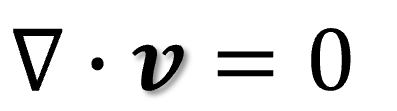
となります。
さいごに
以上で流体力学で用いられる物理法則(保存則)の一つが理解できたかと思います。
もう一つの保存則(ナビエ・ストークス方程式)も理解できれば熱流体解析ソフトで何をやっているのか分からないという不安は大きく減らせるかと思います。
CAEで計算するときは最低限、各保存則が満たされているかくらいは確認しましょう。
また、MATLAB/Simulinkなどの1D CAEソフトでイチからモデルを作る際も基礎となる考え方ですのでマスターするようにしましょう。
さいごに流体力学についてもっと学習したい人に向けておすすめ書籍を載せておきます。





