線接触・面接触の接触面圧を求めよう！【ヘルツの接触理論】

こんにちは、カヲルです！

接触部の摩耗量などを推定する際に固体同士の接触部の面圧を計算したいときってありますよね？

本記事では、ギヤの歯面同士の接触やボールベアリングのボール（転動体）と転送面の接触などに応用されるヘルツの接触理論（Hertz contact theory）について書きたいと思います。

固体同士の接触

荷重がかかる前の固体同士の接触は大きく分けて面接触、線接触と点接触の３つがあります。

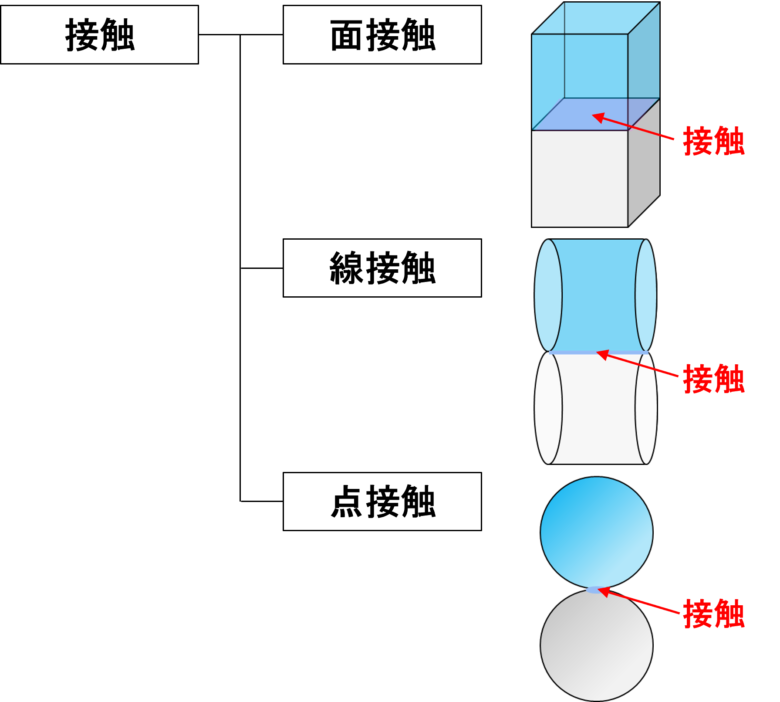
面接触の場合は形状から接触面積が明らかであるため計算に困りませんが、線接触と点接触では面積がゼロであるため通常は接触面圧（contact pressure）を求められません。

しかし、これは荷重がかかる前の場合であり、荷重がかかると弾性変形し微小な接触面が形成されます。これを弾性接触といいます。

弾性変形とは両方の接触物体の荷重を除荷した際に回復する場合を指します。回復しない場合は塑性変形といい今回は対象外とします。

ヘルツの接触理論

ヘルツの接触理論とはヘルツが1881年に円柱面同士、球面同士や任意の曲面同士の弾性接触における理論解をまとめた理論となります。

この理論には下記の前提条件があります。

接触する固体は等質等方性弾性体であること。
接触域は固体の大きさに対して微小であること。
荷重は接触域に対して垂直に作用すること。すなわち接触する表面に摩擦がなく、粗さのない滑らかな表面であること。
変形は弾性限度内であること。

本記事では実用上よく用いられる円柱面同士、球面同士の接触について扱いたいと思います。

なお、平面は半径が無限大の曲面であることから円柱面と平面、球面と平面も含みます。

球面同士の接触

いま下図のように球面同士の接触があるとします。

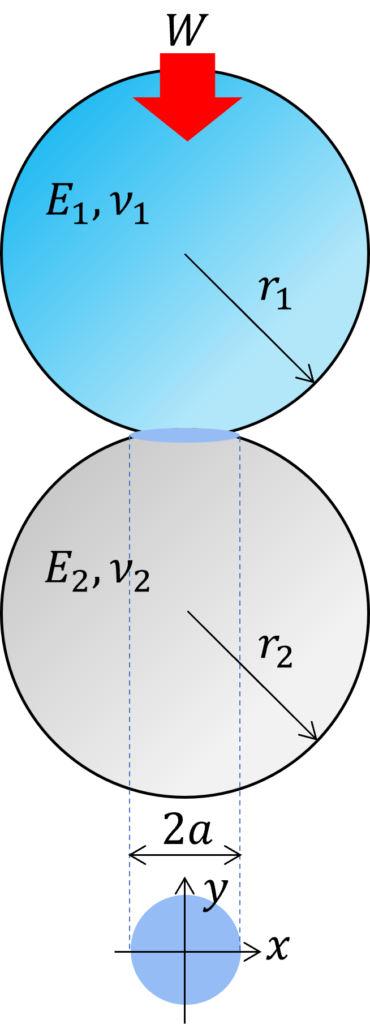
２つの弾性体の曲率半径がr1, r2、ヤング率がE1, E2、ポアソン比がν1, ν2であるとき接触域に対して垂直に荷重Wが印加されると接触域の形状は半径aの円形になります。

この半径aは下式より求めることが出来ます。

$$a = \left( \frac{3WR}{2E’} \right)^{\frac{1}{3}} $$

ここでE’は等価ヤング率（reduced Young’s modulus）、Rは等価曲率半径（reduced radius of curvature）といいます。

等価曲率半径は2つの曲面同士の接触を平面と曲面の接触に置き換えた際の曲面側の曲率半径を表すものとなります。

まず等価ヤング率E’は下式より求まり

$$\frac{1}{E’} = \frac{1}{2} \left( \frac{1 – \nu_1^2}{E_1} + \frac{1 – \nu_2^2}{E_2} \right) $$

変形すると

$$E’ = \frac{2 E_1 E_2}{E_2 (1- \nu_1^2) + E_1(1-\nu_2^2)} $$

となります。また、等価曲率半径Rは下式より求まります。

$$R = \frac{r_1 r_2}{r_1 + r_2} $$

上記で求めた接触域の半径aより平均接触面圧 Pmeanが求まります。

$$P_{mean} = \frac{W}{\pi a^2} $$

ヘルツの接触理論では接触域の中央（右図のxy座標原点）で面圧最大となり、そこから放物線状に面圧が分布します。

よって、放物線の性質より最大接触面圧 Pmax（最大ヘルツ圧）は下式となります。

$$P_{max} = 1.5 \, P_{mean} $$

なお、下式を用いると半径a内での任意の位置(x, y)における接触面圧Pを求めることが出来ます。

$$P = P_{max} \sqrt{1 – \left(\frac{x}{a} \right)^{2} – \left(\frac{y}{a} \right)^{2}} $$

また、弾性接触において荷重によって２つの弾性体は相互に接近することが予想されます。

接触域の変形による影響を可能な限り減らすため、接触域から十分離れた位置を基準とした場合の相互の距離の変化量を相対接近量 δといい下式で求められます。

$$\delta = \left( \frac{9W^2}{4E’^2R} \right)^{\frac{1}{3}} $$

球面と平面の接触

前項の特別な場合として下側の弾性体が平面であるときを考えます。

この場合は等価曲率半径に修正を加えます。下側の弾性体の半径をr2→∞と考えればよいため、ロピタルの定理を用いて等価曲率半径は$R=r_1$とすれば計算できます。

円柱面同士の接触

つぎに下図のような円柱面同士の接触を考えます。

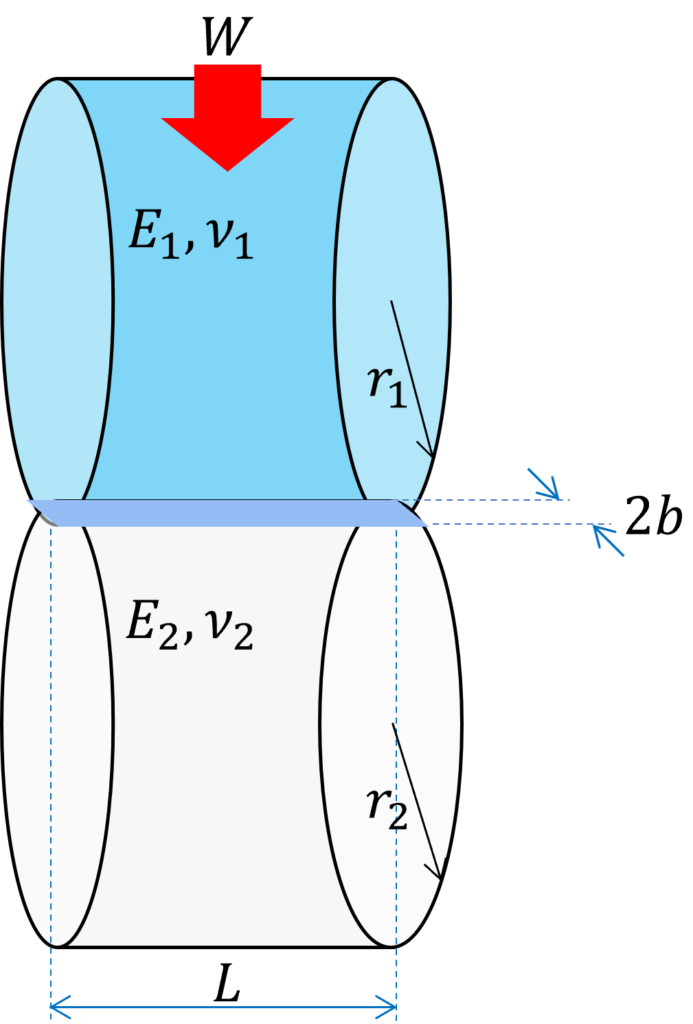
２つの弾性体の曲率半径がr1, r2、ヤング率がE1, E2、ポアソン比がν1, ν2のとき、長さLにわたって均一に荷重Wが印加されると接触域の形状は半幅bの長方形になります。

この半幅bは下式より求めることが出来ます。

$$b = \sqrt{\frac{8R}{\pi E’} \frac{W}{L}} $$

上記で求めた接触域の半幅bより平均接触面圧 Pmeanが求まります。

$$P_{mean} = \frac{W}{2bL} $$

また最大接触面圧 Pmaxは下式となります。

$$P_{max} = \frac{4}{\pi} P_{mean} $$

なお、接触域中央を原点としたときの幅方向の任意の位置xにおける接触面圧 Pは下式にて求めることが出来ます。

$$P = P_{max} \sqrt{1- \left( \frac{x}{b} \right)^2} $$

上式は球面と同様に片方が平面の場合も適用することが出来ます。但し、線接触の場合の相対接近量はヘルツの接触理論では解くことができません。

リンク

まとめ

全ての接触をヘルツの接触理論で解くことはできませんが、接触面圧の算出は難しいので参考になったのではないでしょうか。

今回は球と円柱（平面を含む）の接触について扱いましたが、任意の曲面同士の接触は以下の記事にて紹介していますので差参考にして頂ければと思います。

2022年12月4日任意の曲面同士の接触面圧計算【ヘルツの接触理論】

また、接触面圧を求めたいときは摩擦・摩耗で課題を抱えている場合も多いのではないでしょうか。

摩耗量は摩擦面の温度に依存する場合が多いので、以下の記事にて温度の算出方法を紹介しています。

2022年10月30日摩擦面の温度の計算方法【閃光温度】

摩擦・摩耗を取り扱う分野をトライボロジーと言いますが、体系的に学ぶには書籍での学習が近道です。

「はじめてのトライボロジー」はタイトルの通り、初学者にも配慮された読みやすい構成となっていますが、応用まで含めた実務にも役立つ一冊です。また、演習問題も解説も式の省略も少なく理解しやすくなっています。

はじめてのトライボロジー

リンク

内容（Amazon商品ページより）

基礎から応用までが、この1冊でわかる!
・今をときめく研究者が贈る教科書なので、向かうところ敵なしのわかりやすさです!
・実務に出ても役に立つ知識と考え方を身につけよう!
・表面分析、表面改質、トライボマテリアル、ナノトライボロジーについても詳しく解説。

オーム社の「トライボロジー」は上で紹介した本が物足りなくなった場合に読むことをおすすめします。数式は少し増えますが、基本に忠実に学びたいかたはこちらの本がよいかと思います。

山本雄二(著), 兼田〓宏(著)　トライボロジー

リンク

内容（「BOOK」データベースより）

「トライボロジー」とは、摩擦・摩耗・潤滑など、機械の表面現象に関連した諸問題を取り扱う学問分野である。本書は、機械システムの設計に必要不可欠な、この「トライボロジー」を中心に、関連する知識を体系的にまとめたものである。今回、初版刊行から10年という節目を好機として全編を見直し、必要な訂正を施し「第2版」とした。

物性表【付録】

最後に参考までに各工業材料の物性表を記載したいと思います。

材料名	ヤング率 (GPa)	ポアソン比 –	線膨張係数 (×10^-6/K)	比重 –
SUJ2	207	0.30	12.5	7.83
SPCC	211	0.30	11.7	7.86
S25C	206	0.28	11.8	7.84
S45C	207	0.30	12.8	7.83
SUS303	193	0.29	17.3	8.03
SUS304	193	0.29	16.3	7.93
SUS420J2	200	0.27	10.4	7.75
SUS430	200	0.27	10.4	7.70
A2017	73	0.33	23.6	2.79
A5056	72	0.30	24.3	2.64
ADC12	71	0.28	21.0	2.73
ADC14	81	0.28	19.0	2.70
C2600	110	0.33	19.9	8.53
C3604	96	0.32	20.5	8.50
POM	3.4	0.35	–	1.42
PA6-GF30	7.3	0.35	–	1.36
PA66-GF30	8.0	0.35	–	1.36
PBT-GF30	9.5	0.38	–	1.53
PPS-GF40	13.0	0.37	–	1.66