めねじにボルトをねじ込み回転させると、対象の部品にボルト頭が着座して軸力(Axial force)が発生します。
このとき、ボルトに加えるトルクと軸力との関係は「斜面の原理」を応用して導くことができます。
斜面の原理とは斜面の上に荷物を移動するとき、荷物に加える水平方向の力と荷物の重さとの関係を表す原理をいいます。

これを用いると、小さな水平方向の力で重い荷物を持ち上げることができます。
ここで、傾斜角\(\beta\)(単位:\(^{\circ}\))の斜面に置いた荷物について考えます。
荷物に働く重力を\(F\)(単位:\(N\))と置くと、斜面に垂直な力\(R\)と斜面に平行に力\(S\)に分解することができます。

同様に、荷物を水平に押す力を\(U\)(単位:\(N\))と置くと、斜面に垂直な力\(W\)と斜面に平行に力\(T\)に分解することができます。
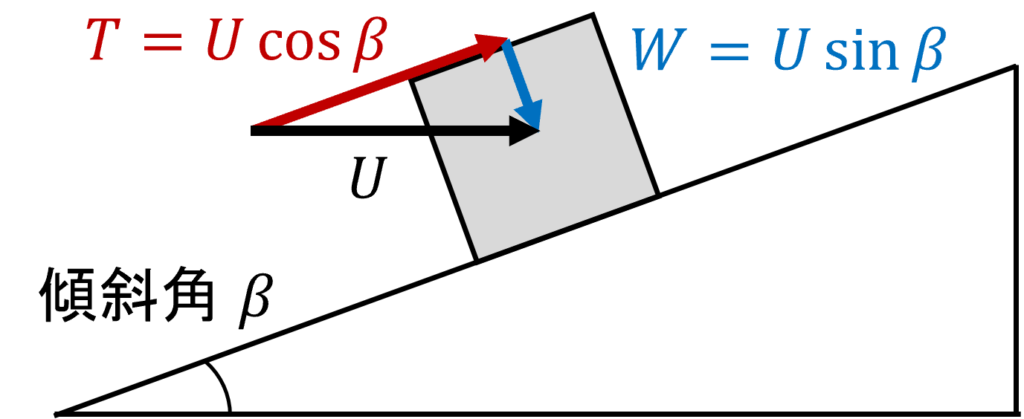
ここで、荷物の底面と斜面との間の摩擦係数を\(\mu\)、垂直抗力を\(N\)(単位:\(N\))と置くと、摩擦力\(M\)(単位:\(N\))は以下のようになります。
また、斜面に平行な力は力のつり合いにより、以下の式が成立します。
式(3)に式(2)を代入し、\(T=U \cos \beta\)、\(S=F \sin \beta\)、\(R=F \cos \beta\)、\(W=U\sin \beta\) を代入すると、
式(7)を\(\cos\beta\)で割り、三角関数の性質(\(\tan\beta = \sin\beta / \cos\beta\))を用いて整理すると、
摩擦角を\(\rho\)(単位:\(^{\circ}\))と置くと\(\tan\rho = \mu = M/N\)の関係にあるので、
となります。また、斜面を下る方向に移動するときは、傾斜角\(\beta\)の符号が逆となるので以下のようになります。

摩擦力\(M\)と垂直応力\(N\)の関係を求めると以下のようになりますね。
- 斜面を上る方向に移動するとき
\(M=F \left[\displaystyle \frac{\sin\rho}{\cos\left(\beta+\rho\right)} \right] \tag{12}\)
\(N=F \left[\displaystyle \frac{\cos\rho}{\cos\left(\beta+\rho\right)} \right] \tag{13}\) - 斜面を下る方向に移動するとき
\(M=F \left[\displaystyle \frac{\sin\rho}{\cos\left(-\,\beta+\rho\right)} \right] \tag{14}\)
\(N=F \left[\displaystyle \frac{\cos\rho}{\cos\left(-\,\beta+\rho\right)} \right] \tag{15}\)
次回は斜面の原理を応用して、締め付けトルクと軸力の関係について見ていくよ!



