【サイレンサの設計】透過音の計算法＜遮音, 質量則＞

エンジンやポンプなどの流体機械は排気騒音（排気脈動）が発生するため、それを低減させるためにサイレンサ（消音器）が設置されます。

サイレンサを設計する上で重要なポイントは拡張室や絞りですが、そちらの設計方法については以下の記事で紹介しました。

2022年9月19日 サイレンサー（消音器）の簡易設計法と勘所【商品性向上】

しかし、拡張室や絞りをいくら上手く設計しても、サイレンサそのものから音が漏れてしまっては意味がありません。

本記事では、サイレンサなどの壁から外に漏れる（伝わる）音の計算方法について解説します。

透過音の計算方法

下図に示す通り、サイレンサの壁（外板）などに音が到達すると壁により反射・吸収が行われますが、一部は透過し音漏れが発生します。これを透過音（Transmitted sound）と言います。

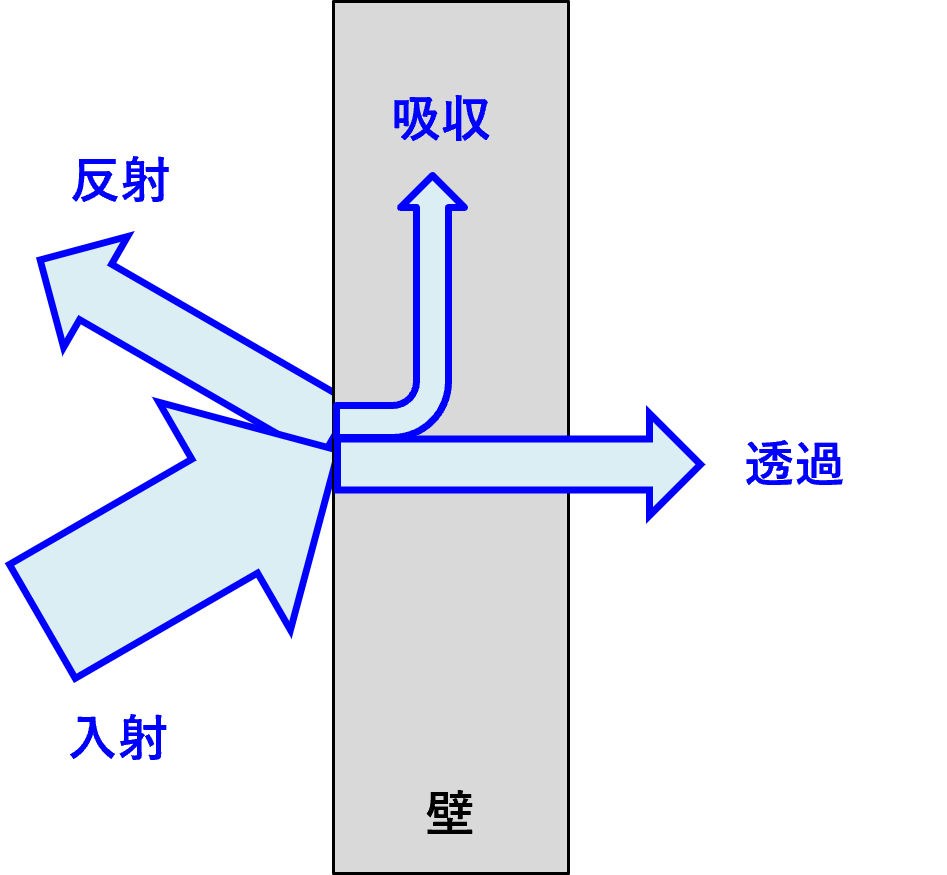
壁を透過する音は空気と壁のもつ音響インピーダンスの比によって決まります。

カヲル

音響インピーダンスに関しては以下の記事を参考にしてね。

2022年10月12日 音とはなにか【音圧レベル、音響パワーレベル】

ここで、空気の密度を\(\rho \, (kg/m^3)\)、空気中の音速を\(c \, (m/s)\)、壁の密度を\(\rho_w \, (kg/m^3)\)、壁の中での音速を\(c_w \, (m/s)\)、壁の厚さを\(l \, (m)\)とおくと、透過率\(\tau\)は下式で求められます。

なお、\(\rho c\)は空気のインピーダンス、\(k = 2 \pi / \lambda \)となります。

一般に壁の厚さは音の波長に対して十分薄いため、角振動数を\(\omega \, (rad/s)\)、壁の単位面積あたりの質量を\(M\) （\(= \rho_w l\)）とおくと、式（１）は以下のように簡略化されます。

カヲル

周波数を\(f \, (Hz)\)とおくと、角振動数は\(\omega = 2 \pi f\)となるよ。

よって、透過損失\({TL}_0 \, (dB)\)は、

となります。式（３）より単位面積あたりの質量が大きくなるほど透過損失が大きくなりますが、この性質は質量則（Mass law）と呼ばれています。

式（３）に実際の空気の密度と音速を代入すると下式のようになります。

なお、\({TL}_0\)は音が垂直に壁に入射したときの透過損失であり、垂直入射透過損失と呼ばれます。壁に対してランダムな角度から入射した場合はランダム入射透過損失\({TL} \, (dB)\)と呼び、下式で求められます。

まとめ

本記事では、透過音の計算方法について紹介しました。

特にエンジンのサイレンサの外板やエキパイなどは厚い金属板で作られることが多いですが、透過音を小さくするために単位面積あたりの質量を大きくする必要があることから、そのような設計になっています。

今回は透過音の計算方法について触れましたが、理論についてもう少し学ばれたい方は以下の書籍などがおすすめです。