近年、カーボンニュートラルなどが叫ばれ、機械に求められるエネルギー効率もますます重要な要素となってきました。
本記事では流体機械の一つであるポンプを設計 又は 選定するときなどにポンプ効率(熱効率)を求める方法について解説します。
なお、流体機械は熱力学を基礎としてますので、もし熱力学を復習されたい方はこちらも記事も併せてご覧ください。
ポンプ効率の求め方
本記事ではポンプの入口(吸気側)と出口(排気側)に圧力計と体積流量計を接続し、実測値からポンプ効率を計算する方法について解説します。
ポンプ効率の測定準備
気体を対象とするポンプの効率を測定する場合は、以下2つを用意します。
- 圧力計(2つ)
圧力計には大気圧からの差分を測る相対圧計と絶対真空からの圧力を測る絶対圧計の二種類があります。
流体機械の圧力を測る際は絶対圧計を用意するようにします。 - 体積流量計(1つ)
流量計には単位時間あたり流れる体積を測る体積流量計と単位時間あたり流れる気体の質量を測る質量流量計があります。
流体機械の流量を測る際は体積流量計を用意するようにします。
もし、相対圧計しかない場合は、大気圧が分かれば絶対圧へ換算することができます。
大気圧(Atmospheric pressure)を\(p_{atm}\)、相対圧(Gauge pressure)を\(p_g\)、絶対圧(Absolute pressure)を\(p_{abs}\)とおくと、絶対圧は下式にて求まります。
なお、圧力の単位は\(Pa\)(パスカル)を用い、計算する際には\(k\)(キロ)など補助単位も外します。
絶対圧計がある場合はなるべく絶対圧計を使おう。
体積流量は基準圧力(例えば101,325 Pa)、基準温度(例えば20℃)時の体積へ換算したノルマル流量と言う表示方法もあります。具体的な基準圧力、基準温度の数値に関しては体積流量計の取り扱い説明書を確認するようにします。
ただし、効率計算には測定時の圧力、温度のままの実流量を用います。

質量流量センサーを用いたものは、ノルマル流量で表示しているものもありますね。
測定誤差が増えるのでおすすめはしないけど、圧力計と温度計を取り付ければ、実流量にも換算できるよ。
基準圧力を\(p_{std}\)、基準温度を\(T_{std}\)、体積流量計内部(または近傍)の圧力を\(p_{line}\)、温度を\(T_{line}\)、ノルマル流量を\(\dot{V}_n\)、実流量を\(\dot{V}_a\)とおくと、実流量は下式にて求まります。
なお、体積流量の単位は\(m^3/s\)、温度の単位は\(K\)(ケルビン)を用います。
ポンプ効率の測定実施
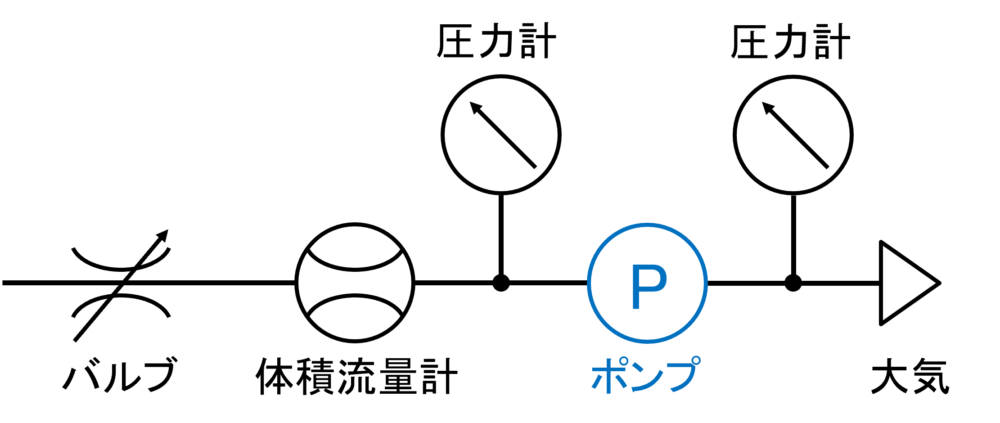
ポンプ効率を測定する際には、下図のように体積流量計と圧力計を接続します。
圧力を固定したいときもバルブで流量を調整することで調整しましょう。
また、測定の際は必ず定常状態になるようしましょう。
本記事で紹介するポンプ効率の計算は途中でリークが発生しないこと(外と物質交換なし)を前提とした式になるので、リークが発生しないように接続してね。

ポンプを外部からモータで動かすなどして、ポンプとモータの間に回転計とトルク計を入れて測定する必要もありますね。
ポンプ効率の計算
まず、定常状態において、ポンプが気体へ与えた単位時間あたりのエネルギー(仕事率)を計算します。
ポンプの吸気側圧力を\(p_{in}\)、ポンプの吸気側実流量を\(\dot{V}_{in}\)、ポンプの排気側圧力を\(p_{out}\)、比熱比を\(\kappa\)とおくと、ポンプから気体が受けた仕事率\(\dot{E}_{out}\)は下式より求まります。
(空気の比熱比は約1.4となります。)
なお、式(3)はポンプの吸気口から排気口へ向けて気体が断熱変化した場合を仮定しています。
もし、等温変化を仮定する場合は下式を用います。
次にポンプへ単位時間あたりに入力されたエネルギー(仕事率)を計算します。
回転速度を\(N\)、角速度を\(\omega\)、トルクを\(\tau\)とおくと、ポンプが受けた仕事率\(\dot{E}_{in}\)は下式より求まります。
なお、回転速度の単位は\(rpm\)、角速度の単位は\(rad/s\)、トルクの単位は\(N \cdot m\)を用います。
以上より、ポンプ効率\(\eta\)は下式より求まります。
効率の計算に式(3)を用いた場合は断熱効率、式(4)を用いた場合は等温効率と言うよ!
まとめ
本記事では実際に体積流量、圧力、回転速度、トルクを測定し、ポンプ効率(熱効率)を求める方法について解説しました。
もし、ポンプについて詳しく学ばれたい方は、以下の本などが参考になるかと思います。
もし、真空ポンプに関して検討している場合は、以下の記事にて性能計算の仕方を解説していますので、併せて読んでみてください。
また、ポンプに関してはNV(音、振動)も大きな関心事項の一つです。
以下の記事も参考して見ては如何でしょうか。









