圧入荷重・スリップトルクの計算法と式の導出

部品間を固定する手段として、圧入（Press fit）は安価でポピュラーな方法の一つです。

正確な圧入荷重の計算は応力ひずみ線図から材料の非線形性を考慮した構造解析（CAE）が必要ですが、初期の設計検討には本記事で紹介する計算式がよく用いられます。

また、圧入設備を導入するときのプレス機の能力選定（見積）にも使われています。

圧入荷重・スリップトルクの計算

本項では圧入荷重、スリップトルクの実際の計算方法について順を追って解説します。

式の導出などは本項後ろの理論編に記載していますので、気になる方はそちらをご覧ください。

圧入代

下図のように、ボス（外筒）にシャフト（内筒）を圧入する場合は、必ずボスの内径に対してシャフトの外径を大きくします。

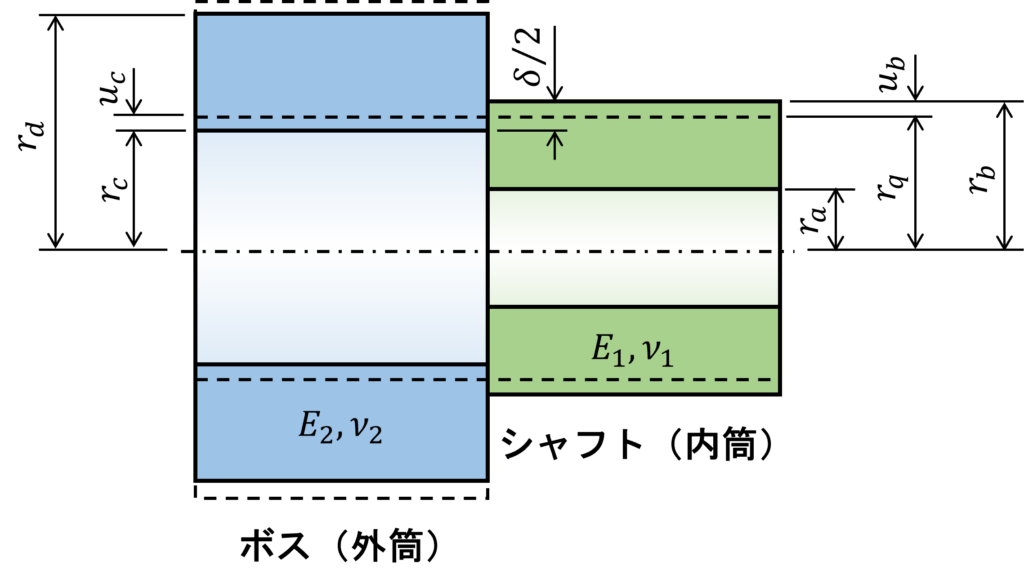
このわずかに大きくした寸法を圧入代と言います。

圧入代$\delta$は下式で計算されます。

$$ \delta = 2 \, ( r_b \, – \, r_c ) \tag{1} $$

カヲル

機械設計での寸法の単位は通常は$mm$が使われるけど、計算時には補助単位を外して$m$を使用してね。

圧入部面圧

圧入は圧入代を設けることにより、弾性変形し圧入部に面圧が発生します。この面圧により圧入は機械的な接合を得ます。

ここで、シャフトの縦弾性係数を$E_1$、ポアソン比を$\nu_1$、ボスの縦弾性係数を$E_2$、ポアソン比を$\nu_2$とすると、圧入部面圧$q$は下式で計算されます。

$$ q = \frac{\delta}{2\,r_b} \left\{ \frac{1}{E_1} \left( \frac{r_a^2+r_b^2}{r_b^2-r_a^2} \, – \, \nu_1 \right) + \frac{1}{E_2} \left( \frac{r_b^2+r_d^2}{r_d^2-r_b^2} + \nu_2 \right) \right\}^{-1} \tag{2} $$

カヲル

縦弾性係数と圧入部面圧の単位は$Pa$（パスカル）となるよ。ポアソン比は無次元量なので単位はないよ。

式（２）はシャフトが中空のものを想定しています。中実のときは$r_a = 0$と置くことにより、下式で計算することができます。

$$ q = \frac{\delta}{2\,r_b} \left\{ \frac{1\,-\,\nu_1}{E_1} + \frac{1}{E_2} \left( \frac{r_b^2+r_d^2}{r_d^2-r_b^2} + \nu_2 \right) \right\}^{-1} \tag{3} $$

圧入荷重（抜け荷重）

圧入荷重$F$は摩擦係数$\mu$と圧入部面積$A$と圧入部面圧$q$の積となります。

圧入長さを$l$とおくと圧入荷重は下式で計算できます。

$$\begin{eqnarray} F &=& \mu \, A \, q \\ \\ &=& 2 \pi \,\mu \, r_b \, l \, q \tag{4} \end{eqnarray}$$

摩擦係数は材料の組み合わせや表面粗さなどによって異なりますが、金属同士の圧入ではおおよそ0.1程度になります。

カヲル

圧入荷重の単位は$N$（ニュートン）となるよ。

スリップトルク（回りトルク）

ボス～シャフト間の回転方向の抵抗力であるスリップトルク$\tau$は下式で計算できます。

$$ \tau = F \, r_b \tag{5} $$

カヲル

スリップトルクの単位は$N \cdot m$となるよ。

設計時の注意点

圧入部品の設計時の注意点はいろいろありますが、代表的なものを記載します。

表面粗さ
ボス側、シャフト側双方とも圧入面の表面粗さの図面指示は必ず入れる様にします。

多くの場合は、Ra1.6以下にすることが多いかと思います。
寸法公差
圧入代はμmオーダーとなることが多いです。そのため、寸法公差は必ず図面指示します。

あまり独自の公差にすると、刃物が特殊になる場合もありますのでJIS（日本産業規格）を参考に設定します。

参考HP）はめあい選択の基礎/寸法公差及びはめあい
幾何公差
圧入部の真円度（円筒度）が低いと有効な圧入代が減少し、圧入荷重やスリップトルクが減少します。

特に海外製作品などは、幾何公差は必ず図面指示するようにしましょう。
線膨張係数
ボス（外筒）とシャフト（内筒）は温度が印加されることで、圧入代が線膨張係数分だけ変化します。

線膨張係数を考慮して圧入代を設定することが重要ですが、可能な限り、線膨張係数が近い材料の組み合わせとなるようにしましょう。
圧入時の傷防止
シャフトへ圧入する部品（外筒）をシャフトの奥のほうで圧入する場合は、シャフト先端から奥まで引きずりながら圧入することになります。

引きずりながら圧入すると、圧入する時間が増え製造コストがあがったり、引きずったところに傷がついたり好ましくありません。

シャフト先端側は１段外径を小さくするなど、なるべくひきずりながら圧入することがないよう設計しましょう。
荷重印加部・荷重受け部の確保
荷重印加部や荷重受け部がない形状だと特殊な治具が必要になったり、安定的に圧入できなくなったりします。

設計段階で製造時にどのように圧入するか考えて形状を決めましょう。

また、製造時には圧入荷重や圧入高さを管理値にするなど、品質を確保するようにしましょう。

物性値表

参考情報として、物性値表を記載します。

材料名	ヤング率 (GPa)	ポアソン比 –	線膨張係数 (×10^-6/K)	比重 –
SUJ2	207	0.30	12.5	7.83
SPCC	211	0.30	11.7	7.86
S25C	206	0.28	11.8	7.84
S45C	207	0.30	12.8	7.83
SUS303	193	0.29	17.3	8.03
SUS304	193	0.29	16.3	7.93
SUS420J2	200	0.27	10.4	7.75
SUS430	200	0.27	10.4	7.70
A2017	73	0.33	23.6	2.79
A5056	72	0.30	24.3	2.64
ADC12	71	0.28	21.0	2.73
ADC14	81	0.28	19.0	2.70
C2600	110	0.33	19.9	8.53
C3604	96	0.32	20.5	8.50
POM	3.4	0.35	–	1.42
PA6-GF30	7.3	0.35	–	1.36
PA66-GF30	8.0	0.35	–	1.36
PBT-GF30	9.5	0.38	–	1.53
PPS-GF40	13.0	0.37	–	1.66

理論編（式の導出）

圧入の計算は材料力学を基礎としており、圧入は厚肉円筒の組み合わせと考えることができます。

内筒の外径$r_b$における変位$u_b$と外筒の内径$r_c$における変位$u_c$は下式で表すことができます。

$$\begin{eqnarray} u_b &=& – \, \frac{1}{E_1} \left( \frac{r_a^2+r_b^2}{r_b^2-r_a^2} \, \, – \, \, \nu_1 \right) r_b \, q \tag{6}\\ \\ u_c &=& + \frac{1}{E_2} \left( \frac{r_c^2+r_d^2}{r_d^2-r_c^2} + \nu_2 \right) r_c \, q \tag{7}\\ \end{eqnarray}$$

圧入代$\delta$は、$\delta / 2= |u_b| + u_c $ の関係にあるので、

$$ \delta = 2 \, q \left\{ \frac{r_b}{E_1} \left( \frac{r_a^2+r_b^2}{r_b^2-r_a^2} \, – \, \nu_1 \right) + \frac{r_c}{E_2} \left( \frac{r_c^2+r_d^2}{r_d^2-r_c^2} + \nu_2 \right) \right\} \tag{8} $$

となります。近似的に$r_b = r_c = r_q$ とおくと下式のようになります。

$$ \delta = 2 \, r_q \, q \left\{ \frac{1}{E_1} \left( \frac{r_a^2+r_q^2}{r_q^2-r_a^2} \, – \, \nu_1 \right) + \frac{1}{E_2} \left( \frac{r_q^2+r_d^2}{r_d^2-r_q^2} + \nu_2 \right) \right\} \tag{9} $$

式（２）は$r_q$に$r_b$を代入し、式を整理したものになります。