こんにちは、カヲルです!
前回は品質管理の基礎知識として工程能力指数について取り上げました。
その中で製品のコストや機能を満たすよう設計するために公差解析を実施することも触れました。
今回は実際に公差解析を行う手順について書きたいと思います。
公差解析とは
公差解析(Tolerance analysis)とは複数の公差が仕様、機能、加工、組立、コストなどを満たすか検証することを言います。
こちらを行うには単品部品の各形状に設定された複数の公差を要素として積み上げ、組立品のばらつきを見積もる必要があります。
この公差を積み上げる(累積する)行為を公差計算(Tolerance calculation)と言い、積み上げた公差を累積公差(Stacked tolerance)と言います。
公差計算方法はあとで紹介するけど代表的ものは下記があるよ。
・ワーストケース(WC:Worst case)
・二乗和平方根(RSS:Root sum squares)
・モンテカルロ法(Monte Carlo method)
・システムモーメント法(Method of system moments)
![]()
公差解析の目的
製品の公差を設定する際には商品性の目標値(品質限界)を決め、それに対して制御不能なノイズなどがあっても機能限界を超えないロバストな設計をする必要があります。
図面の公差上下限でも機能限界を超えないように公差解析を実施して確認する必要があります。
【関連記事】品質限界・機能限界とは
品質管理に必要な工程能力について知ろう!
公差解析の手順
公差計算を実施する上で先ず最初に与える公差は社内や業界の技術標準を参照し対応するものがあればそちらを与えるかと思います。
また、普通公差(一般公差:General tolerance)や普通幾何公差(General geometrical tolerance)で製品の機能を満足できない場合は加工方法や組立方法などを考慮し公差を与えていきますが、設計変更前の一世代古い製品や同一機能の他の製品などの実績値、設計者自身の経験則などから与えることも実際には多いと思います。
後述する公差計算を実施した結果、累積公差が設計上 許容できる累積公差を満たさない場合やコストを満たさない場合は公差の寄与率などを見ながら公差を修正して目標を達成できるように公差再分配(Tolerance reallocation)をしていきます。
普通公差や普通幾何公差は通常は社内規定などで定められているのでそちらを参照しよう。一般的にはJISから引用したものになっていることが多いよ。
【Japanese Industrial Standards:日本産業規格】
・JIS B 0405 普通公差
-第1部:個々に公差の指示がない長さ寸法及び角度寸法に対する公差
・JIS B 0419 普通公差
-第2部:個々に公差の指示がない形体に対する幾何公差
![]()
最も基礎的な公差計算
電気回路の設計では加算・減算以外の公差計算もありますが、機械設計では加算・減算のみで公差計算が済むものが多いように思います。
例題として下図のような3部品で構成される組立品があるものとします。この例題ではそれぞれの部品に公差が与えられており、それらを積み上げてボデーとロッド間のクリアランスの公差を求めるものとします。(この例題では公差計算は加算・減算のみで済みます)
公差計算の手順としてまず下図のようなポンチ絵(公差解析図:Tolerance analysis diagram)を描きましょう。
次に公差計算をする際に分かりやすいように各寸法に番号や記号を振りましょう。下の例では子部品の寸法は小文字の記号、組立品の寸法は大文字の記号を使用しています。
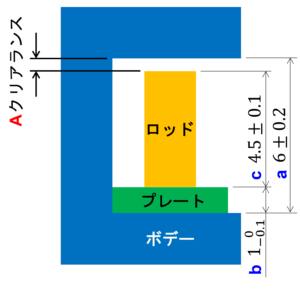
図面をそのまま切り貼りして使うのではなく頭を整理するためにポンチ絵を描くと良いよ。
また、クリアランスのような小さい寸法は実寸大では分かりづらいのでポンチ絵のほうが分かりやすいよ。
![]()
中央値変換
機械図面では例えば穴と軸の嵌め合い公差のように公差の上限(USL)と下限(LSL)が異なる値になっている場合があります。
これを片側公差(変則公差:Unilateral tolerance)と言いますが、公差計算をする際には公差の上限と下限が等しい値である両側公差(Bilateral tolerance)になっている必要があります。
公差計算に使わる寸法が片側公差だった場合、公差域を変えずに両側公差へ変換する行為を中央値変換(Converting dimension to equal bilateral tolerance)と言います。
例として前記のポンチ絵のb寸法は片側公差(1 0 / -0.1)になっています。これを両側公差に変換すると0.95±0.05になります。
ワーストケースによる公差計算
公差計算を実施するにあたり最もシンプルな公差の積み上げ方法は各部品の両側公差の値を全て加算していく方法です。
これは部品寸法が公差範囲内でばらつく最悪な状態を想定して積み上げることになり、全ての部品が最悪の方向で製造されてとしても製品の品質を確保できるため、生産数の少ない製品や治具の設計などでよく使われます。
この方法をワーストケース、最悪状態法や完全互換性の方法などと言います。
実際にワーストケースで累積公差を計算したものを下表に示します。このような表を公差解析表(Tolerance analysis table)と言います。
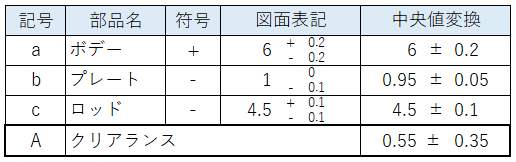
公差を全て加算する際はExcelのSUM関数を使うと簡単だよ!
![]()
二乗和平方根
ワーストケースによる累積公差計算は各部品の公差を全て最悪方向に積んだものになっていましたが、量産工程では通常は公差範囲内に収まるように公差中央を狙って製造・管理(中央値管理)されており、部品寸法の分布も正規分布に従っていることも多いかと思います。
このような条件下で公差の両端(USL, LSL付近)のもの同士が偶然組み合わさる確率は統計的に少ないと考えれるため、これを考慮して公差を積み上げれば累積公差を小さな値にすることができます。
これは分散の加法性(Additivity of variance)を用いた方法になりますが、解析寸法が管理寸法(各部品の寸法)の一次関数で表される必要があります。(公差の積み上げは加算と減算のみである必要がある)
この場合の公差計算方法はまず各寸法の公差を二乗し、それらを全て加算し、平方根(ルート)をとることで求められます。この二乗和平方根による計算方法を不完全互換の方法と言うこともあります。この方法による公差解析表を下に示します。
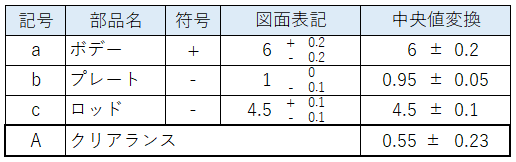
各数値を二乗し、それらの全てを加算する(総和をとる)二乗和の計算はExcelのSUMSQ関数を使うと簡単だよ!
また、平方根の計算はSQRT関数で計算できるので、これらを入れ子構造にするとすぐ計算できるよ!
![]()
掛け算・割り算・関数が含まれる公差計算
前述したとおり、二乗和平方根で累積公差を計算する場合は加算・減算で計算できる場合のみであり、乗算・除算や関数が含まれる場合は累積公差を計算できないものでした。
角度を求めたいときなどは例えば三角関数を使いたい場合があります。このようなときはモンテカルロ法やシステムモーメント法を用います。
モンテカルロ法
一般に寸法などは正規分布に従ったばらつきがあることが多いです。
このばらつきをコンピュータを使って乱数を発生させて再現させ、仮想的に多くの組み合わせを作りそれらの寸法を観察すれば二乗和平方根で計算したときのような統計的な累積公差の計算ができます。但し、コンピュータが作る乱数は一見すると乱数ですが確定的な計算で求められている疑似乱数(Pseudorandom numbers)であり、真の意味で乱数ではありません。
また、モンテカルロ法は手軽であるため公差計算以外にも複雑で一般解を得ることが難しい事象・現象を再現する際のシミュレーションで広く使われておりメリットもありますが、仮想的に作りだした多くの組み合わせから得られる分布はたまたまの産物であり、細かな数字に着目すると再現性がなく、計算時間も長くなりやすいというデメリットがあります。
そのため、実用面で公差計算に使われる例は限られていると思います。
例えばばらつきの分布が正規分布に従い中央値(平均値)が5、標準偏差が1のときの分布をExcelで計算するにはセルに「=NORMINV(RAND(), 5 ,1)」と入力し、オートフィル機能を使って多くの数値を計算し、統計的に処理すれば得られるよ。
![]()
システムモーメント法
モンテカルロ法の再現性がなく、計算時間が長くなりやすいというデメリットを改善するのがシステムモーメント法になります。
システムモーメント法は米国のブリガムヤング大学のKen Chaseh博士によって考案された方法で公差の積み上げを関数として定義し、テイラー展開して解く方法になります。
寸法や角度をx1, x2, …, xiと置き、それらの中央値をμ、公差をTと置くと累積公差は下式で解くことができます。
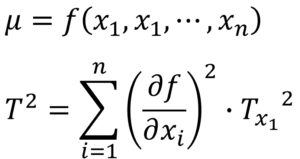
ワーストケースや二乗和平方根での累積公差の例題と同様にポンチ絵を描き、実際に解いてみたいと思います。
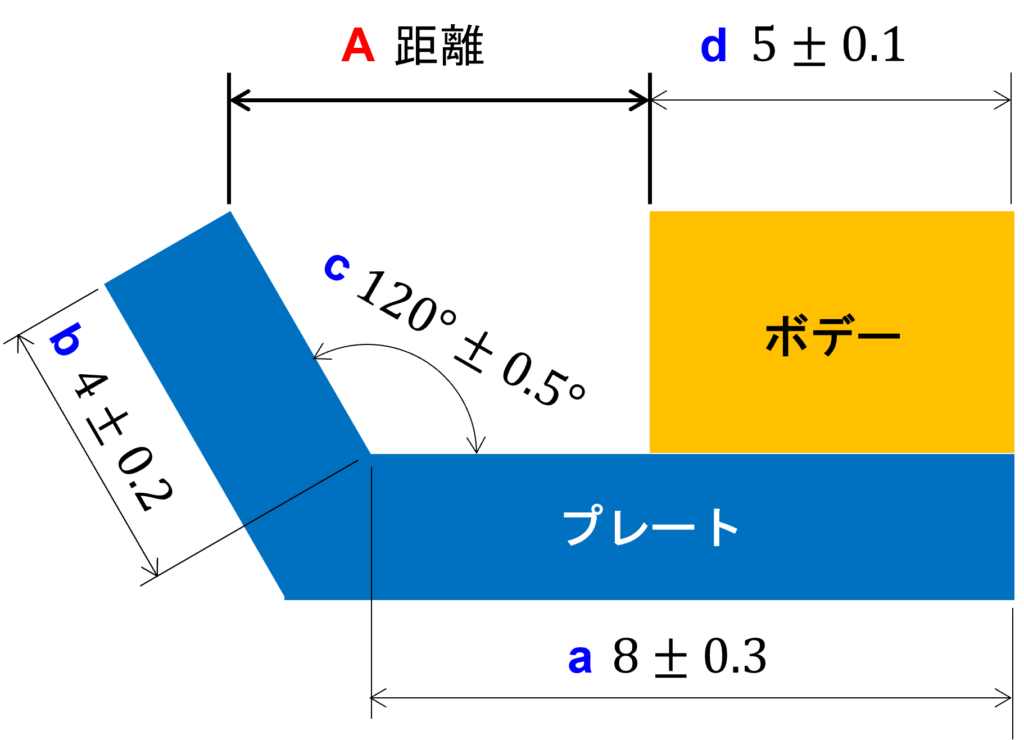
まず、解析寸法の中央値μAを解くために式を立てます。
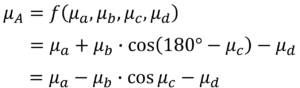
上式に実際の寸法を代入することで中央値が求まります。
![]()
次に上記の式に当てはめ、累積公差を求めます。
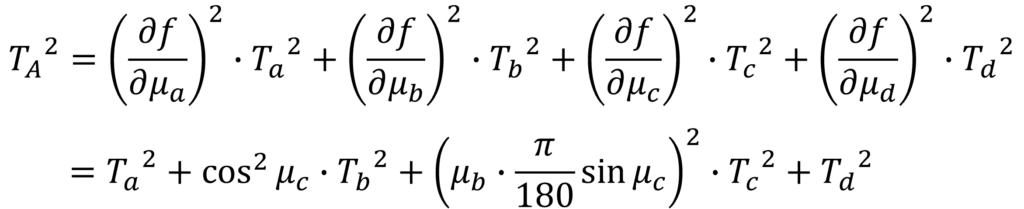
同様に公差の公差の値を代入し、平方根をとり公差を求めます。
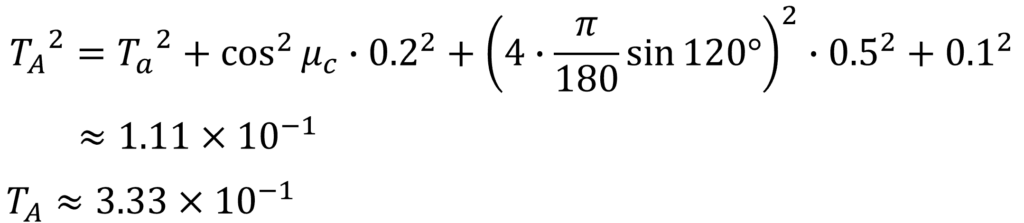
よって累積公差は下記となります。
![]()
まとめ
累積公差の計算はワーストケースと二乗和平方根による方法が基本となりますが、システムモーメント法での求め方を覚えておくと設計の自由度が上がるかと思います。
活用されていなかった方はこれを機会に覚えてみては如何でしょうか。



