心太くんは春から大学生だよね？
そうなんです。
今、線形代数を習ってるんですけど、
難しい割に何に役立つかイメージ湧かなくて。。。
線形代数の実社会での応用例として、
Googleの検索エンジンがあるよ。
まずは、導入として連立方程式を解きながら、
行列について触れてみようか！
今年、理工系の学部に進学された方は数学の必修科目で線形代数（linear algebra）を勉強しているかと思います。
線形代数とはベクトル（vector）や行列（matrix）の性質や相互作用を調べる数学の一分野です。
学年が上がれば連立微分方程式などに応用しますが、心太くんとの会話でもあった通り、本記事では実社会での応用例としてGoogleの検索エンジンを取り上げます。
イントロダクション（まずはExcelで計算してみよう！）
では、実際に連立方程式を行列の形で表し、Microsoft Excelの力を使って解いていきます。
数学の歴史において線形代数は
連立方程式を解く過程の中で生まれた側面があるよ。
実際に手を動かして計算することは、大学の勉強としてとても重要ですが、この部分の説明に関しては多くの良書があります。（記事の末尾で紹介します）
また、最近ではYoutubeなどでも授業や解説などが見れますので、本記事ではそちらに譲りたいと思います。（チート過ぎて怒られそうですが…）
では、先ずはご利益を先にみるために、教育的なもの（中身に相当するもの）は勝手に他人に丸投げしたところで実際に例題に入りたいと思います。笑
例題）鶴と亀が合わせて 40 匹います。足の数を数えたら 86 本でした。
鶴と亀はそれぞれ何匹いるでしょうか？
これは小学校４年生で習う、いわゆる鶴亀算の例題だね！
ここでは小学生のように面積図は書かずにいきなり中学校２年生で習う連立方程式の形で書きます。
この例題は２元連立１次方程式なのでそのままサクッと解けば良いように感じますが、行列を用いて表すと下記になります。
ここで下記のように定義します。
すると下記のように変形できます。
ここで
（エー インバースと読む）は逆行列といい、少々乱暴な言い方をすればスカラーの計算の逆数に相当するものになります。
行列は足し算、引き算、掛け算はあるけど、
割り算はないため、逆行列というものを導入するよ。
また、行列は掛け算の順序で結果が変わるため、の位置は注意してください。
では、パソコンでExcelを開き、下の画面のように入力してください。
先ず、Aの逆行列
を求めます。
E2セルに”=MINVERSE(B2:C3)”と入力し[Enter]を押します。
もし古いExcelを使用されている場合はE2～F3までを選択し、[Ctrl]＋[Shift]＋[Enter]を押してください。
そうすると、逆行列が計算されました。
次にとbをかけてzを求めます。J2セルに”=MMULT(E2:F3,H2:H3)”と入力し[Enter]を押します。
すると下の画面になるかと思います。
するとx = 37, y = 3が得られ、答えは鶴 37羽、亀 3匹になります。
計算自体はコンピュータの力を借りましたが、線形代数を用いることでシステマチックに連立方程式が解けるようになります。
今回は２元連立１次方程式を解いたけど、
同様の操作で１０元だろうが１００元だろうが解くことができるよ！
上記は行列の掛け算と逆行列を求めるのが肝にはなりますが、遠田さんという方のHPで分かりやすく解説されているので紹介します。
- 行列のかけ算のやり方まとめ。
https://atarimae.biz/archives/23930 - 逆行列の求め方。
https://atarimae.biz/archives/24004
線形代数の実社会での応用例
では、実社会での応用例の１つとして
Googleの検索エンジンを見ていこうか！
検索エンジンの歴史
インターネットを使用することでいろいろな情報が得られますが、GAFAMの一角を担っているGoogleが今日では非常に有名です。
現在、日本国内においてGoogleは8割のシュアを持っており、残り2割をYahoo!とbingで分けていますが、Yahoo!はGoogleの検索エンジンを用いており、実質的には9割5分のシュアとなっています。
しかし、現在のシュアから考えると意外に思われる方もいるかもしれませんがGoogleの登場は1997年とかなり後発でした。
既にAltaVista，Excite，Infoseek，Lycos, WebCrawlerなどたくさんのロボット型検索エンジンが登場しており、激しい競争が繰り広げられていました。
この頃の検索エンジンは検索されているキーワードに合致する単語が多く含まれているWebページが上位に表示される仕組みとなっていました。
そのため、実際のWebページの内容とは関係ないキーワードを大量に埋め込んでランキングの上位に表示させるという手口が横行していました。これに対処するためには検索エンジン側でWebページの重要度（質が高いものか）を見極める必要があります。
そこで、スタンフォード大学の大学院生であった ラリー・ペイジ と セルゲイ・ブリン は、検索エンジンのランキングのロジックに「PageRank」という新しいアイディアを提示し、イノベーションを起こしました。参考までにWikipediaよりPageRankの概要を引用したものを記載します。
PageRank 引用元：Wikipedia
PageRank アルゴリズムの発想は、引用に基づく学術論文の評価に似ている。
- 学術論文の重要性を測る指標としては、被引用数がよく使われる。重要な論文はたくさんの人によって引用されるので、被引用数が多くなると考えられる。同様に、注目に値する重要なウェブページはたくさんのページからリンクされると考えられる。
- さらに、被引用数を用いる考え方に加えて、「被引用数の多い論文から引用されている論文は、重要度が高い」とする考え方が以前から存在した。ウェブページの場合も同様に、重要なページからのリンクは価値が高いと考えられる。
- ただし、乱発されたリンクにはあまり価値がないと考えられる。リンク集のように、とにかくたくさんリンクすることを目的としている場合には、リンク先のウェブページに強く注目しているとは言い難い。
この発想を、数億～数十億ページにのぼるウェブページのリンク関係にも適用したのが PageRank である。この方法を適用することにより、仲間内でリンクし合っているだけのサイトの重要度が上がりにくくなり、リンク集のような多くのリンクを張っているだけのサイトからのリンクの重要性を相対的に減らす効果がある。
検索エンジンの仕組み
では、PageRankのアイデアの一片を体験してみようか！
基本的な仕組みはWebページ同士のリンクを行列で表現し、解析することです。
世界のWebページの総数は１８億（！）あるとされますが、ここでは簡単化のために４つのサイトがある場合について考えることにします。下図にサイトのリンク例を示します。
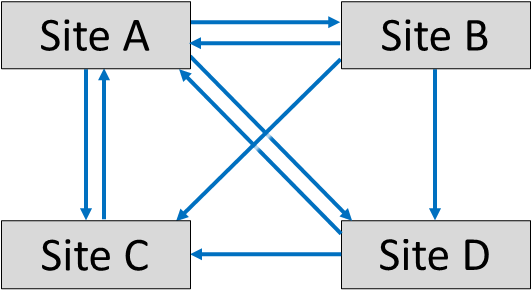
先ず、各サイトから出しているリンクの数をまとめます。
ここで各サイトは固有の得点Piを持っているとします。(iはA～Dが入る）
あるサイトの得点は各サイトの得点を「出しているリンク数」で割ったものの合計とします。
サイトAはサイトB、CとDからリンクを受けています。サイトBが出しているリンク数は3、サイトCが出しているリンク数は1、サイトDが出しているリンク数は2なのでサイトAの得点は下記になります。
この時、リンクを受けていないものがあれば０（ゼロ）とします。
同様にサイトB、C、Dを求めると下の様になる。
この様に各サイトの得点は基本的にはリンクを受けたサイトの合計点となり、被リンクが多いものは重要度が高いとされます。
しかし、この中でリンクを多く出しているサイトは点数が低くなるように重みづけされるため、リンク集などの点数は低くなるように調整されます。
上記４つの式を行列で表現すると下記のようになります。
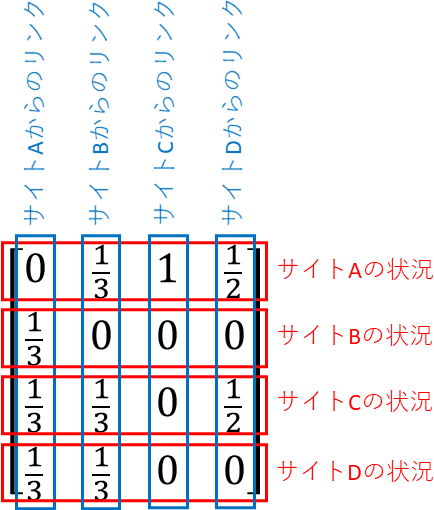
この行列より固有値、固有ベクトルと呼ばれるものを求めるとどのサイトが重要なサイトであるか分かります。
線形代数で出てくる固有値、固有ベクトルの説明はやはり遠田さんのHPが分かりやすいのでそちらに譲りたいと思います。
・固有ベクトル、固有値とはなにか？
ここでは手計算はせずにカシオ計算機の「ke!san」というサイトで求めたいと思います。下のリンクよりサイト開きます。
https://keisan.casio.jp/exec/system/1505174268
次に上で求めた行列を入力し、[計算]ボタンを押します。そうすると固有値λ1 = 1の時のx1, x2, x3, x4が計算され、PA, PB, PC, PDに対応します。
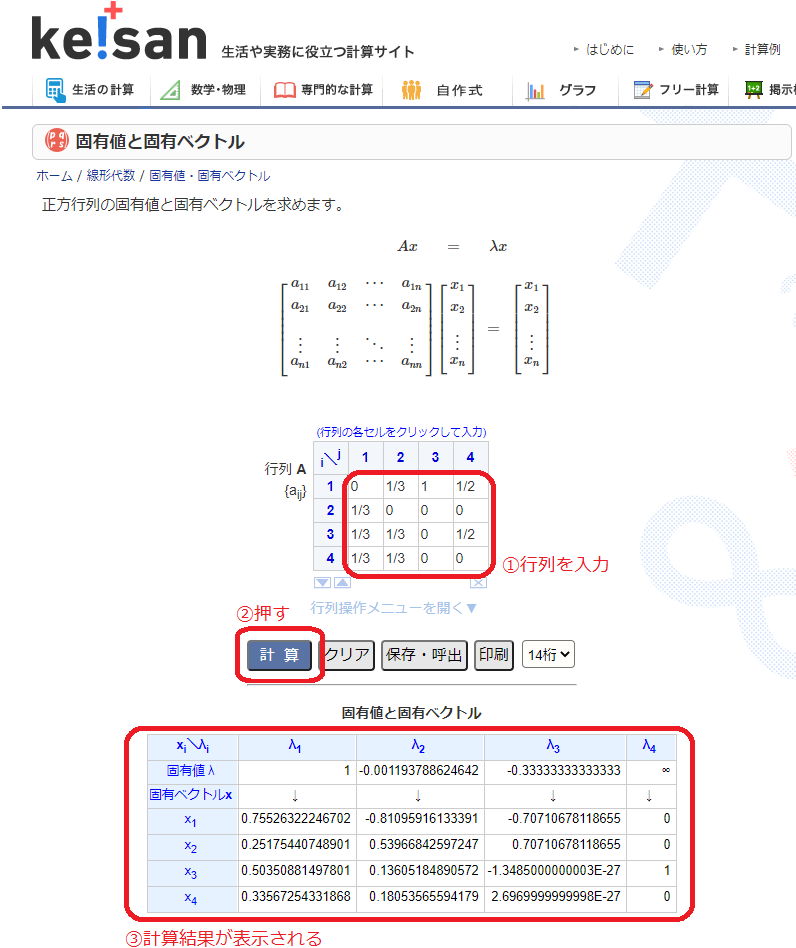
得点はPA > PC > PD > PBとなり、サイトAが一番重要（質が高い）ことが分かります。
【Column】線形代数と人工知能（AI）との関係
線形代数は人工知能にも使用されてるよ。
おまけとして人工知能との関係も説明するね！
人工知能（AI：Artificial Intelligence）とは、人間が普段行うさまざまな思考や判断を人工的に再現したコンピュータシステムのことです。
人工知能を作る（プログラムする）手法として機械学習（ML：Machine learning）があります。
これはコンピュータに大量のデータを与えることで、コンピュータが自動で学習していく手法です。
機械学習の中には、さらにディープラーニング（Deep Learning）という手法があります。
ディープラーニングにはニューラルネットワーク（Neural network）というものが用いられます。
これは人間の脳にあるニューロン（神経細胞）を機械的に再現したものです。
このニューラルネットワークに線形代数が用いられています。
分かりやすく解説！人工知能、機械学習とは
※更新情報（2022年8月4日）：なんと０円コースあります！
機械学習以外の分野でも、ますます需要が高まるプログラミング。
プログラミングスクールのTechAcademyにて１週間の無料体験があるとの情報をゲットしました。無料なのでとりあえず試してみるのもありかも。
社会での活用例（コンピュータ シミュレーション）
理工系大学生の卒業後の進路としてエンジニアの職に就くかたも多いかと思います。
エンジニアとして働くと、製品開発に携わる訳ですが、製品の試作前にはコンピュータによるシミュレーション（CAE解析）を実施して、目標とする性能・品質、耐久性を確保できるか確認を行います。
CAE解析には以下のものがあります。
- 構造解析
構造物や物体に荷重をかけたとき、変形や応力がどの程度発生するのかを計算すること。
強度の検討などに用いられる。 - 機構解析
複数の剛体をジョイント、ギア、バネ、ダンパーなどで接続し、機械として運動する様子を計算すること。
設計したカムやリンクなどの機械要素が想定した通り動くか確認することなどに用いられる。 - 流体解析
空気などの流体の流れや熱の移動などを計算すること。
エンジンやポンプなどの流体機械の性能検証や、放熱性の確認などに用いられる。 - 電磁界解析
対象物の電磁場の相互作用などを計算すること。
モータなどの開発に用いられる。
これらのシミュレーションを使用したり、自分でシミュレーションを行うソフトなどを作成する際に線形代数の知識を用いて計算を行います。
下の記事はモータの応答（動作）をコンピュータ上で再現するモデルの作成例ですが、線形代数の知識が必要不可欠になってきます。
基礎から学ぶDCモータの1Dモデル化① ～MATLAB/Simulink～
まとめ
上記は線形代数の有用性の一片ですが、ただただ計算させられる意味のない数学ではないことは感じて頂けましたでしょうか。
目的が不明だとモチベーションが上がらないと思いますが、勉強を進める上で少しでも役に立ってて頂ければ幸いです。
最後におすすめの書籍を紹介して終わりにしたいと思います。
【参考】線形代数 おすすめ書籍
高校の教科書と違って大学の教科書って急に不親切になるよね。
まずは入門的な本から読むことをおすすめするよ。
出版社からのコメント（Amazonより）
マンガでわかるシリーズはあえて数式をさけていません。ただ数式が苦手な人でも読めるように工夫しています。ぜひ苦手な人もこの分野のエキスパートになれるよう願ってやみません。このシリーズで読者の方の苦手意識が払拭されれば幸いです。
内容（Amazonより）
線形代数は理系学生には分野を問わず必須の科目だが初学者が躓きやすい。
教育系YouTuberヨビノリたくみ氏は、専門書に進む前に挫折する人を多く見てきた先輩として、
「この現状を変えたい」
といった思いから、線形代数入門の連続動画講義を投稿した。
その講義は再生回数200万回を突破し、
「文系でもすごくわかりやすい」「テストでいい点とれた」と好評で、
多くの視聴者の希望も後押しして書籍化に至った。
演習は高校で慣れ親しんだチャート式もあるよ！
内容（Amazonより）
姉妹書『数研講座シリーズ大学教養線形代数の基礎』に掲載された練習,章末問題249問に加え,本書『チャート式シリーズ大学教養線形代数の基礎』にのみ掲載された48問,計297問を,高校数学の参考書“黄チャート”と同様の例題方式で詳解した線形代数の参考書です。
内容（Amazonより）
姉妹書『数研講座シリーズ大学教養線形代数』に掲載された練習,章末問題242問に加え,本書『チャート式シリーズ大学教養線形代数』にのみ掲載された40問,計282問を,高校数学の参考書“青チャート”と同様の例題方式で詳解した線形代数の参考書です。チャート式シリーズの特徴である「その問題を解決するための考え方を示す指針」と,関連する参考事項や注意事項などについても適宜解説を加え,より理解が深まるようにしています。
【参考】線形代数と関連するおすすめ書籍
プログラミングの世界でも線形代数はよく使われているよ！
内容（Amazonより）
ベクトルや行列を扱う線形代数は、CGをはじめとする画像処理プログラミングだけでなく、構造化されたデータを扱うすべての処理の背景となる学問。しかし、抽象的で難解という側面もあり、独学で数学の教科書を紐解くのは困難である。本書は、プログラミングをする人たちに的を絞った構成で、線形代数とそのコンピュータサイエンスにおける応用をわかりやすく説明するもの。
内容（Amazonより）
大人気「10秒で始める人工知能プログラミング学習サービス」の代表者がおくる、
人工知能プログラミングに必要な数学を、やさしく学ぶ参考書が登場!
キホンのキホンからおさらいするから、ニガテな人でも大丈夫!
後半では、Pythonのコードを動かしてさらに理解を深められます!
