【ねじ締結基礎】締め付けトルクから軸力の計算法

前回の記事では、摩擦のある斜面に置かれた荷物を移動させるときに必要な力を求める「斜面の原理」について解説しました。

今回の記事ではねじの締め付けトルクから軸力を計算する方法について解説します。

ねじの軸力とトルクの関係

下図のように、ボルトとめねじが加工された部品で締結された状態について考えます。

ここで、ボルトの頭をトルク$T_f$（単位：$N \cdot m$）で締め付けた際に発生する軸力を$F_s$（単位：$N$）とします。

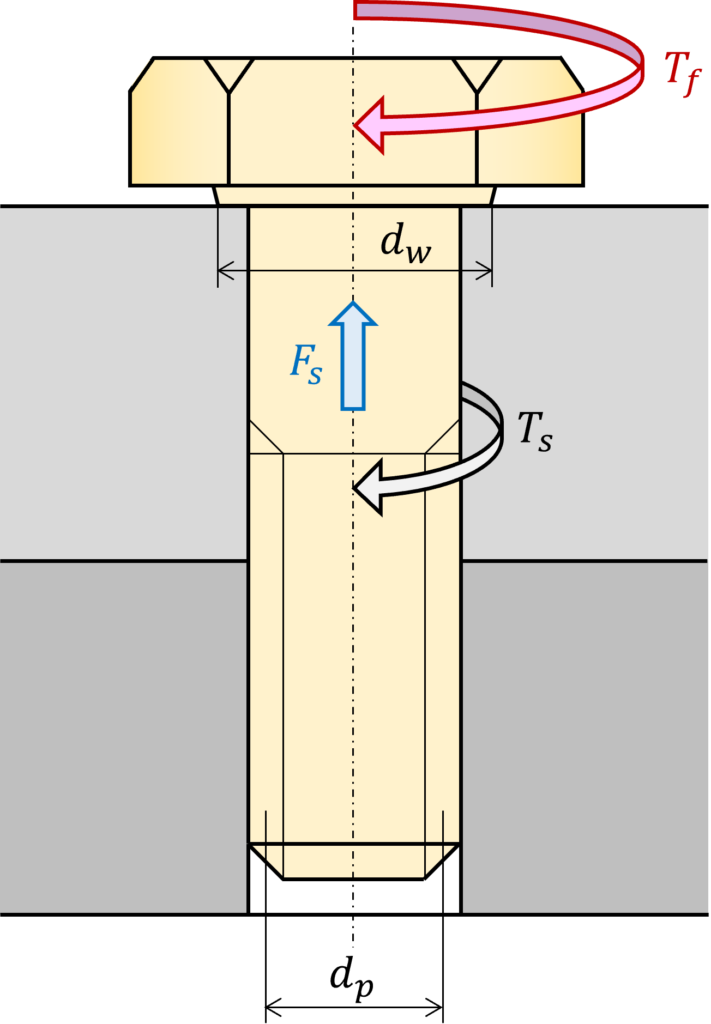
締め付けの際にボルト軸部に発生したトルクを$T_s$（単位：$N \cdot m$）とすると、$T_f$は$T_s$とボルトの頭の座面での摩擦トルクとの和に等しくなります。

よって、ボルトの頭の座面での摩擦係数を$\mu_w$、ボルトの頭の座面での等価摩擦直径を$D_v$（単位：$m$）とすると締め付けトルク$T_f$は以下の関係となります。

$$ T_f = T_s + \frac{D_v}{2}\cdot \mu_w F_s \tag{1} \\ $$

ここで、ボルトの頭の座面直径を$d_w$（単位：$m$）、ボルト穴径を$d_h$（単位：$m$）とすると、等価摩擦直径は下式で計算されます。

$$ D_v = \frac{2}{3} \left(\frac{{d_w}^3 \,-\, {d_h}^3}{{d_w}^2 \,-\, {d_h}^2} \right) \tag{2} \\ $$

前回の記事で解説した斜面の原理を応用し、水平方向の力$U$（単位：$N$）が接線方向に作用していると考え、ねじの有効径を$d_p$（単位：$m$）と置くと、軸部に発生したトルク$T_s$は以下のようになります。

$$ T_s = \frac{d_p}{2} U \tag{3} \\ $$

前回の記事で解説した斜面の原理では斜面の最大傾斜と進行方向が同じでしたが、ねじ山は径方向でも傾斜がついているため、ここでは相当摩擦角$\rho’$（単位：$^{\circ}$）を導入します。

ねじの有効径位置でのリード角を$\beta_p$（単位：$^{\circ}$）と置くと、前回の記事で求めた関係式は以下のようになります。

$$ U = F_s \tan\left(\beta_p+\rho’\right) \tag{4} $$

カヲル

ねじのピッチを$P$（単位：$m$）と置くと、$\beta_p$は以下の関係になるよ！

$\beta_p=\tan^{-1} \left(\displaystyle \frac{P}{\pi d_p} \right) \tag{5} $

さらに、式（３）に式（４）を代入すると、以下のようになります。

$$ T_s = \frac{d_p}{2} F_s \tan\left(\beta_p+\rho’\right) \tag{6} \\ $$

ここで、$\tan \left(\beta_p+\rho’\right) \approx \tan\beta_p+\tan\rho’$と近似し、さらに$\beta$が小さいため$\rho’ \approx \rho$とし、$\alpha = 30^{\circ}$とすると、式（６）は以下のようになります。

$$ T_s \approx \frac{d_p}{2} F_s \left(\tan\beta_p+1.155\mu_s \right) \tag{7} \\ $$

ただし、$\mu_s$はねじ面での摩擦係数とします。

式（７）を式（１）に代入すると締め付けトルク$T_f$が求められます。

締め付けトルク $T_f$

$$ T_f = \frac{1}{2} F_s \left\{d_p\left(\tan \beta_p + 1.155 \mu_s\right) + D_v\mu_w\right\} \tag{8} $$

また、戻しトルク$T_l$に関してはリード角$\beta_p$の符号を逆にすればよいので

締め付けトルク $T_l$

$$ T_l = \frac{1}{2} F_s \left\{d_p\left(-\tan \beta_p + 1.155 \mu_s\right) + D_v\mu_w\right\} \tag{9} $$

となります。軸力から締め付けトルクを求めるには式（８）を$F_s$について解くと求めることができます。