自動車などでの騒音の測定では、無響室(Anechoic room)に測定対象のものを設置し、マイクを使って測定行います。
測定したデータは、騒音の大きさを示す数値として音圧レベル、音響パワーレベルという指標がよく用いられます。
本記事では音の正体について学習し、音圧レベルや音響パワーレベルとはなにかについて理解することを目指します。
- 完全無響室
音が響かないように壁、天井、床に吸音性が高い材料を用いた実験室。 - 半無響室
壁、天井のみに吸音性が高い材料を用いた実験室。
重いものを測定する際などは硬い床になっている半無響室を用いる。
音の基礎知識

音とはなにか
家の中では人の話し声やテレビなど音、家の外では自動車の音や飛行機の音など、日常生活ではあらゆる音に溢れています。
一般的に使われている音(Sound)という言葉は、人間の耳で知覚できるものを言います。
では、音の正体について少しみていこう。
音は真空中では伝わらず、音を伝えるためには必ず気体・液体・固体のいずれかの物質が必要になります。この物質を媒質(Medium)といいます。
私たちがよく耳にしている音は、Fig. 1に示すような空気を媒質した圧力変化の波動になります。このような波を音波(Sound wave)と言います。
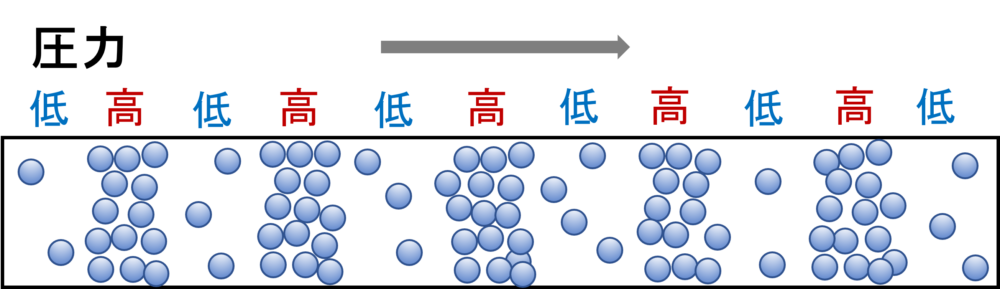
波動の変化の速さを表すものとして、1秒あたりの変化の回数という指標があります。これを周波数または振動数(Frequency)と言い、単位は\(Hz\)(ヘルツ)が用いられます。
人間の耳で知覚できる音波は、年齢によっても異なるけど、20Hzから20,000Hz程度だよ。

人間の耳に聞こえない低い周波数を超低周波(Very low frequency wave)、高い周波数を超音波(Supersonic wave)と言いますね。
また、音が発生する原因は以下のものがあります。
- 媒質の中での物体の振動
楽器やスピーカーから音が聞こえるのは、弦や振動板が振動しているからです。
また、機械から音がするのも機械が振動しているからです。 - 媒質自体の一部で起きる変動
拍手や雷のような、媒質自体が急激に膨張・圧縮、あるいは炸裂する場合などで音が発生します。
送風機、ポンプ、ジェットエンジンなどが同じ原因で音がしています。
なお、音について扱う学問を音響学(Acoustics)と言います。
音圧と粒子速度
ここでは音の物理的な性質について考えてみましょう。
Fig. 2に示すように、圧縮可能な媒質で満たされた半無限長の管を考えます。
管の左端は振動板によって閉じられ、管は十分に細くなっており、軸に垂直な各断面で媒質の物理的な性質は同じものとします。
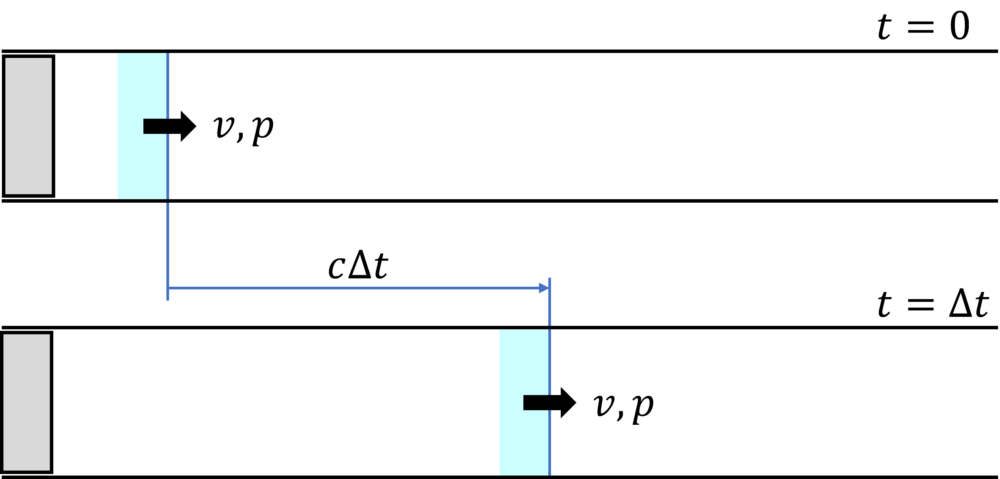
時刻 \(t = 0\) のとき、振動板を右側に急に移動させると、振動板近くの媒質だけ圧縮され、この部分だけ管の中の平均圧力より高くなります。
また反対に、振動板を左側に急に移動させると、振動板の近くの媒質だけ膨張し、この部分だけ平均圧力より低くなります。
振動板が左右に振動すると、圧力が高いところと低いところが繰り返される粗密波が発生し、管の中を伝播します。
このように音波とは、媒質の中を伝播する粗密波を言い、粗密波が伝播する速度を音速(Sound speed)と言います。
Fig. 2は音波が音速\(c \, (m/s)\)で伝播し、\(\Delta t\, (sec)\)後に距離\(c \, \Delta t \, (m)\)だけ進んだことを示しています。
また、平均圧力を基準にして、音波によって起こる圧力の変化分を音圧(Acoustic pressure)と言い、単位は\(Pa\)(パスカル)が用いられます。
また、ある断面に圧力変動が到達すると、媒質を構成する微小粒子は変位させられ、速度を持ちます。この速度を粒子速度(Particle velocity)と言い、単位は\(m/s\)が用いられます。
粒子速度は圧力変動の伝播がきた際に、その位置に元からあった粒子の速度で音速とは別ものだよ!
音響インピーダンス密度
音響インピーダンスは、電気工学におけるインピーダンスの概念を拡張したもので、音圧と媒質の体積速度の比で表されます。
しかし、一般には体積速度の代わりに粒子速度が使われ、音圧と粒子速度の比を音響インピーダンス密度(Acoustic impedance density)と言い、単位は\(Pa \cdot sec/m\)を用います。
音圧を\(p\)、粒子速度を\(v\)と置くと、音響インピーダンス密度\(z\)は下式で表されます。
また、音響インピーダンス密度は、下式より求められます。
上式より、音響インピーダンス密度は媒質に固有な定数値になります。これを特に固有音響インピーダンス(Specific acoustic impedance)と言います。
| 密度 \(\rho\) \((kg/m^3 )\) | 音速 \(c\) \((m/sec)\) | 固有音響インピーダンス \(z\) \((N \cdot sec / m^3)\) | |
|---|---|---|---|
| 空気 \((20 \, ℃)\) | \(1.18\) | \(343\) | \(405\) |
| 水 \((20 \, ℃)\) | \(1,000\) | \(1,500\) | \(1.50 \times 10^6\) |
| コンクリート | \(2,600\) | \(3,100\) | \(8.10 \times 10^6\) |
| 鋼 | \(7,700\) | \(5,000\) | \(3.90 \times 10^7\) |
音圧は電圧、粒子速度は電流に相当するので、固有音響インピーダンスが大きい媒質中では、そうでないものに比べて、同じ粒子速度で音圧は大きくなるよ。

金属のような硬い材料では固有音響インピーダンスが大きくなり、気体では固有音響インピーダンスが小さくなりますね。
音の強さとエネルギー

瞬時値と実効値
音圧\(p\)、粒子速度\(v\)とも一般には時々刻々と正負の値をとって変化します。このときの一瞬一瞬の値を瞬時値(Instantaneous value)と言います。
このような時々刻々と変化する値の大きさを表すのに、平均値(Mean)がまず思い浮かびます。
しかし、音圧は平均圧力を基準とした圧力変動を表す量のため、平均値を用いるとゼロになってしまいます。
よって、二乗して正負の符号を外して平均化した実効値(RMS:Root mean square value)が用いられます。
周期\(T \ (=1/f)\)で音圧が周期的に変化するとき、 音圧\(p\)の実効値\(p_e\)は下式で表されます。
なお、粒子速度\(v\)の実効値\(v_e\)は、式(3)の\(p\)を\(v\)で置き換えたものになります。
瞬時値に関しても、式(1)の関係は成り立つよ!
$$z = \frac{p_e}{v_e} \tag{4} $$
音圧と音圧レベル
日常聞く音の音圧は、実効値にて \(10^{-5} \, Pa\) から \(100 \, Pa\) までの広い範囲の値を取ります。
そのため、音圧の大きさをリニアスケールで扱うと不便なものとなります。
そこで、音圧\(p_e\)と人間の\(1 \, kHz\)での最小可聴値\(p_{e0}\)との比に対して常用対数をとった音圧レベル(Sound pressure level)が用いられます。
音圧レベル\(L_p\)を式で表すと下記となり、単位は\(dB\)(デシベル)となります。
なお、最小可聴値は個人差がありますので、国際規格(ISO 389-7:2005)にて\(20 \times 10^{-5} \, Pa\)と定められています。
人間の聴覚は10dB大きい音を2倍、10dB小さい音を1/2倍と感じるので、logを用いることで人間の感覚に近づけることができるよ。
| 音圧 \(Pa\) | 音圧レベル \(Pa\) | 備考 |
|---|---|---|
| \(2 \times 10^2\) | 140 | ジェットエンジン(3 m) |
| \(2 \times 10^1\) | 120 | 工場内の音 |
| \(2 \times 10^0\) | 100 | オーケストラ(10 m) |
| \(2 \times 10^{-1}\) | 80 | 混雑した街 |
| \(2 \times 10^{-2}\) | 60 | 会話の音 |
| \(2 \times 10^{-3}\) | 40 | 郊外の夜間 |
| \(2 \times 10^{-4}\) | 20 | ささやき声 |
| \(2 \times 10^{-5}\) | 0 | 最小可聴音 |

最小可聴音より小さい音は \(p_e/p_{e0}\) が小数になるので、音圧レベルがマイナスの値になりますね。
音響インテンシティと音響インテンシティレベル
音圧\(p\)と粒子速度\(v\)について扱いましたが、音が発生するときにもエネルギーが必要です。
ここで音のエネルギー(音のなす仕事)について考えてみましょう。
微小な時間\(\Delta t\)の間に粒子は\(v \Delta t\)進むので、単位面積当たりの音のなす仕事\(\Delta E\)は
となります。これを微小時間\(\Delta t\)で割れば、単位時間・単位面積あたりの音のエネルギー\(E\)が求められます。
\(E\)は単位時間・単位面積あたりのエネルギー(仕事)を表しているため、単位はJ/(s・m2)となりますが、単位時間当たりの仕事は仕事率になりますので、単位を整理すると\(J/m^2\)となります。
ここで、エネルギー\(E\)の時間平均\(I\)は、周期的な音に対して
となります。ここで定義された\(I\)を音響インテンシティ(Sound intensity)または音の強さと言い、単位は前記の通り\(W/m^2\)となります。
また、音圧と粒子速度の実効値\(p_e\)、\(v_e\)で表すと
となります。
音響インテンシティは音圧レベルと同様に、通常は常用対数をとった値を用います。これを音響インテンシティレベル(Sound intensity level)または音の強さのレベルと言い、単位は\(dB\)が用いられます。
なお、基準値は\(I_0 = 10^{-12} \, W/m^2\)を取ります。
音響パワーと音響パワーレベル
断面積\(S\)の断面を通して単位時間あたりに伝えられる音のエネルギーは、音響インテンシティ\(I\)に断面積\(S\)を掛けたものとなります。
これを音響パワー(Sound power)と言い、単位は\(W\)(ワット)を用います。
音響パワーも同様に、通常は常用対数を取った値を用います。これを音響パワーレベル(Sound power level)と言い、単位は\(dB\)が用いられます。
なお、基準値は\(W_0 = 10^{-12} \, W\)を取ります。
まとめ
本記事では、音の正体についておさらいし、音圧レベル、音響パワーレベルについて解説しました。
音圧レベルは、これまで工場や建設現場の騒音規制や自動車騒音の規格値(許容限度)などによく用いられてきましたが、近年では欧州や欧州の動向に倣った中国などで音響パワーレベルがよく用いられています。
これは、音圧レベルは測定する位置により変化するのに対し、音響パワーレベルは測定位置によらない普遍的な量となるためです。
下図に音圧\(p\)、音響インテンシティ\(I\)、音響パワー\(W\)の関係を図で示します。音圧は音源から離れるのに従って小さな値となります。

音響パワーの関係
最後に関連記事を紹介しておしまいとしたいと思います。





