物理現象を記述した方程式を支配方程式(または基礎方程式)と言います。
流体力学(Fluid mechanics)分野での支配方程式は連続の式、ナビエ・ストークス方程式、エネルギー方程式があります。
これらは質量保存則、運動量保存則、エネルギー保存則を式で表したものになります。
空気などの流体の流れをコンピュータ上で計算する際にはSTAR-CCM+などの流体解析ソフト(3D CAE)を使うことが多いですが、計算結果の妥当性を検証する際や計算結果のレビュー(DR)をする際に、基礎知識としてこれらの方程式を理解しておく必要があります。
また、MATLABなどを用いてイチから1Dモデルを作成する際にもこれらは理解しておく必要があります。
本記事では、エネルギー保存則(熱力学第一法則)を記述する式であるエネルギー方程式について解説し、1Dモデル作成時(モデルベース開発)の応用についても解説します。
エネルギー方程式

流体の性質と支配方程式
流体(Fluid)の性質を考えるとき、水やオイルなどの密度変化が小さいものと空気などの密度変化が大きいものを分けて考えると物理的性質を取り扱いやすくできる場合があります。
密度変化が小さいものに関しては、密度が変化しない「理想的な」流体と捉えて通常は問題を解きます。この密度が変化しない流体を非圧縮性流体と言います。
非圧縮性流体の流れを解くには、以下の支配方程式(基礎方程式)を満たす必要があります。
- 連続の式(質量保存則)
- ナビエ・ストークス方程式(運動量保存則)
一方、圧力や温度などによって比較的簡単に密度を変える空気に関しても、一般的な身の回りの流れにおいては大きな密度変化をしない場合が多いです。(風が吹いて窒息したって人は見たことありませんね。。。)
このような場合は、非圧縮性流体とみなして計算する場合が多いです。
しかし、音速と流速の比であるマッハ数が約0.3以上になると密度変化を無視できなくなってきます。このような場合は圧縮性流体として解くことになります。
この場合は変数として密度が増えるので、上記2つの支配方程式に加え、以下の支配方程式も加えた連立方程式を解く必要があります。
- エネルギー方程式(エネルギー保存則)
この式はエネルギー保存則、すなわち「熱力学第一法則」を記述する式になります。
次の項から具体的にエネルギー方程式について解説してきます。
熱力学第一法則について復習したい方は以下の記事を参考にしてみてね!
 熱と仕事(熱力学第一法則)
熱と仕事(熱力学第一法則)
流路でのエネルギーの関係
エネルギー方程式の導出にあたり、下図のような開いた系について考えてみましょう。
下図のように、ある時刻に管路に沿う2つ断面\(1\)と\(2\)の間に流体が満たされているものとします。この系は単位時間後に断面\(1’\)と\(2’\)で区切られた領域に移動し、単位時間当たり\(\dot Q \, (J/s)\)の熱量が加えられるものとします。
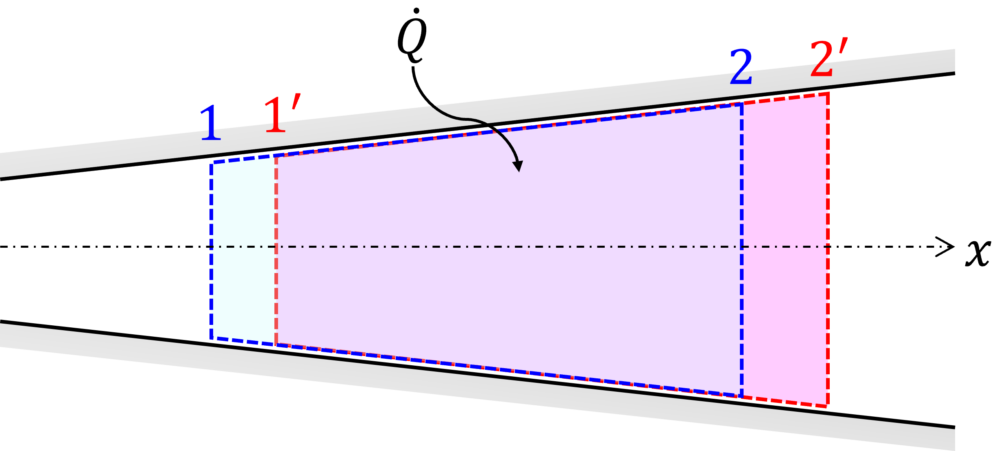
ここで、Fig.1の系は「開いた系の熱力学第一法則」より、下式のように表されます。
ここで、式(1)を単位質量あたりの熱量に書き換えてみましょう。
流体の密度を\(\rho \, (kg/m^3)\)、流路の断面積を\(A \, (m^2)\)、単位時間 かつ 単位質量当たりの熱量を\(\dot q \, (J/(kg \cdot s))\)と置くと、式(1)の左辺は以下のようになります。
密度\(\rho\)に体積\(A\, dx\)を掛けたものが質量になるね!
つぎに、系の内部におけるエネルギーの増加について考えましょう。
流れている流体は、内部エネルギー、運動エネルギー、位置エネルギーを持っています。このうち、位置エネルギーは気体の場合では他の2つに比べて十分小さいため、通常は無視できます。
空気などの流体は微視的にみると原子や分子で構成されているね。
微視的な立場での運動エネルギーの総和を内部エネルギーと呼ぶよ!
ここで、管内での流速を\(v \, (m/s)\)と置くと、単位質量当たりの運動エネルギーは\(v^2/2 \, (J/kg)\)となります。
よって、単位質量当たりの内部エネルギーを\(u \, (J/kg)\)と置くと、単位質量あたりの系の内部のエネルギーは\(u + v^2/2\)となります。
この系は\(x\)方向に移動するため、流体の運動に沿う微分(物質微分)\(D/Dt \)を用いると
となります。ここで、式(3)の右辺第一項は非定常項、右辺第二項と第三項は定常項を表しています。
右辺第二項は断面\(2\)から\(2’\)へ移動することによるエネルギーの増加、右辺第三項は断面\(1\)から\(1’\)へ移動することによるエネルギーの減少を示しているよ!
系が外部にする仕事として、機械的な仕事(工業仕事)や摩擦力による仕事(損失)はここでは無視し、流体が流れることによって行われる仕事である流動仕事\(W_f \, (J/s)\)について考えます。
流動仕事は、下図のような仮想的なピストンに置き換えて考えることができます。
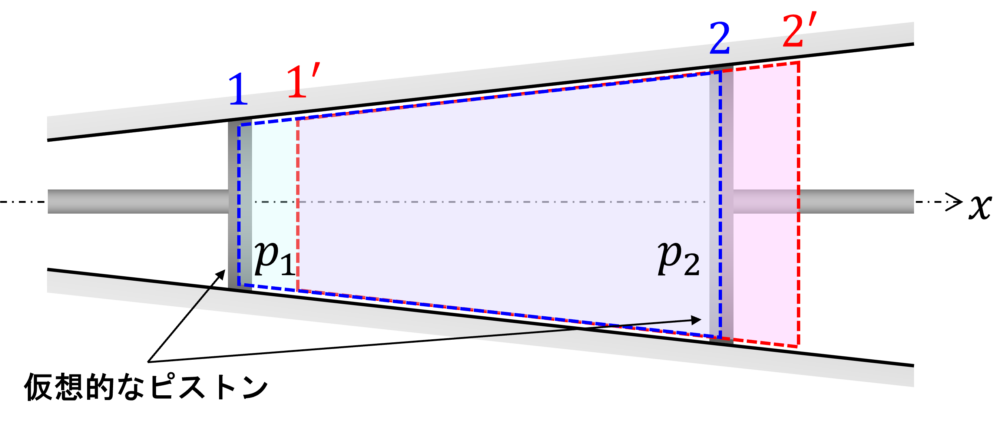
ここで、断面\(2\)から\(2’\)へ境界が移動するということは、系がピストンの圧力\(p_2\)に抗って境界面を押す仕事と同じになります。
よって、断面\(2\)での仮想的なピストンの力を\(F_2 \,(N)\)、ピストンの変位\(dx_2\)と置くと、仕事の定義より系が外部へする仕事\(W_{f2}\)は以下のようになります。
さらに、上式を単位時間あたりに直すと
となります。同様に断面\(1\)から断面\(1’\)へ境界が移動するということは、系が外部から\(p_1 A_1 v_1\)の仕事をされたことになります。よって、
\(\dot m \left( \frac{p_1}{\rho_1} \right)\)は断面\(1\)から流入するエネルギー、\(\dot m \left( \frac{p_2}{\rho_2} \right)\)は断面\(2\)から流出するエネルギーを示しているよ!
エネルギー方程式の導出
前項の式(1)に式(2)、(3)、(6)を代入すると下式になります。
上式を\(x\)で微分すると、微分形のエネルギー方程式となります。
ここで、断熱定常流れについて考えると、単位時間 かつ 単位質量当たりの熱量\(\dot q\)と非定常項である右辺第一項はゼロとなります。
さらに、その式を\(x\)について断面\(1\)から\(2\)まで積分し、連続の式(\(\rho_1 v_1 A_1 = \rho_2 v_2 A_2\))を用いると、
となります。上式は比エンタルピー(\(h \equiv u + p/\rho\))の定義より
と書き換えることができます。もし流れに沿って、全ての断面で平衡状態であれば下式が成り立ちます。
連続の式やナビエ・ストークス方程式について復習したい方は以下の記事を参考にしてみてね!
 流体力学「連続の式」ってなんだろう?
流体力学「連続の式」ってなんだろう?
 超・基礎から解説!ナビエ・ストークス方程式の導出【流体力学】
超・基礎から解説!ナビエ・ストークス方程式の導出【流体力学】
モデルベース開発(MBD)への応用

モデルベース開発(MBD)では、ある機能を持ついくつかのブロック(サブシステム)を接続し、対象製品のモデルを作成していきます。
熱力学における変数は圧力\(p\)、体積\(V\)、温度\(T\)の3つがありますが、真に独立なのは2つの変数になります。
よって、熱力学を基礎とした圧縮性流体のモデルを作成する際には、2つの変数を次のブロックに渡す必要があります。
また、ブロック(サブシステム)を作成する際には、将来の拡張性、メンテナス性などを確保するため、なるべく汎用的なモデル構造にする必要があります。
このため、ブロックの外部で単純に足し算できる状態量(スルー変数)にすることも重要です。
自動車メーカーとサプライヤが運営するMBD推進センター(JAMBE)が公開する「自動車開発におけるプラントモデル I/F ガイドライン」では、圧縮性流体(熱流体)を扱う場合、下表のようにスルー変数としてエンタルピー流量と質量流量を選ぶことを推奨しています。
| 物理領域 Domain | アクロス変数 (横断変数) | スルー変数 (流動変数) |
|---|---|---|
| 電気 Electrical | 電位・電圧 (Voltage) | 電流 (Current) |
| 並進運動 Translational | 速度 (Velocity) | 力 (Force) |
| 回転運動 Rotational | 角速度 (Angular velocity) | トルク (Torque) |
| 熱 Heat | 温度 (Temperature) | 熱流量 (Heat flow) |
| 非圧縮流体 Incompressible flow | 圧力 (Pressure) | 体積 流量 (Volume flow) |
| 熱流体 Thermal fluid | 温度 (Temperature) 圧力 (Pressure) | エンタルピー流量 (Enthalpy flow) 質量流量 (Mass flow) |
内部エネルギーや流動仕事に比べ、運動エネルギーが十分小さいとき(流速\(v\)が小さいとき)は式(11)より流体のもつエネルギーはエンタルピーが支配的になります。
よって、上表のようにエンタルピー流量を次のブロックに渡せばよいことになります。
一例としてエンジンシステムのモデル化の例を下図に示します。
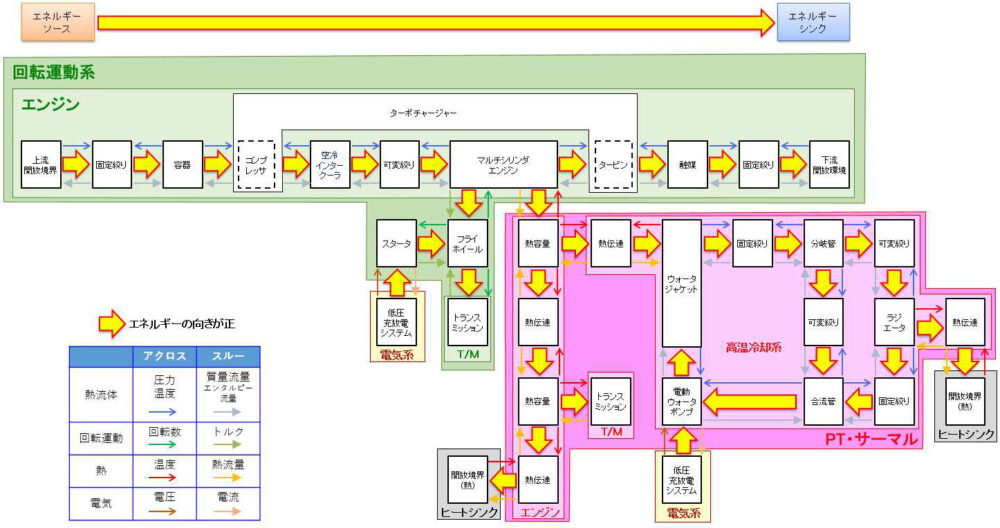
(引用元:AICE, エンジンシステムにおけるプラントモデルI/Fガイドライン)
モデル作成のガイドラインについて、詳しく知りたい方は以下の記事を参考にしてみてね!
 MBD(モデルベース開発)におけるプラントモデル I/F ガイドライン
MBD(モデルベース開発)におけるプラントモデル I/F ガイドライン

1Dモデルの基本的な考え方について学習されたい方は日本機械学会から発行されている以下の書籍が参考になりますね。
まとめ
非圧縮性流体の場合は、連続の式とナビエ・ストークス方程式を解くことで流れを解くことが出来ましたが、密度が変化する圧縮性流体の場合は、エネルギー方程式を解く必要があることを解説しました。
本記事では触れませんでしたが、管路の中の流れ(内部流れ)において入口の圧力を固定し、出口側の圧力を下げていくと通常は圧力差に連動する形で質量流量が増えますが、圧縮性流体ではある圧力まで下げたところで流量が一定となる現象があります。
これを窒息流(チョーク流れ)と言いますが、この現象を理解する際にもエネルギー方程式が必要となります。
一般的な流体力学の教科書(特に入門書)は非圧縮性流体がメインとなっていることが多いですが、圧縮性流体の全般的知識について学習されたい方は以下の書籍がおすすめです。
もし、内部流れに限定した形で深堀されたい方は以下の書籍が圧縮性流体の内部流れについて詳しく書かれた書籍としてはほぼ唯一になるかと思います。
少し高度にはなりますが、窒息流などの現象についても詳しく書かれており、大変勉強になるかと思います。



