モータの電気的時定数とは【電動化、1D CAE】

以前の記事にてDCモータが回転するメカニズムについて解説しました。

本記事ではモータの電気的時定数の意味について解説し、機械的時定数の導出についても解説していきます。

カヲル

機械的時定数に関してはこの記事を読んでね。

モータの機械的時定数とは【電動化、1D CAE】

電気的時定数とは

DCモータのシャフトを拘束（ロック）し、一定の電圧を印加すると電流が増加していき、やがて一定の電流になります。

電気的時定数（Electrical time constant）とは、電源ONから定常電流の63.2%に達するまでの時間のことです。

モータの巻線の電気抵抗を$R$（単位：$\Omega$）、インダクタンスを$L$（単位：$H$）と置くと、電気的時定数$\tau_E$（単位：$s$）は下式より求まります。

モータの電気的時定数

$$ \tau_E = \frac{L}{R} \tag{1} $$

電気的時定数の導出

まず、電圧$e_{mt}$（単位：$V$）を印加し、モータシャフトを拘束（ロック）させたときに電流$i$（単位：$A$）が流れる下図のようなDCモータのモデル（等価回路）を考えます。

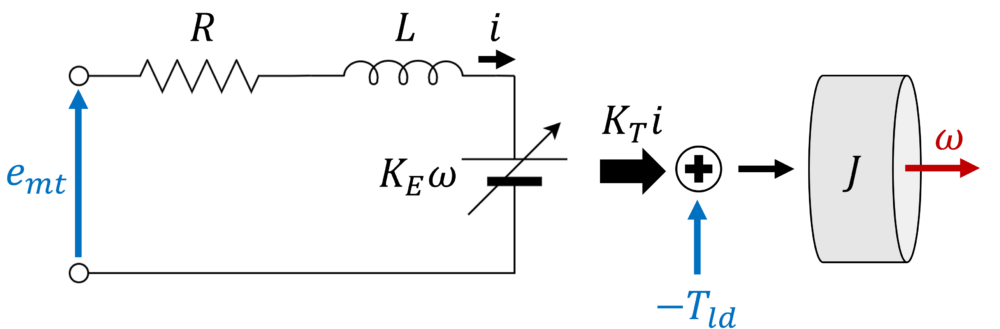
このとき、モータシャフトを拘束（$\omega = 0$）しているため、逆起電力は発生しません。よって、単純なRL直列回路について考えればよいことになります。

RL直列回路の数理式は以下のようになります。

$$ e_{mt} = R\,i + L \frac{di}{dt} \tag{2} $$

本記事では $t<0$ でモータに印加される電圧が $0$（$V$）だった状態が、$t \geq 0$ でモータに印加される電圧が $e_{mt}$（$V$）となるステップ入力での応答（ステップ応答）について考えます。

まず、式（２）を変数分離すると

$$ \begin{eqnarray} && e_{mt} \,-\, R\,i = L \frac{di}{dt} \tag{3}\\ \\ \rightarrow && \frac{1}{e_{mt} \,-\, R\,i} \, \frac{di}{dt} = \frac{1}{L} \tag{4}\\ \\ \rightarrow && \frac{1}{i \,-\, \displaystyle \frac{e_{mt}}{R}} \, \frac{di}{dt} = \,-\, \frac{R}{L} \tag{5} \\ \\ \rightarrow && \frac{1}{i \,-\, \displaystyle \frac{e_{mt}}{R}} \, di = \,-\, \frac{R}{L}\, dt \tag{6} \\ \end{eqnarray} $$

となり、両辺を積分すると以下のようになります。（$C_1$ は積分定数）

$$ \begin{eqnarray} && \int{\frac{1}{i \,-\, \displaystyle \frac{e_{mt}}{R}} } \, di = \int{\,-\, \frac{R}{L}}\, dt \tag{7} \\ \\ \rightarrow && \ln\left| i \,-\, \frac{e_{mt}}{R} \right| = \,-\, \frac{R}{L}t + C_1 \tag{8} \\ \end{eqnarray} $$

ここで指数をとると

$$ \left| i \,-\, \frac{e_{mt}}{R} \right| = \exp \left(\,-\, \frac{R}{L}t + C_1 \right) \tag{9} \\ $$

となります。左辺は全て正であるため、絶対値記号を外し、$\exp(C_1)$は定数であるため、$C_2$と置き換えると

$$ \begin{eqnarray} && i \,-\, \frac{e_{mt}}{R} = C_2 \exp \left(\,-\, \frac{R}{L}t \right) \tag{9} \\ \\ \rightarrow && i = \frac{e_{mt}}{R} + C_2 \exp \left(\,-\, \frac{R}{L}t \right) \tag{10} \\ \\ \end{eqnarray} $$

となります。ここで、$t=0$ のとき、$i=0$ という初期条件を与えると

$$ C_2 = \,-\,\frac{e_{mt}}{R} \tag{11} \\ $$

となります。式（１０）に式（１１）を代入し、式を整理すると以下のようになります。

モータのステップ応答

$$ i = \frac{e_{mt}}{R} \left[ 1 \,-\, \exp \left(\,-\, \frac{R}{L}t \right) \right] \tag{12} \\ $$

式（１２）の $\frac{L}{R}$ の部分は応答の速さを示し、電気的時定数と呼ばれます。